| Food description | Sodium | Potassium | Fat | Iron | Vitamin C | Folate | Carbohydrates |
|---|---|---|---|---|---|---|---|
| Bread, marble rye and pumpernickel, toasted | 663 | 182 | 3.63 | 3.11 | 0.4 | 103 | 53.08 |
| Cheese sandwich, Cheddar cheese, on white bread, with mayonnaise | 567 | 95 | 22.82 | 1.94 | 0.0 | 68 | 26.75 |
| Hamburger, 1 medium patty, with condiments, on bun, from fast food / restaurant | 374 | 225 | 11.60 | 1.73 | 0.3 | 22 | 22.14 |
| Herring, smoked, kippered | 918 | 447 | 12.37 | 1.51 | 1.0 | 14 | 0.00 |
| Ice cream sandwich, made with light chocolate ice cream | 55 | 185 | 6.60 | 0.93 | 0.9 | 7 | 38.54 |
| Oxtail soup | 139 | 105 | 4.87 | 1.12 | 1.9 | 6 | 1.37 |
| Pancakes, plain, reduced fat, from fozen | 667 | 171 | 9.54 | 1.51 | 0.0 | 46 | 36.09 |
| Pizza, cheese, with vegetables, from restaurant or fast food, medium crust | 535 | 171 | 8.69 | 2.26 | 4.8 | 85 | 30.71 |
| Rice, brown, with vegetables and gravy, NS as to fat added in cooking | 213 | 89 | 2.53 | 0.49 | 0.6 | 9 | 18.21 |
| Spinach, creamed, baby food, strained | 49 | 191 | 1.30 | 0.62 | 8.7 | 61 | 5.70 |
| Tomato rice soup, prepared with water | 319 | 129 | 1.06 | 0.31 | 5.8 | 6 | 8.54 |
| Tomato with corn and okra, cooked, made with butter | 323 | 154 | 2.48 | 0.39 | 10.1 | 26 | 6.72 |
| Tomato, green, pickled | 125 | 180 | 0.24 | 0.48 | 24.4 | 9 | 8.24 |
| Turkey with gravy, dressing, potatoes, vegetable, frozen meal | 326 | 230 | 3.89 | 0.79 | 0.8 | 24 | 16.32 |
| Vegetable combination, excluding carrots, broccoli, and dark-green leafy; cooked, no sauce, made with margarine | 275 | 163 | 2.06 | 0.71 | 12.7 | 32 | 11.99 |
6 Principal Component Analysis
This is a pre-release of the Open Access web version of Veridical Data Science. A print version of this book will be published by MIT Press in late 2024. This work and associated materials are subject to a Creative Commons CC-BY-NC-ND license.
Answering sophisticated domain questions often involves analyzing data that is high-dimensional, meaning that it contains a large number of variables. One example is biological gene expression data, which quantifies the extent to which each gene in the genome is being “expressed” and is particularly useful for answering questions about genetic traits that might be associated with disease. But since every person has more than 20,000 genes in their genome, every person’s gene expression data consists of more than 20,000 variables! How would you go about exploring the relationships and interactions between 20,000 variables at once? Unfortunately, most of the common visualization techniques (such as histograms and scatterplots) are designed to examine at most a few variables at a time and are certainly not suitable for visualizing the relationships between hundreds or thousands of variables at once. And it’s not just our visualization techniques that fail in the face of high-dimensional data. Many analytic techniques (such as predictive models) also perform poorly when there are too many variables, especially when there are not also large numbers of observations (and most of them fail entirely when there are more variables/columns than observations/rows).
In this chapter, we will introduce principal component analysis,1 a common approach for summarizing low-dimensional linear relationships in datasets whose size ranges from dimensions of around twenty or so variables to dimensions of hundreds of thousands of variables. Regardless of the dimension of the data, if a few low-dimensional linear summaries of the data can effectively capture the majority of the original “variation” in the data, then they can be used to create a simplified version of the data that has substantially fewer variables while retaining most of the information of the original dataset. Armed with a simplified lower-dimensional version of our data, we can apply our favorite visualization techniques (and predictive models) to tease out the patterns hidden within. Note that principal component analysis has had a long history in statistics, originally introduced in 1901 by Karl Pearson (Pearson 1901), and later independently invented (and named) by Harold Hotelling (Hotelling 1933).
The process of creating a lower-dimensional representation of a dataset is generally known as dimensionality reduction. The goals of dimensionality reduction are to better understand and summarize the strongest patterns and relationships between the variables in the data (i.e., the intrinsic structure of the data), and/or to make computation on the data easier by reducing its size.
In this chapter, we will use principal component analysis to summarize the linear relationships between the variables of a dataset. In Chapter 7, we will introduce the technique of clustering, which instead aims to summarize the relationships between the observations (rather than the variables) of a dataset. The principal component analysis algorithm that we will introduce in this chapter—as well as the clustering algorithms that we will introduce in the next chapter—fall under the umbrella of unsupervised learning algorithms, a branch of machine learning (ML). However, these techniques were in use long before the arrival of the modern field of ML.
Note that for data science projects whose overall goal is not necessarily to summarize the relationships between the variables or observations, these analyses are not a required step of the data science life cycle (DSLC). However, using these techniques to develop an understanding of the intrinsic structure of your data can be a powerful exploratory exercise, helping to uncover useful patterns and relationships that would otherwise remain hidden (even if you don’t use the resulting simplified, lower-dimensional summaries in your downstream analyses).
At the end of this chapter, we will demonstrate how to evaluate the trustworthiness of your principal component analysis using the principles of predictability, computability, and stability (PCS).
6.1 The Nutrition Project
In this chapter, we will demonstrate the techniques of dimensionality reduction in the context of a project whose goal is to produce a summary of the intrinsic structure of a dataset. We will place ourselves in the role of someone who wants to develop an app that can provide users with simplified nutritional summaries of their meals. While the typical user of this app will probably know about nutrients such as fat and vitamin C, they probably won’t have a particularly deep understanding of the dozens of the other common nutrients that are measured in our food, such as thiamine, arachidonic acid, or phosphorus. Our goal for this chapter is to reduce this complex list of nutrient measurements into just a few interpretable “summary nutrients” (such as “Vitamins,” “Minerals,” “Fats,” etc.) that can provide a general sense of how balanced a meal is in terms of the different types of nutrients (without having to understand the nuances in the long and complex list of specific individual nutrients). With this simplified nutrition information, users will hopefully be able to make healthier eating decisions that will better cater to their nutritional needs.
6.1.1 Data Source
The data that we will use for this project comes from the US Department of Agriculture’s (USDA) Food and Nutrient Database for Dietary Studies (FNDDS) (Fukagawa et al. 2022), which contains nutrient information compiled for the foods and beverages reported in the “What We Eat in America” survey. This data contains 8,690 food items such as a bacon and cheese sandwich, honeydew melon, and carbonara pasta.
Each food item has measurements for 57 nutrients (variables), including iron, carbohydrates, fat, thiamine, and riboflavin. Table 6.1 displays a random sample of 15 food items, along with the measurements recorded for 7 of the 57 nutrients.
Since this is a public dataset and we are not in contact with the people who collected it, we tried to learn as much about the data as possible from the information provided online.2 While conducting step 1 of the data cleaning procedure (“learn about the data collection process and the problem domain”) from Chapter 4, several questions quickly arose, such as “What scale are the nutrient measurements for each food item on, and are they comparable?” If the data contains entries for both an entire pizza and a chocolate bar, do the nutritional measurements correspond to the entire food item, or for comparable amounts of each item (e.g., 100 g of each)? Fortunately, the documentation provided for the FNDDS database specifies that each of the nutrient amounts are based on 100 g of the food item, so the nutritional contents reported for different foods should be comparable (akin to comparing donation rates per million, rather than the raw donation counts across different countries in Chapter 5).
Next, we wanted to understand how the nutrition values in the data were measured. By reading the available data documentation and by conducting a literature review, we learned that different nutrients are measured using various scientific methods, ranging from measuring the food’s light reflectance spectrum to computing the amount of weight the food item lost after being microwaved (Noh et al. 2020). Since we can pretty much guarantee that no one took the time to shoot fancy light beams at your premade pasta carbonara, the nutritional information reported on its label was most likely estimated based on preexisting data on the nutritional content of its labeled ingredients.
How reliable are these estimation methods? Do you think that the reported nutritional values perfectly correspond to the actual nutritional content? In our literature search, we encountered a study asking this exact question (Jumpertz et al. 2013), which identified discrepancies in the reported nutritional measurements and their own experiments measuring the nutrient content of many common snack foods. The study found, when focusing on discrepancies in reported and measured calories, that “most products in our sample fell within the allowable limit of 20 percent over the label calories per Food and Drug Administration (FDA) regulations.” They also found that “carbohydrate content exceeded label statements by 7.7 percent” and that “fat and protein content were not significantly different from label statements.” This information will be helpful when it comes time to investigate the stability of our eventual results to appropriate data perturbations.
A more detailed discussion of the data and the background domain can be found in the files in the nutrition/dslc_documentation/ folder in the supplementary GitHub repository.
6.1.2 A Predictability Evaluation Plan: The Legacy Dataset
Before we get started exploring the data, we need to make a plan for how to evaluate the predictability of our downstream results. Fortunately, the USDA also provides us with several other nutrient datasets (each based on different nutrient measurement techniques and containing many similar food items) that we can use to evaluate the predictability of our results. We chose to use the “SR Legacy” (Legacy) dataset for our predictability evaluations. The Legacy dataset has been the primary food composition dataset in the US for decades and has the most overlap in nutrients with the FNDDS dataset. Most importantly, of all the datasets available, the food items measured in the Legacy dataset most closely resemble the kind of food items that the hypothetical users of our app would be interested in. This additional Legacy dataset contains 7,793 food items and 135 nutrients (including all 57 nutrients from the FNDDS data). Our plan is thus to develop our results using the FNDDS dataset and evaluate them using the Legacy dataset.
As a brief reality check that the two datasets are reasonably similar to one another, Table 6.2 shows the nutrition information from two similar food items from each dataset: lowfat plain yogurt and canned minestrone soup. The yogurts appear to be identical, whereas the soups have similar—but not identical—nutrition information. For more comparisons of the two datasets, see the relevant data cleaning and exploratory data analysis (EDA) code files (01_cleaning.qmd and 02_eda.qmd, or equivalent .ipynb files, in the nutrition/dslc_documentation/ subfolder) in the supplementary GitHub repository.
| Food description | Dataset | Sodium | Potassium | Fat | Iron | Vitamin C | Folate | Carbohydrates |
|---|---|---|---|---|---|---|---|---|
| (a) Yogurt, Greek, low fat milk, plain | FNDDS | 34 | 141 | 1.92 | 0.04 | 0.8 | 12 | 3.94 |
| (a) Yogurt, Greek, plain, lowfat | Legacy | 34 | 141 | 1.92 | 0.04 | 0.8 | 12 | 3.94 |
| (b) Minestrone soup, canned, prepared with water, or ready-to-serve | FNDDS | 261 | 128 | 1.03 | 0.38 | 0.5 | 15 | 4.60 |
| (b) Soup, minestrone, canned, chunky, ready-to-serve | Legacy | 288 | 255 | 1.17 | 0.74 | 2.0 | 22 | 8.64 |
6.1.3 Data Cleaning
The FNNDS data came spread across several separate files that we had to join together using key ID variables (although we had to manually convert the nutrient ID variables to nutrient names since the formatting of many of the nutrient names was inconsistent, misspelled, and/or repetitious). Fortunately, however, the data did not seem to contain any missing or invalid values. Our full data cleaning process can be found in the 01_cleaning.qmd (or .ipynb) file in the nutrition/dslc_documentation/ subfolder of the online GitHub repository.
6.1.4 Exploratory Data Analysis
Figure 6.1 displays a heatmap of the entire FNDDS dataset (the rows correspond to the 8,690 food items). Since the range of each nutrient variable is quite different, we standardized the nutrients (by subtracting the mean and dividing by the standard deviation) within each column of the heatmap to help with comparability (recall Section 5.3 in Chapter 5). We will discuss this standardization technique (a preprocessing task) in Section 6.3. Note that we arranged and grouped the nutrients/columns in Figure 6.1 so that related nutrients are grouped together (where the judgment call that nutrients that are “related” to one another is based on both the data and domain knowledge). Note that these groupings will play a significant role in our analysis of this data, as we will discuss in the next section. A more detailed EDA can be found in the 02_eda.qmd (or .ipynb) file in the nutrition/dslc_documentation/ subfolder of the online GitHub repository.
6.1.5 The Analysis Plan: Summarizing Nutrient Groups Separately
Recall that our goal for this chapter is to create a small number of informative summary nutrient variables. Each summary nutrient variable should summarize the information contained within a collection of related nutrients. For example, our goal is to create a single “vitamin” summary nutrient variable (that summarizes the information from the vitamin C, vitamin B6, beta carotene, and other vitamin variables), a single “trace mineral” summary nutrient variable (that summarizes the information from the zinc, copper, magnesium, and other trace mineral variables), and so on.
After applying the principal component analysis dimensionality reduction algorithm that we will introduce in this chapter to the whole dataset, it quickly became clear that the algorithm is not capable of automatically creating meaningfully distinct nutrient summaries (such as “vitamins,” “trace minerals,” “fats,” etc.) without manual intervention. We thus decided to first manually divide the data into distinct datasets—one for each of the specific nutrient groups we wish to summarize—and to apply the dimensionality reduction technique separately to each nutrient group dataset.
Using a combination of domain knowledge (from domain literature, as well as our own understanding of which nutrients are related to one another) and data explorations, we created the following nutrient groups:
Vitamins: Vitamin C, vitamin B6, vitamin B12, riboflavin, thiamine, folate, niacin, beta carotene, alpha carotene, lutein zeaxanthin, phylloquinone, alpha tocopherol, retinol, lycopene, and cryptoxanthin
Fats: Fat, saturated fat, monounsaturated fat, polyunsaturated fat, cholesterol, and all the fatty acids
Major minerals: Sodium, potassium, calcium, phosphorus, magnesium, and total choline
Trace minerals: Iron, zinc, selenium, and copper
Carbohydrates: Carbohydrates and total dietary fiber
Calories: Calories
Protein: Protein
These nutrient groups are the same as those shown in the heatmap in Figure 6.1.
Since the “Calories” and “Protein” nutrient groups contain only one nutrient each, we don’t need to further summarize them.3 Note that we have made several judgment calls when deciding how to define these groups. For example, alternative judgment calls might involve combining the “Minerals” and “Trace minerals” nutrient groups or creating separate groups of “Saturated fat” nutrients and “Unsaturated fat” nutrients.
Since we will be using this food dataset throughout this (and the next) chapter, if you’re coding along yourself, we suggest working through the 01_cleaning.qmd and 02_eda.qmd (or .ipynb) files in the nutrition/dslc_documentation/ subfolder in the supplementary GitHub repository and adding your own explorations to them too. An example of an additional exploratory question that you could ask is: Which nutrients are most highly correlated with one another?
Although our goal is to compute a separate summary of each of these nutrient groups, to simplify our introduction of principal component analysis, we will first focus our analysis on just the “Major minerals” nutrient group, which contains sodium, potassium, calcium, phosphorus, magnesium, and total choline.
6.2 Generating Summary Variables: Principal Component Analysis
Our initial goal is to identify and summarize the strongest linear relationships among the “Major mineral” nutrient group variables, which correspond to sodium, potassium, calcium, phosphorus, magnesium, and total choline. Later, we will also apply the same analysis to the other nutrient groups (“Fats,” “Vitamins,” “Trace minerals,” etc).
To help you understand the kind of linear summaries that we will be exploring in this chapter, let’s consider an example of the simplest linear summary of the 6 “Major mineral” nutrients that we could compute, corresponding to an unweighted sum (linear combination) of their values:
\[\textrm{sodium} + \textrm{potass.} + \textrm{calcium} + \textrm{phosph.}+ \textrm{magnes.}+ \textrm{total choline}.\]
If we were to replace the original “Major mineral” dataset (which consists of the six “Major mineral” nutrient variables) with just a single variable corresponding to their sum, then we would have reduced the dimension of the data from six down to just one!
However, a natural concern is whether this unweighted linear combination represents a good summary of the six original “Major mineral” nutrients. How much information are we losing by replacing the six variables with their sum? Can we come up with a better summary, which captures more of the original information in the data? For example, if some of the individual nutrient variables were more important than the others, might we be able to compute a more informative summary by allowing the more important variables to contribute more to the sum than the less important ones?
One way to alter the influence of each variable within a linear combination is to add a weight in the form of a coefficient (a multiplier) to each variable in the sum. The size of each variable’s coefficient determines how much it contributes to the summation (but only if each of the original variables are on the same scale). More important variables should be given larger coefficients, and less important variables should be given smaller ones. For example, if phosphorus was the most important variable, followed by potassium, sodium, calcium, total choline, and then magnesium, we could capture these importance rankings using the following weighted linear combination:
\[ \begin{align*} 4\textrm{sodium} + 5 \textrm{potass.} + 3 \textrm{calcium} + 6 \textrm{phosph.} + \textrm{magnes.} + 2 \textrm{tot. choline}. \end{align*} \]
How do we know which variables/features are the most important ones? And how should we decide the size of each coefficient? What is the best linear combination of our features? The answer to that question will depend on how we choose to define “best.”
In this chapter, we will define the best possible linear combination as the one that best captures the variation in the original data.4 Recall that the variance of a variable conveys how spread out its values are. Another way to think about the variance of a variable is as a measure of how well the variable’s measurements can distinguish between the observations. Our goal is thus to identify a linear combination of the “Major mineral” nutrient variables whose values exhibit maximum variation (i.e., are most able to distinguish between the individual observations). The algorithm we will use to achieve this goal is called principal component analysis.
Principal component analysis is an algorithm that computes a series of “orthogonal” linear combinations that have the maximum possible variance relative to the origin5 (the data point whose measurements across all variables equal zero). As an example, let’s consider the two-dimensional example dataset that contains just the sodium and potassium variables. Note that we are considering just two dimensions here so that we can visualize principal component analysis using a scatterplot. To keep our explanations as simple as possible, we will consider a version of this data that has been standardized (i.e., where each variable has been mean-centered and scaled/divided by its standard deviation). We will discuss standardization in Section 6.3. Whether to standardize your data in practice is a preprocessing judgment call that should be based on domain knowledge.
Figure 6.2 presents a scatterplot of the 15 food items from Table 6.1 in the two-dimensional sodium and potassium subspace, and it displays a line (passing through the origin) that represents one possible summary of the linear relationship (the linear trend) between these two variables. If this line was perfectly diagonal, then both the sodium and potassium variables would have equal importance in the summary (i.e., they would have the same coefficient/weight in the formula that defines this linear summary). As the angle of the line shifts, it places more or less weight on each variable.
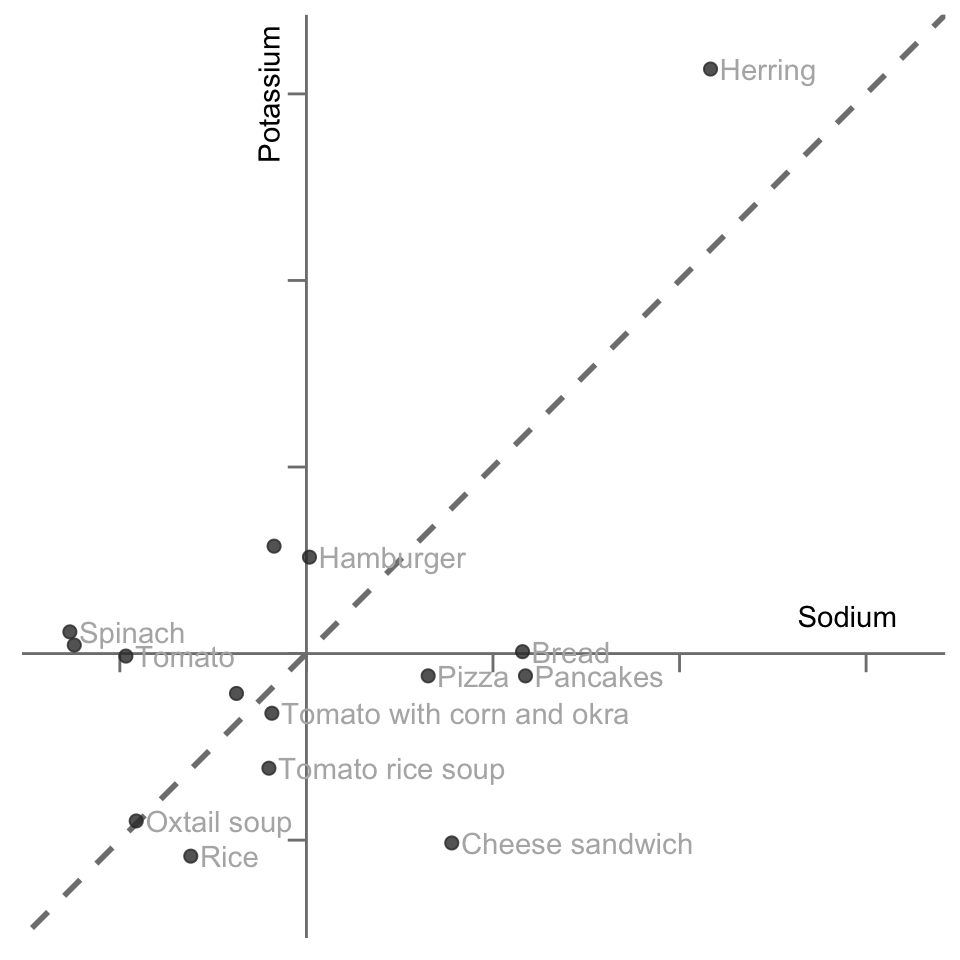
6.2.1 The First Principal Component
There are many possible lines that we could have placed in Figure 6.2 that might be perceived as “capturing” the linear relationship between sodium and potassium for these 15 food items. The question is: What line will capture the most variability in the data? The line that we’re looking for will be the line along which the projected data points exhibit the most variation (i.e., the projected points are the most spread out along the line).
Let’s unpack this a bit. The projection of a data point onto a line is the position on the line that is closest to the data point (in the case of this two-dimensional example, the definition of “distance” we are using is the perpendicular distance from the point to the line). Figure 6.3 shows the projection of each data point onto the line. By treating the projected position (the orange points) of each data point on our summary line as a measurement, the linear combination that corresponds to the line can be thought of as a summary variable that summarizes the two original variables.
Figure 6.4 shows the summary line as a variable (we just rotated the summary line so it is horizontal). Try to match up the orange projected data points along the diagonal summary line in Figure 6.3 with the orange points along the horizontal line in Figure 6.4.
The line along which the orange projected data points exhibit maximal variation6 is called the first principal component (PC) (Box 6.2). It turns out that another definition of the first principal component is as the line for which the average perpendicular (projection) distance from each data point to the line is minimized.
While this first principal component captures the strongest linear relationship in the data (that which lies in the direction of greatest variation), datasets with many variables often contain multiple distinct linear relationships, each involving different combinations of the variables. Fortunately, we can compute multiple principal components, each designed to capture a direction of variation that was not captured by the previous principal components.
If the first principal component is the line along which the projected data points exhibit the greatest variation, the second principal component is the line, orthogonal to the first, along which the projected data points exhibit the next greatest variation. In two dimensions, “orthogonal” is the same as “perpendicular,” which means that there is a 90-degree right angle between the two lines. For instance, in two dimensions, the \(x\)- and \(y\)-axes are orthogonal to one another, and in three dimensions, the \(x\)-, \(y\)-, and \(z\)-axes are all orthogonal to one another.
The second principal component for the 15 data point sodium-potassium example is shown in Figure 6.5 as a dotted line (the original “first” principal component is shown as a dashed line). The purple points correspond to the projections of each data point onto this second principal component.
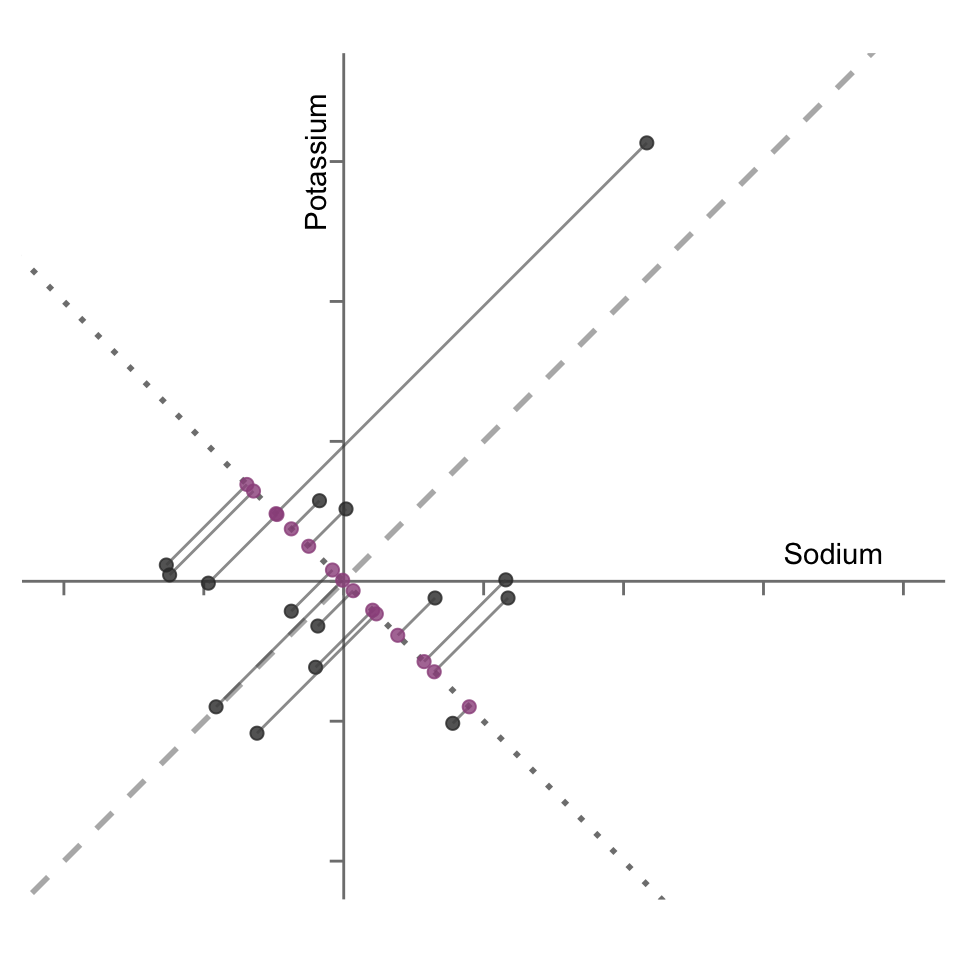
By nature of the first principal component being the line along which the projected data points exhibit the greatest variation, the data points projected onto the second principal component are necessarily less variable than their projections onto the first principal component. For evidence of this fact, notice that the projections of the data points onto this second principal component (shown in Figure 6.5) are less spread out compared with the projections onto the first principal component (which were shown in Figure 6.3).
If there is a second principal component, does this also mean that there can be a third? Yes, it does! You can calculate as many principal components as there are original dimensions in your data. So in the six-dimensional “Major minerals” subset of our nutrient dataset, we can create up to six principal components. The process of computing principal components is called principal component analysis. The first principal component will capture the most variation in the data, followed by the second principal component, followed by the third principal component, and so on. Each principal component must be orthogonal to one another. Taking just a few of these principal components (e.g., using each principal component linear combination as a new variable), you can create a lower-dimensional representation of your data that still contains much of its original variation.
Before we describe how to compute the principal components (using a linear algebra technique called “singular value decomposition”), let’s first have a discussion about standardization as a preprocessing step for principal component analysis.
6.3 Preprocessing: Standardization for Comparability
The most common preprocessing step for principal component analysis is standardization, which involves both mean-centering (subtracting the mean from each column) and SD-scaling (dividing each column by its standard deviation (SD)). However, neither of these steps are actually required for principal component analysis, and while they will be sensible preprocessing steps for some data science projects, they won’t be for others. Whether it makes sense to mean-center and/or SD-scale your variables before conducting principal component analysis will depend on what the numbers in your data mean. For instance, the decision to SD-scale your data will depend on whether your variables are already on a common scale, and the decision to mean-center your data will depend on whether a value of 0 is meaningful (e.g., if the measurements are counts relative to 0, then it may not make sense to mean-center them).
Let’s first talk about SD-scaling the data by dividing each variable by its standard deviation. Principal component analysis works by computing the direction of maximum variation. However, variance computations will yield larger variance values for variables that contain larger numbers and smaller variance values for variables that contain smaller numbers. This can unintentionally give the impression that variables of larger magnitudes contain more variable information than those of smaller magnitudes. Therefore, if your variables have very different scales/magnitudes, it is often a good idea to convert them to a common scale by SD-scaling them (\(\frac{x}{\textrm{SD}(x)}\)) or by transforming them to a common range (such as a range of [0, 1], using \(\frac{x - \min(x)}{\max(x) - \min(x)}\)). This will ensure that it is the actual variability of the information contained in each variable that dictates these variance computations rather than the variable’s relative magnitudes/scales.
However, there will be some situations in which the relative scale of the variables is meaningful, and scaling them will remove this meaning. For instance, if each variable always takes a number between 1 and 10, but some variables just happen not to span the whole spectrum of possible values, rescaling the variables may be misleading since it will remove the information captured by the fact that some variables are inherently not covering their entire possible range. In the case of our nutrient dataset, however, the measurements for each nutrient have their own scale, and there is no particular meaning behind the fact that magnesium typically has values in the tens, while sodium’s values are often in the hundreds. Thus, we deem that it is sensible to SD-scale each of our nutrient variables.
What about mean-centering? Recall that principal component analysis identifies the direction of maximum variation, where this variation is considered relative to the origin. If your data has been mean-centered, then this origin actually corresponds to the original mean of the data values, so the “variation relative to the origin” corresponds to the traditional definition of variation (i.e., \(\sum_i (x_i - \bar{x})^2\)). If, on the other hand, your data has not been mean-centered, this variation is relative to the zero data point (i.e., \(\sum_i (x_i - 0)^2\)). Note, however, that the latter approach (computing the direction of maximum variation relative to the zero data point) only really makes sense when the value 0 holds meaning (e.g., each measurement is a positive count relative to zero).
Do you think that we should mean-center our nutrient data? Should the variation in each of the nutrient variables be interpreted relative to 0 or their mean? Since each nutrient variable measures how much of the nutrient is in the food item, with the smallest amount being 0, it makes sense to interpret the variation in each variable relative to 0, indicating that mean-centering may not be necessary for this particular dataset. Keep in mind that your choice of whether to mean-center your data will affect the interpretation of the principal components that you produce in terms of whether the variation they are capturing is relative to the zero data point or the average data point.
If you aren’t sure whether to SD-scale and/or mean-center your data, you can investigate whether the judgment call you make affects your results by conducting a PCS evaluation.
Note, however, that it is more common in practice to apply principal component analysis to mean-centered data.
6.4 Singular Value Decomposition
Warning: this section is going to be a bit more technical and will require some knowledge of linear algebra.
Principal components are typically computed using a canonical linear algebra matrix decomposition technique called singular value decomposition (SVD).7 SVD decomposes a matrix (numeric dataset) into its core mathematical components. Note that since SVD can be applied only to numeric datasets, any categorical variables need to be converted to numeric formats during preprocessing (we will discuss such categorical-to-numeric one-hot encoding conversions in Chapter 10). However, note that while you can technically apply SVD to numeric data with binary or integer-valued numeric variables, it is actually designed for continuous numeric values. You can apply SVD to a matrix in R using the svd() function. In Python, you can use the linalg.svd() function from the Numpy library.
While we will use SVD to perform principal component analysis, an alternative approach involves implementing a related technique called eigendecomposition. Eigendecomposition decomposes the covariance matrix of a dataset, rather than the original data matrix itself. If the data has been mean-centered, then these two approaches (eigendecomposition of the covariance matrix and SVD of the original data matrix) are the same.8 The reason that we use SVD rather than eigendecomposition to introduce the principal component analysis algorithm is that SVD is more useful in practice (eigendecomposition can only be applied to symmetric matrices, whereas SVD can be applied to any matrix) as well as more computationally efficient and stable.
SVD works by decomposing a data matrix into the product of three matrices as follows:
\[ X = U D V^T. \tag{6.1}\]
The matrices U and V contain orthonormal (i.e., orthogonal and unit length) columns and each column contains information on the direction of a principal component. The matrix \(D\) is a diagonal matrix (meaning that all the “off-diagonal” entries are 0) whose diagonal entries correspond to the magnitude or strength of the corresponding principal component directions. Figure 6.6 provides some intuition: imagine overlaying a unit circle over some data that lives in a two-dimensional space with horizontal and vertical axes. Our goal is to transform this unit circle (whose axes correspond to the original \(x\)- and \(y\)-axes) into an oval whose axes represent the first two principal components.
When the matrix representing the unit circle is multiplied9 by the matrix \(V^T\) (the first transition in Figure 6.6), the unit circle is rotated so that its axes now face in the direction of the principal components (i.e., the strongest directions of variation of the data). Notice how one of the circle’s unit axis arrows is now pointing in the primary direction along which the data seems to spread (and the other is perpendicular to it). Next, we want to stretch/extend each of the circle’s unit axis arrows to represent the magnitude of variation in each direction. We can do this by multiplying this rotated unit circle by the diagonal matrix \(D\) (the second transition in Figure 6.6) so that the circle’s axes better fit the shape of the data. The larger the relevant value in \(D\), the more the corresponding axis is stretched.
The first column of \(V\) and the first diagonal entry of \(D\) together correspond to the direction and magnitude of the first principal component; the second column of \(V\) and the second diagonal entry of \(D\) correspond to the direction and magnitude of the second principal component; and so on. In the context of SVD, the columns of \(V\) are called the right-singular vectors of the data matrix and each right-singular vector corresponds to a principal component. Each column of \(V\) contains the coefficients of the corresponding principal component linear combination. These coefficients are also known as the variable loadings (Box 6.3) for the relevant principal component. Note that the left matrix, \(U\), contains the left-singular vectors (but we are not particularly interested in \(U\) in principal component analysis).
The code for computing the SVD of the “Major minerals” dataset can be found in the 03_analysis_pca.qmd (or .ipynb) file in the nutrition/dslc_documentation/ subfolder of the supplementary GitHub repository.
The right-singular vector matrix, \(V\), for the “Major mineral” nutrient training data example (based on all the FNDDS food items) is as follows:10
\[\begin{equation*} V = \overset{~~~~~~~~~~~~~~~~~~~\textrm{(PC1)}~~~~\textrm{(PC2)}~~~~\textrm{(PC3)}~~~~\textrm{(PC4)}~~~~\textrm{(PC5)}~~~~\textrm{(PC6)}}{\begin{array}{r} \textrm{(Sodium)} \\ \textrm{(Potassium)} \\ \textrm{(Calcium)} \\ \textrm{(Phosphorus)} \\ \textrm{(Magnesium)} \\ \textrm{(Total choline)} \\ \end{array}\left[ \begin{array}{rrrrrr} 0.42 & 0.63 & 0.23 & -0.58 & 0.15 & -0.1\\ 0.48 & -0.28 & -0.43 & -0.3 & -0.64 & 0.1\\ 0.29 & -0.24 & 0.79 & 0.22 & -0.35 & -0.27\\ 0.49 & -0.06 & 0.12 & 0.28 & 0.3 & 0.76\\ 0.38 & -0.51 & -0.16 & -0.11 & 0.59 & -0.46\\ 0.35 & 0.45 & -0.33 & 0.66 & -0.08 & -0.35\\ \end{array}\right]}. \end{equation*}\]
Based on the entries of the first column of \(V\), the first principal component can be written as the following linear combination of the “Major mineral” variables:
\[ \begin{align} \textrm{PC1} =~& 0.42 \textrm{ sodium} ~+~ 0.48 \textrm{ potassium} ~+~0.29 \textrm{ calcium} \nonumber\\ &~+~ 0.49 \textrm{ phosphorus} ~+~0.38 \textrm{ magnesium} \nonumber\\ &~+~0.35 \textrm{ total choline}. \end{align} \tag{6.2}\]
Which variables appear to be driving the first principal component? Since phosphorus and potassium have the largest variable loadings (in absolute value), they contribute the most to this first principal component. Note that these coefficients are only comparable because we SD-scaled each of our variables before performing SVD. However, since the coefficients are all fairly similar, this first principal component seems to be a fairly equal summary of all the “Major mineral” nutrients.
If the second and third columns of \(V\) define the second and third principal components, respectively, as an exercise, write the linear combinations that define the second and third principal components and provide a short summary of which variables are most contributing to the second and third principal components. Note that it is the absolute value magnitude of the loading that determines the importance of each variable.
Table 6.3 shows each of the SD-scaled “Major mineral” nutrient variable values for the “Herring, smoked, kippered” food item.
| Sodium | Potass. | Calc. | Phosp. | Magn. | Chol. |
|---|---|---|---|---|---|
| 2.87 | 2.3 | 0.75 | 2.71 | 1.29 | 2.34 |
To compute the value of the first principal component for a food item, such as for the “Herring” food item shown in Table 6.3, you can plug the relevant (SD-scaled) nutrient variable values into the first principal component linear combination from Equation 6.2:
\[\begin{align*} \textrm{PC1(herring)} =&~ 0.42 \times 2.87~+~ 0.48 \times 2.3~+~ 0.29 \times 0.75 \\ &~+~ 0.49 \times 2.71 ~+~0.38 \times 1.29 ~+~ 0.35 \times 2.34 \\ =&~ 5.164. \end{align*}\]
To create a lower-dimensional dataset based on the principal components, you need to compute the relevant principal component values (as we did for “Herring, smoked, kippered”) for each food item. Fortunately, you don’t need to do this manually. Efficient computation of the principal component variables for all food items at once can be done using matrix multiplication. If \(X\) is the original dataset and \(V\) is the right-singular vector matrix (containing the relevant principal component coefficients), then the Principal Component dataset, which we denote as \(X^{PC}\), can be computed via the matrix multiplication of \(X\) and \(V\):
\[ X^{PC} = XV. \tag{6.3}\]
If we want to reduce the dimension of the “Major minerals” dataset from six to just three, we can create a dataset that consists of just the first three principal component values for each food item.
For our sample of 15 food items, the first three principal component variables based on the “Major minerals” dataset are shown in Table 6.4 (although we are just showing the principal component data for the sample of 15 food items here, the principal components were computed based on the SVD of the entire “Major minerals” FNDDS dataset).
| Food description | PC1 | PC2 | PC3 |
|---|---|---|---|
| Bread, marble rye and pumpernickel, toasted | 4.62 | -0.19 | -0.92 |
| Cheese sandwich, Cheddar cheese, on white bread, with mayonnaise | 4.24 | 2.84 | -0.93 |
| Hamburger, 1 medium patty, with condiments, on bun, from fast food / restaurant | 4.03 | -0.37 | 0.15 |
| Herring, smoked, kippered | 8.72 | -0.97 | 1.72 |
| Ice cream sandwich, made with light chocolate ice cream | 3.06 | -0.30 | -0.91 |
| Oxtail soup | 1.97 | -0.41 | 0.66 |
| Pancakes, plain, reduced fat, from fozen | 5.30 | 1.97 | 0.72 |
| Pizza, cheese, with vegetables, from restaurant or fast food, medium crust | 4.15 | 1.08 | -0.31 |
| Rice, brown, with vegetables and gravy, NS as to fat added in cooking | 2.22 | -0.53 | -0.64 |
| Spinach, creamed, baby food, strained | 3.75 | -1.37 | -2.27 |
| Tomato rice soup, prepared with water | 1.64 | -0.32 | 0.58 |
| Tomato with corn and okra, cooked, made with butter | 2.48 | -0.56 | -0.18 |
| Tomato, green, pickled | 1.95 | -0.89 | 0.06 |
| Turkey with gravy, dressing, potatoes, vegetable, frozen meal | 3.34 | -0.76 | 0.28 |
| Vegetable combination, excluding carrots, broccoli, and dark-green leafy; cooked, no sauce, made with margarine | 2.63 | -0.73 | 0.00 |
Having computed the “Major minerals” principal component variables for each food item, we can visualize the food items in principal component space. Figure 6.7(a) and (b) display scatterplots of 500 of the FNDDS food items in the space defined by the first two principal components, and the second and third principal components, respectively. Some individual food items are annotated in each plot (note that we have used subsampling and transparency to reduce overplotting). It is encouraging to see that similar food items appear near each other in each principal component scatterplot (based on our subjective opinion of which food items are similar).
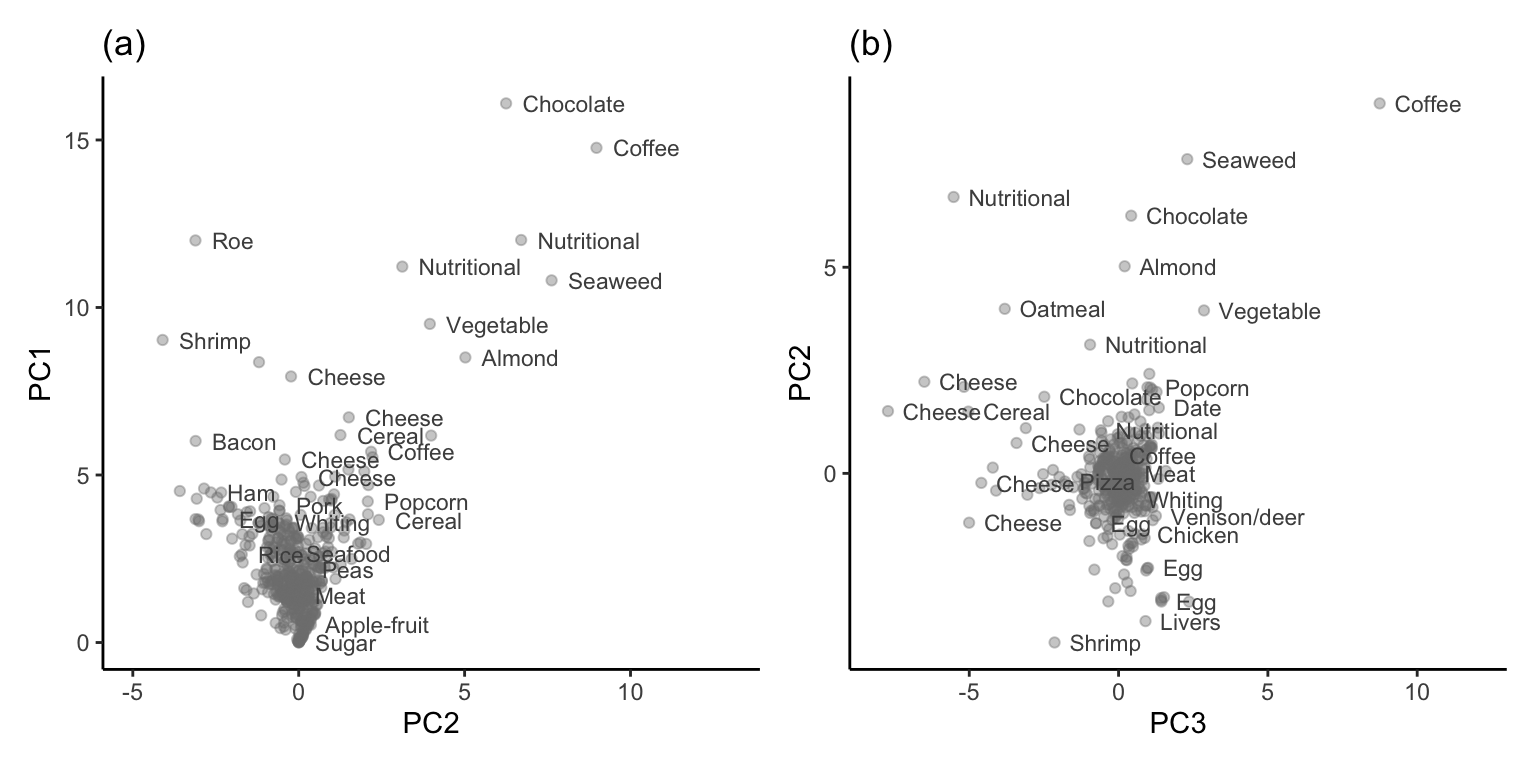
6.4.1 The Proportion of Variability Explained
Recall that the SVD of our data, \(X = U D V^T\), involves three matrices. So far, we have mainly focused our attention on the right-singular matrix, \(V\). Let’s shift our attention now to the middle matrix, \(D\). \(D\) is a diagonal matrix (meaning that all its entries are 0 except for those along the diagonal). The nonzero diagonal entries of \(D\) are called the singular values. The magnitude of the singular values indicates how strong the corresponding principal component direction is (i.e., the amount that the data “stretches” in each principal component direction). This corresponds to the amount of the variability in the original data that is being captured by each principal component.
For the six-dimensional “Major mineral” dataset (based on all FNDDS food items), \(D\) is the following \(6 \times 6\) matrix:
\[ D = \left[ \begin{array}{cccccc} 252.84 & 0 & 0 & 0 & 0 & 0\\ 0 & 97.36 & 0 & 0 & 0 & 0\\ 0 & 0 & 91.13 & 0 & 0 & 0\\ 0 & 0 & 0 & 80.76 & 0 & 0\\ 0 & 0 & 0 & 0 & 62.3 & 0\\ 0 & 0 & 0 & 0 & 0 & 45.01\\ \end{array}\right]. \tag{6.4}\]
Since the first singular value in \(D\), 252.84, is much larger than the others, this implies that the first principal component direction conveys more of the variability of the original data than the other components. An important result is that the sum of the variance of the columns in the original dataset equals the sum of the squared singular values:
\[ \sum_j Var(X_j) = \sum_j d_j^2, \tag{6.5}\]
where \(Var(X_j)\) is the variance of the \(j\)th column in the original data (which is relative to the mean if the data is mean-centered; otherwise, this variance is relative to 0), and \(d_j\) is the \(j\)th diagonal entry in the singular value matrix, \(D\). This means that the total variance of all the columns of the original dataset is the same as the variance of the principal components. From this result, it can be shown that the proportion of the variability of the original data that is captured or explained by the \(j\)th principal component is given by
\[ \textrm{prop of variability explained by PC}_j = \frac{d_j^2}{\sum_i d_i^2}. \tag{6.6}\]
Based on matrix \(D\) from Equation 6.4, the first principal component explains \(252.84^2 / 94,141.08 = 67.9\) percent of the variability in the original “Major minerals” data. Table 6.5 displays the proportion of variation explained by each of the six principal components computed from the “Major mineral” FNDDS data, as well as the cumulative proportion of the variation explained by each sequential component. From this table, we need only the first three principal components to convey almost 87 percent of the variation contained in the original six-dimensional “Major mineral” FNDDS dataset.
| Principal component | Percentage of variability explained | Cumulative percentage of variability explained |
|---|---|---|
| 1 | 67.9 | 67.9 |
| 2 | 10.1 | 78.0 |
| 3 | 8.8 | 86.8 |
| 4 | 6.9 | 93.7 |
| 5 | 4.1 | 97.8 |
| 6 | 2.2 | 100.0 |
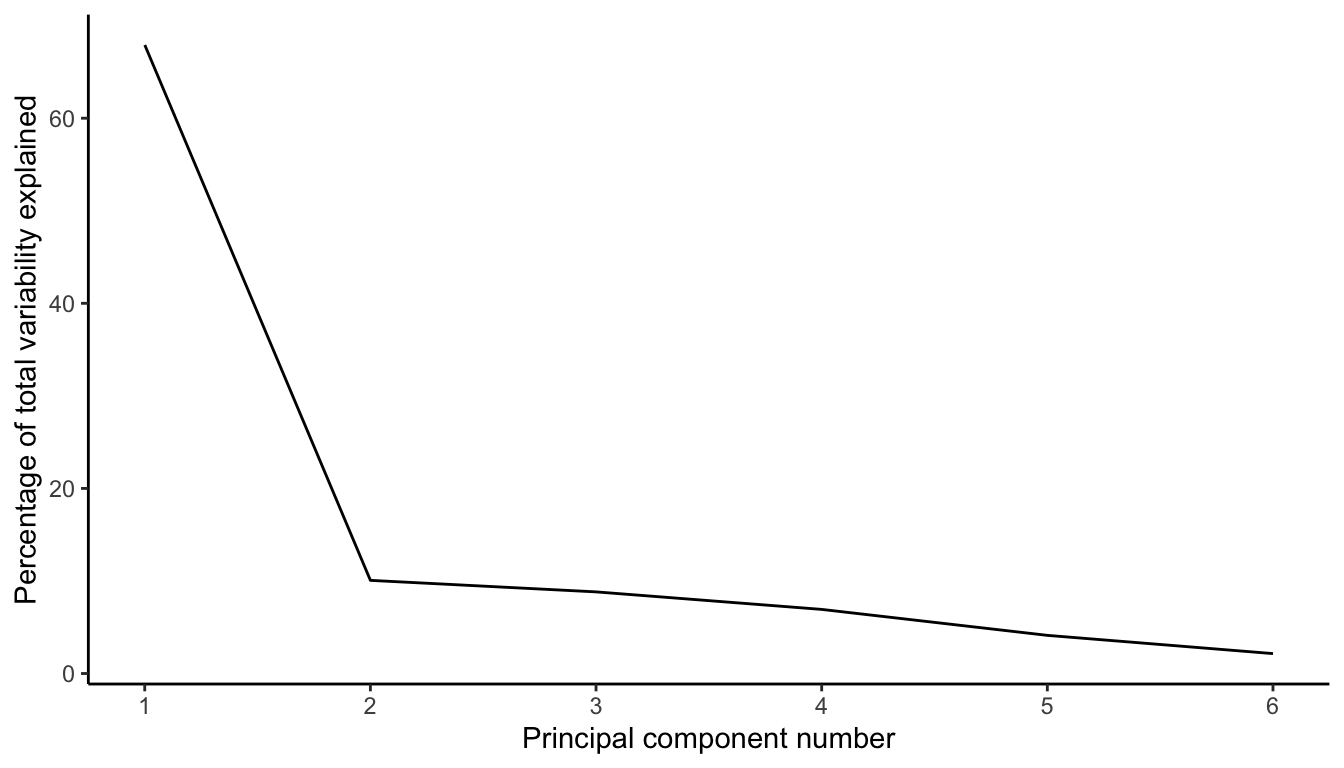
6.4.1.1 Scree Plot
A common method for assessing how many principal components to keep in the reduced dimension dataset is to create a scree plot, which shows the proportion of variability explained by each principal component either in a bar chart or as a line plot. The choice of how many components to keep is then based on when the scree curve starts to flatten out (this is sometimes called the “elbow” method).
Figure 6.8 displays a scree plot for our “Major mineral” principal components. The proportion of variability explained by each subsequent principal component drops fairly quickly and starts to flatten out (i.e., an “elbow”) at the second principal component, indicating that it might be reasonable to keep just the top 1–2 principal components. This elbow technique is a very common (and admittedly, very rough) method of choosing the number of principal components to use when summarizing a dataset.11 If you decide to use the principal components in your downstream analysis (e.g., for a predictive algorithm), then we recommend testing the stability of your downstream results to the judgment call you make about how many principal components to retain.
6.5 Preprocessing: Gaussianity and Transformations
Although we didn’t mention it above, one common assumption made when applying principal component analysis (as well as many other common analysis techniques) is that the variables all follow a theoretical multivariate Gaussian (normal) distribution. The theoretical distribution of a variable tells us what kinds of values the variable takes and how often it is likely to take each value based on strong assumptions (that are not often realistic) about how the data was generated.
A histogram showing the distribution of a variable that has a Gaussian distribution is depicted in Figure 6.9. Note the famous symmetric “bell curve” shape. The Gaussian distribution is defined using two parameters: the mean, which tells us where the “center” (peak) of the distribution lies; and the standard deviation (SD; or variance, which is the square of the SD), which tells us how far the values spread away from the center. The distribution in Figure 6.9 corresponds to the “standard” Gaussian distribution, which has mean 0 and SD 1. The smaller the SD/variance, the narrower and taller the bell curve will be. Correspondingly, the larger the standard deviation/variance, the flatter and wider the bell curve will be.
The reason we have stayed away from making distributional assumptions for our data so far is that, although many statistical techniques are based on assumptions that the variables in your data follow standard distributions (such as the Gaussian distribution), it is rare that the variables in real datasets actually follow these standard distributions. For instance, the histograms in Figure 6.10 show the distribution of the sodium, potassium, calcium, and phosphorus “Major mineral” nutrient variables from our FNDDS food dataset.
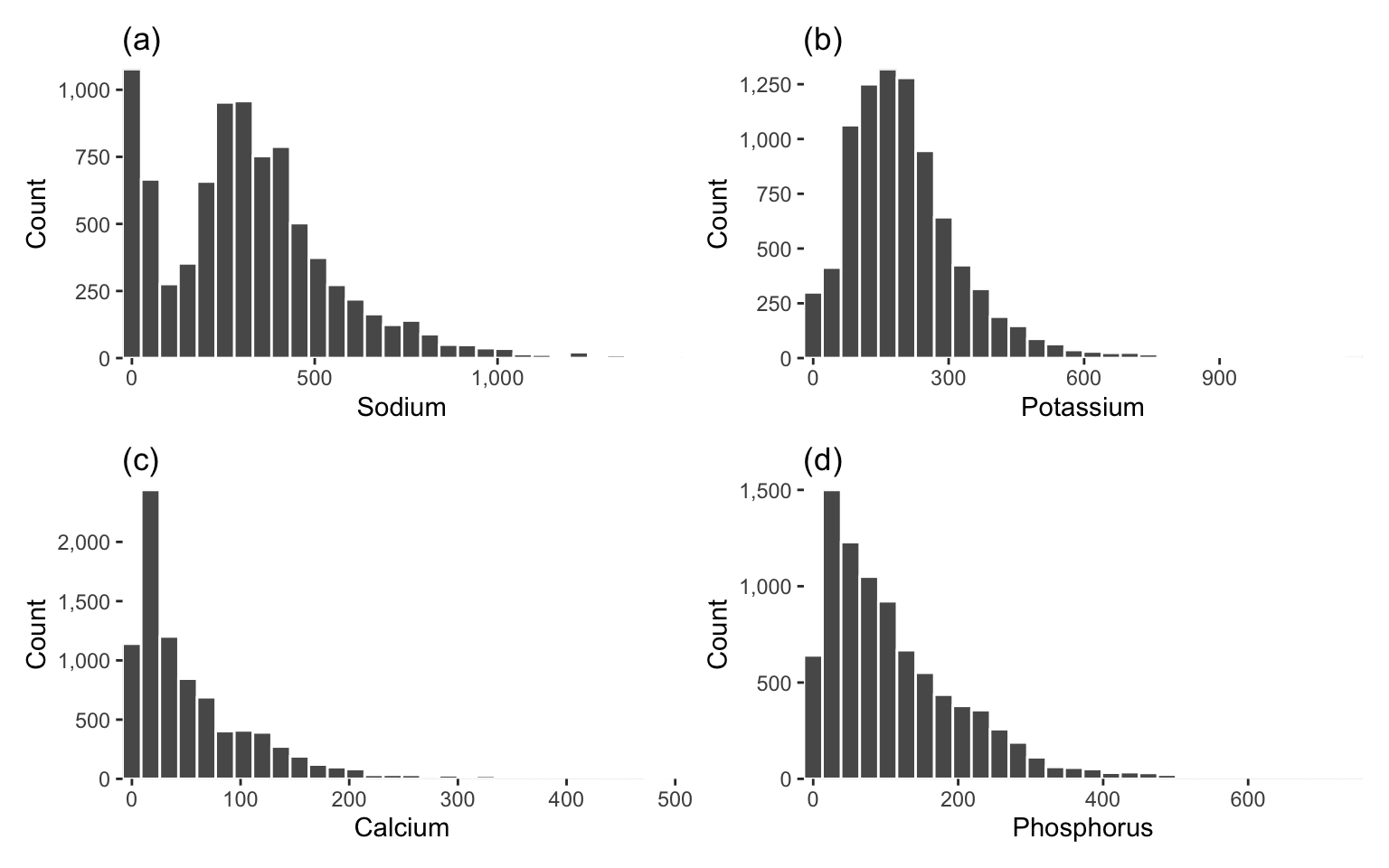
Which of these distributions look Gaussian? One of the key traits of the Gaussian distribution is symmetry around the peak, but none of these histograms look symmetric (they are all “skewed-right”—that is, they have long “tails” to the right).
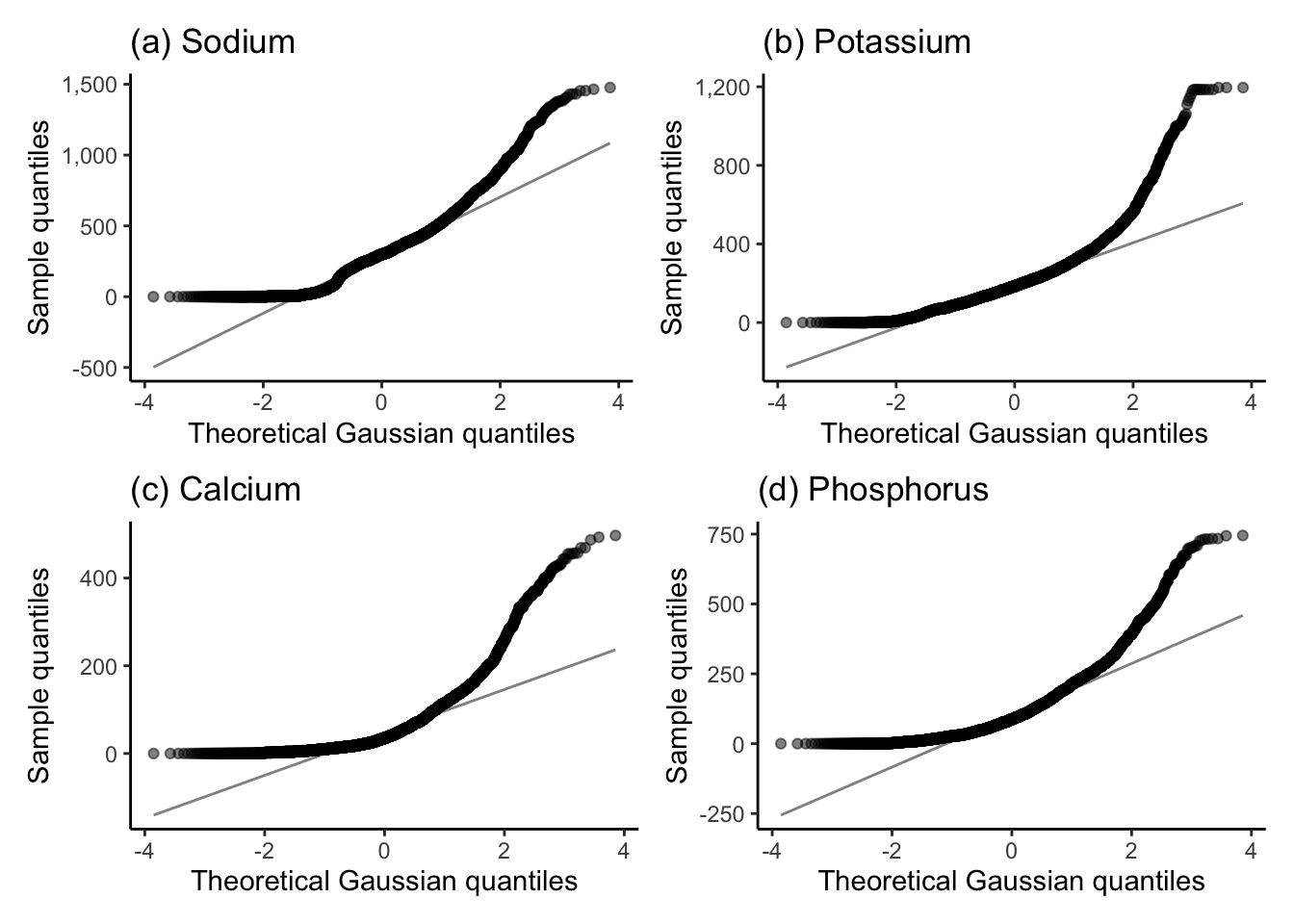
One way to check for Gaussianity more formally is to use a Q-Q plot (“quantile-quantile” plot). The Q-Q plot uses a scatterplot to compare the quantiles of your variable of interest to the quantiles of the postulated Gaussian (or other) distribution. If the distribution of your variable matches the Gaussian distribution (or other distribution of interest), then the points in the Q-Q plot will all fall along a straight diagonal line. Figure 6.11 shows the Q-Q plots for the (a) sodium, (b) potassium, (c) calcium, and (d) phosphorus “Major mineral” nutrient variables. In each of these plots, none of the points follow the straight diagonal line, indicating that each of these variables’ distributions is decidedly non-Gaussian.
While you may get more meaningful principal components (in that the components do a better job of decomposing the total variance in the data) when the variables in the data are multi-variate Gaussian, Gaussianity is not required to conduct principal component analysis.12
That said, if it is possible to transform your data to make it look more Gaussian, you will sometimes find that you end up with more meaningful principal components. A common transformation for making skewed/asymmetrical data look more Gaussian is the logarithmic transformation (variable transformation, such as a log-transformation, is a form of featurization). Recall that log-transformations tend to spread out small values that are close together and bring in large values that are far apart, reducing skewness in the data and often leading to improved symmetry. Note, however, that log-transformations require positive-valued data (or that each variable has a clear lower bound that can be added to each value to artificially make it positive).
Figure 6.12 shows the histograms, and Figure 6.13 shows the Q-Q plots, of the log-transformed “Major mineral” nutrient variables. While these log-transformations did not magically make the variables Gaussian, they did improve the symmetry of the distributions in general, and the points in the Q-Q plots are certainly following the straight line more than before the transformation.
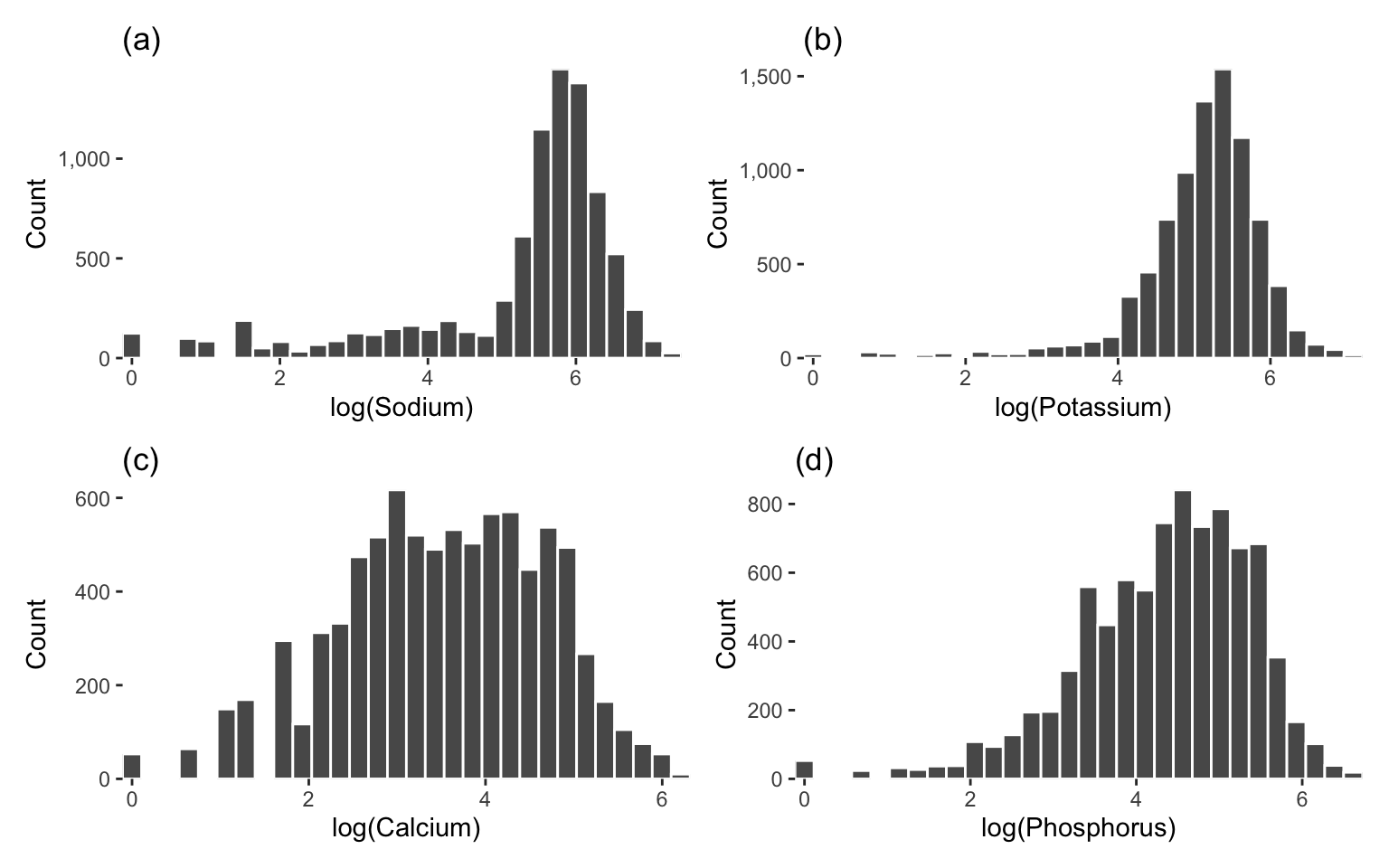
As usual, if you’re not sure whether to log-transform each variable, you can make a judgment call based on whether a log-transformation improves the symmetry of each variable, and later evaluate the impacts of this decision in a PCS stability analysis.
The first principal component linear combination13 based on the log-transformed (uncentered, SD-scaled) “Major mineral” nutrient dataset is given in Equation 6.7. Notice how similar the variable loadings are to the non-log-transformed version in Equation 6.2.
\[ \begin{align} PC1 = &~0.38~\log(\text{sodium}) +0.59~\log(\text{potassium}) \nonumber\\ &+ 0.32~\log(\text{calcium}) +0.41~\log(\text{phosphorus}) \nonumber\\ & +0.38~\log(\text{magnesium})+ 0.3~\log(\text{total choline}). \end{align} \tag{6.7}\]
Figure 6.14 shows the pairwise principal component scatterplots based on the log-transformed “Major mineral” nutrient variables. Notice how the distribution of the principal component variables are much more evenly spread throughout the space (compared with the original versions in Figure 6.7). While this is a purely subjective observation, it also seems that similar food items are more closely co-located in these log-transformed versions of the scatterplots (but this could also be because the points are more spread out, allowing us to annotate more points).
Recall from Table 6.5 that the original non-log-transformed version explained 67.9 percent of the original variability in the data. The first principal component based on the log-transformed data, however, explains 97.2 percent of the variability! This means that this single first principal component variable almost entirely captures the variation that exists in the original log-transformed dataset.
Since our project goal was to create a single variable that summarizes the “Major mineral” nutrient variables (and similarly for the other nutrient groups), this first principal component variable based on the log-transformed data is going to be a better summary than the first principal component based on the untransformed data. Based on this observation, we will make the judgment call to use the log-transformed “Major minerals” first principal component as our “Major mineral” nutrient summary variable.
6.6 Principal Component Analysis Step-by-Step Summary
To summarize the principal component analysis pipeline that we have covered in this chapter, the steps for conducting principal component analysis are shown in Box 6.5.
6.7 PCS Evaluation of Principal Component Analysis
Let’s now examine whether this “Major mineral” first principal component summary based on the log-transformed, SD-scaled, but non-mean-centered “Major mineral” dataset is predictable (i.e., that the trends it captures reemerge in a future or external setting) and stable (i.e., that the results above don’t change too much under reasonable data perturbations and alternative judgment calls).
6.7.1 Predictability
To explore the predictability of our results (based on the log-transformed, SD-scaled, and non-mean-centered version of the cleaned/preprocessed data), let’s examine whether the principal component transformations that we have computed capture similar trends when applied to the relevant portions of the external Legacy dataset that we introduced in Section 6.1. Note that the Legacy dataset has some missing values, whereas the original FNDDS dataset did not. To decide how to handle these missing values, let’s think about what we would want to happen for a user of our app. If we don’t allow them to enter foods that have missing values, we are likely to lose a lot of users, indicating that it might make sense to impute any missing values (e.g., using mean imputation).
Using the right-singular matrix, \(V\), that we computed from the original (log-transformed, SD-scaled, and non-mean-centered) FNDDS “Major minerals” data, we can compute some principal component variables for the Legacy “Major minerals” dataset using Equation 6.3, where \(X\) now represents the (log-transformed, SD-scaled, and non-mean-centered) Legacy “Major minerals” dataset (rather than the FNDDS “Major minerals” dataset).
Figure 6.15 re-creates the first versus second principal component pairwise scatterplot for 500 randomly selected Legacy dataset foods. Note that although we are only interested in the first principal component for this project, spreading out the food items using the second principal component helps to visualize the food items more clearly.
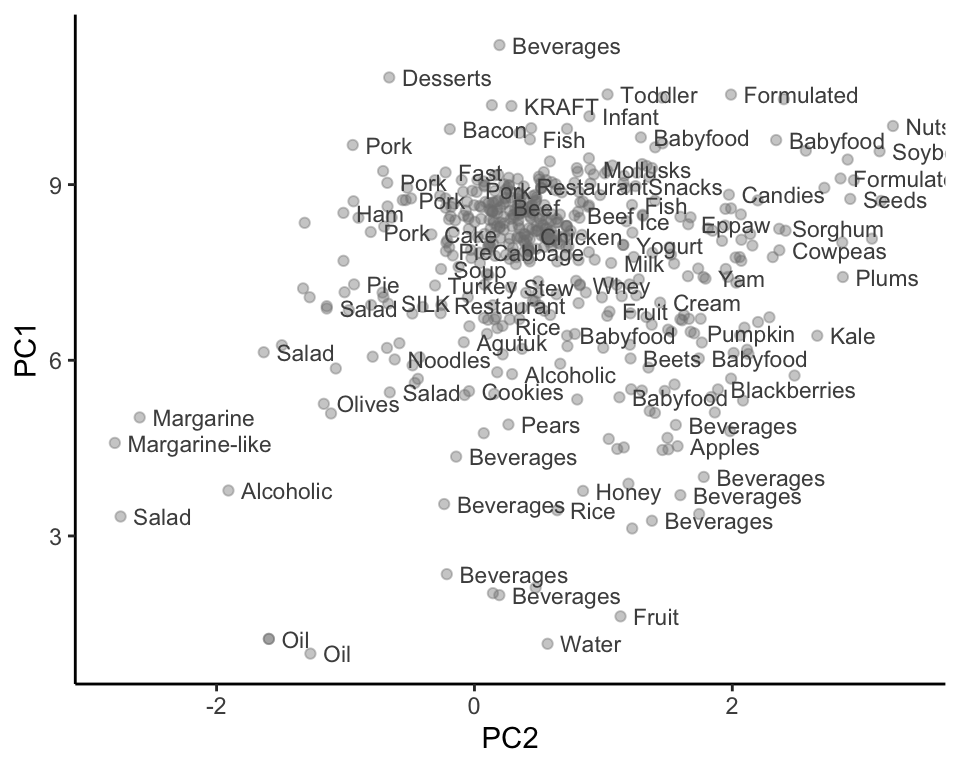
Do you think that the patterns for the Legacy food items in Figure 6.15 are similar to the patterns for the FNDDS food items in Figure 6.14(a)? To our eyes, they seem very similar, with fats and oils towards the bottom-left of the cloud of points, and meats towards the most dense center part of the cloud. At the very least, we are finding that similar Legacy food items are positioned close to one another in the PC1–PC2 space, which seems like reasonable evidence of the predictability of our principal component summary variable.
Note that this analysis is just one avenue for investigating the predictability of the specific principal component summary variables that we created using the original FNDDS data (we have just transformed the Legacy data into principal component space using the FNDDS principal components, rather than recomputing the principal components themselves using the Legacy data). If we wanted to test the predictability of the procedure that we used to generate the summary variables, we could instead recompute the summary variables themselves using the external Legacy dataset, and check that these new Legacy principal components are similar to those that were computed using the original FNDDS dataset.
6.7.2 Stability
Next, let’s investigate the stability of our principal component summary variable. Recall that the goal of stability analysis is to investigate various sources of uncertainty that arise throughout the DSLC by examining the stability of the results to reasonable changes to the data that was collected and the judgment calls made during cleaning, preprocessing, and analysis.
Keep in mind that it is unfortunately impossible to investigate all possible sources of uncertainty, so we instead recommend conducting a few select avenues of perturbation exploration, focusing on a few select types of data and judgment call perturbations. When there are multiple algorithms to choose from, we also recommend examining how your results might change across reasonable alternative algorithmic choices (although in this chapter, we consider only the principal component analysis algorithm).
6.7.2.1 Stability to Data Perturbations
To investigate the uncertainty stemming from the data collection process, we can examine the stability of our results to reasonable data perturbations. To determine what constitutes a reasonable data perturbation, we need to postulate how the data that has been observed might have looked different based on our understanding of how the data was collected. We can then use this knowledge to generate several perturbed versions of our data that are designed to represent alternative plausible versions of the data that might have arisen from the data collection process.
In this book, we typically consider two types of data perturbations that represent (1) sampling uncertainty, where we consider alternative data points that may have been included in our observed data, and (2) measurement uncertainty, where we consider alternative values that each measurement recorded in our data may have taken. Note that the decision about whether these sources of uncertainty are likely to be meaningful for a particular dataset should be justified using domain knowledge and knowledge of the data collection process.
To determine whether there is sampling uncertainty associated with our nutrition data, we need to determine whether alternative foods might have been included in the dataset. If so, random sampling perturbations can help us investigate this sampling uncertainty. Since the list of food items is not exhaustive (the dataset does not contain all possible food items), it is plausible that slightly different food items could have been included in the dataset. Moreover, as far as we can tell, the foods in the data are more-or-less “exchangeable” (one food item being included in the data has no bearing on whether another food item will be included in the data). It thus seems reasonable to investigate the stability of our results under random sampling data perturbations (we will use the bootstrap technique, which involves taking random samples with replacement—see Section 6.7.2.2).
Next, to determine whether there is measurement uncertainty associated with our nutrition data, we need to determine whether the actual nutrient measurements themselves could have been recorded differently (which could happen, for instance, if the nutrient measurement techniques are imprecise). If so, then adding appropriate amounts of random noise to some of the measurements can help us investigate this measurement uncertainty.
Unfortunately, we don’t know a huge amount about the FNDDS data collection process. This data is publicly available, and the information provided with it is limited in detail, which means that we don’t know specifically how the foods contained in the data were chosen, nor do we know specifically how the nutrient measurements were taken. However, recall from Section 6.1.1 that the FDA has a 20 percent allowable margin of error for nutrition information, and it is well known that different brands of the same food items have slightly different nutritional contents. It is thus plausible that the specific nutrition measurements recorded in the data could have been slightly different as a result of imprecise measurement techniques, alternative brands of the food items being included in the data, or even different servings of each food item being measured (perhaps one can of minestrone soup has more carrots in it than another).
These domain-based observations feel like reasonable justification for conducting a data perturbation that involves adding a small amount of random “noise” to each measurement. Specifically, to each measurement, we will add a random number drawn from a Gaussian distribution with a mean of 0 and SD of 0.2 multiplied by the mean of the corresponding variable (recall that the nutrient variables have not been mean-centered). Note that the format of the noise we have chosen to add here is itself a judgment call.
To investigate the stability of our “Major mineral” principal component summary variable to these data perturbations, we recompute the first principal component for each of four perturbed versions of the FNDDS data, where the perturbations we conduct incorporate both sampling uncertainty (via bootstrapping—see Section 6.7.2.2) and measurement uncertainty (by adding random “noise” to each measurement).
Figure 6.16 displays the (absolute value) “Major mineral” variable loadings on the first principal component based on each of the four data-perturbed versions of the FNDDS data. Notice that the loadings are extremely similar to one another, indicating that our results are very stable to these data perturbations.
Relevant code for this analysis can be found in the 03_pca.qmd (or .ipynb) file in the nutrition/dslc_documentation/ subfolder of the supplementary GitHub repository.
6.7.2.2 The Bootstrap Data Perturbation Technique
In the previous section, we used the foundational bootstrap technique to create random perturbed samples from our data. Bootstrapping (Figure 6.17(a)) involves taking random samples of your data “with replacement,” which means that if the sample is created by repeatedly drawing observations at random to be included in the sample, once an observation has been chosen for inclusion in the sample, it is immediately “replaced” in the pool of observations so it can potentially be chosen again. Each observation therefore has the potential to be included in the bootstrap sample multiple times (although, by random chance, it may not be included at all).14
Why do we use the bootstrap, rather than the (possibly more intuitive) subsampling technique, which involves taking a random subset of your data “without replacement” so that no observation can be chosen more than once? Bootstrapping and subsampling are each depicted in Figure 6.17. The main difference between the two perturbation techniques is that a subsample will always contain fewer observations than the original dataset. If a subsample had the same number of observations as the original dataset, then it would be exactly identical to it, since every observation will be included exactly once. However, because each observation can be included multiple times (or not at all) in a bootstrapped sample, bootstrapping allows you to compute perturbed versions of the dataset that have the same number of observations as the original dataset, while also containing a different set of observations to the original dataset. For this reason, bootstrapping is typically preferred over subsampling in traditional statistical inference, such as when computing empirical estimates of an SD, since such computations typically depend on the sample size.
6.7.2.3 Stability to Cleaning and Preprocessing Judgment Calls
While we are fairly confident in our decisions to not mean-center our data and to apply a log-transformation to each of our “Major mineral” nutrient variables (based on domain knowledge and our earlier explorations), let’s take a moment to investigate the stability of our principal components to these preprocessing choices. Figure 6.18 shows the variable loading on each “Major mineral” nutrient for the first principal component based on whether we conduct a log-transformation (represented by each panel) and whether we mean-center the data (represented by the color of the bars). Note that since the log-transformation changes the magnitude of the variable loadings, we don’t want to directly compare the loadings for the log-transformed variables with the non-log-transformed variables, which is why we present them in separate panels in Figure 6.18 (the rankings of the loadings are still comparable, though).
Notice that the loadings are notably less stable to these preprocessing judgment call perturbations than they were to the data perturbations (shown in Figure 6.16). This indicates that these judgment calls do in fact have a notable effect on the principal components. Since we feel that the results based on the log-transformed results were more meaningful overall (see Section 6.5), and domain knowledge indicates that we need not mean-center our results, we will continue to primarily consider the log-transformed and non-mean-centered version of our principal components.
6.8 Applying Principal Component Analysis to Each Nutrient Group
So far in this chapter, we have focused only on creating a summary variable (using the first principal component) for the “Major minerals” nutrients. However, we can use the same approach to create summary variables for each of the other nutrient groups. Figure 6.19 presents bar charts depicting the PC1 loadings for each of the “Fat,” “Vitamin,” “Major mineral,” and “Trace mineral” nutrient groups.
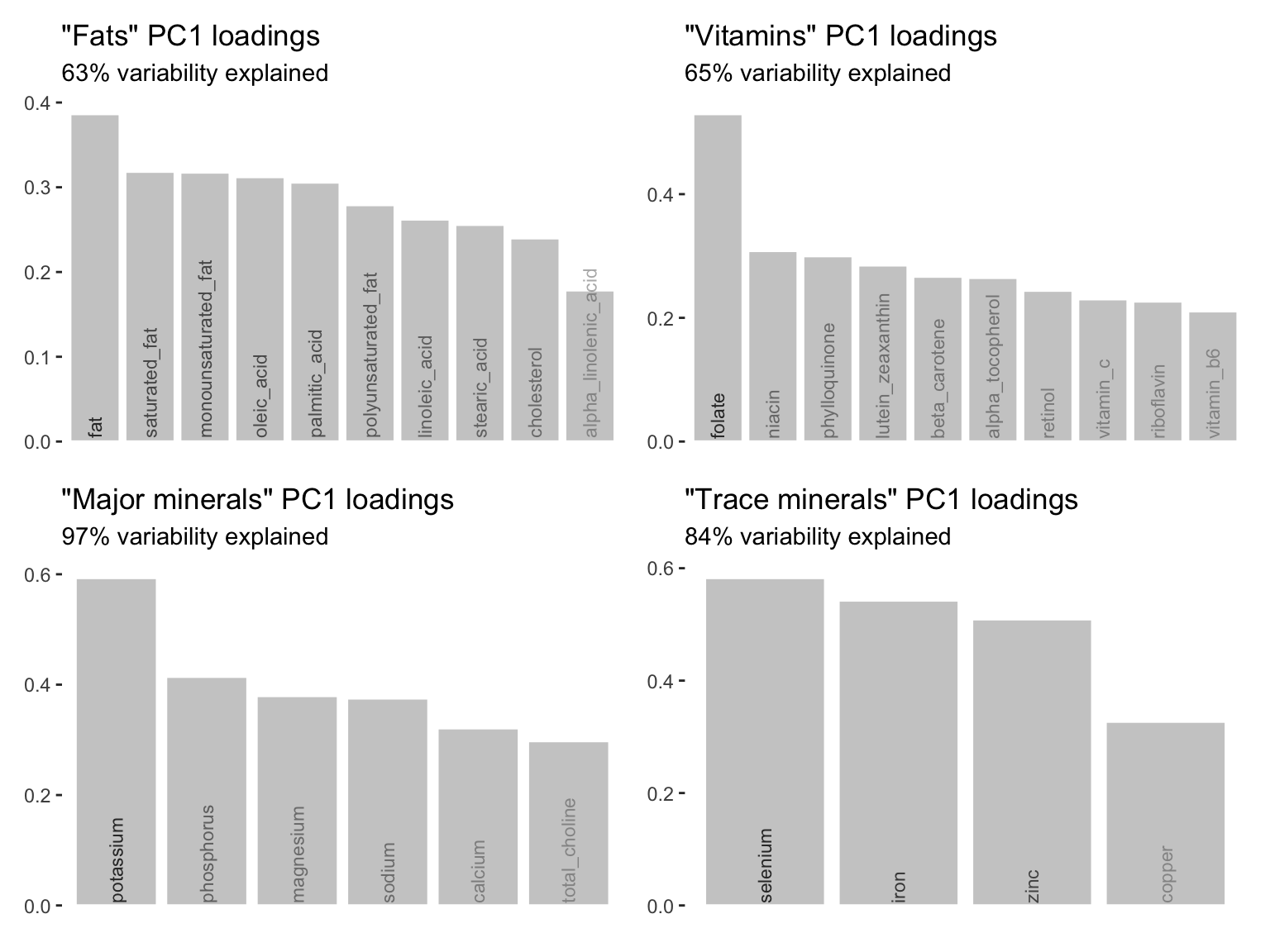
All nutrient group datasets have been SD-scaled, have not been mean-centered, and all the variables have been log-transformed. Note from Figure 6.19 that the first principal components for the other nutrient groups do not explain quite as much of the variation in the respective datasets as the “Major mineral” first principal component did, but they are still capturing the majority of the variation in the original datasets.
Table 6.6 shows the food items from Table 6.1 in terms of each of the principal component-based nutrient group summary variables. To help with the interpretation of these principal component-based nutrient summary variables, we could apply some thresholding rules (e.g., based on the quartiles) to determine whether each food item is “very low,” “low,” “high,” or “very high” for each nutrient group summary variable.
| Food | Fats | Vitamins | Major Minerals | Trace Minerals | Carbs | Calories | Protein |
|---|---|---|---|---|---|---|---|
| Ice cream sandwich | 5.1 | 2.1 | 9.2 | 2.3 | 3.4 | 5.9 | 2.1 |
| Cheese sandwich | 10.1 | 4.8 | 10.1 | 3.5 | 3.1 | 6.4 | 2.9 |
| Herring | 10.6 | 6.0 | 11.7 | 3.6 | 0.0 | 5.8 | 3.6 |
| Hamburger | 6.5 | 4.2 | 10.1 | 4.0 | 2.9 | 6.0 | 3.1 |
| Turkey with gravy | 2.8 | 4.3 | 9.4 | 1.9 | 2.8 | 5.3 | 2.3 |
| Oxtail soup | 3.9 | 2.9 | 8.3 | 3.1 | 0.8 | 4.8 | 2.5 |
| Bread | 2.3 | 4.5 | 10.2 | 4.1 | 4.7 | 6.1 | 2.6 |
| Pancakes | 5.7 | 4.5 | 10.8 | 2.6 | 3.6 | 6.0 | 2.4 |
| Pizza | 5.8 | 5.3 | 10.2 | 3.4 | 3.5 | 6.0 | 2.7 |
| Rice | 2.0 | 2.7 | 8.4 | 1.6 | 3.0 | 5.1 | 1.3 |
| Tomato | 0.2 | 2.6 | 7.8 | 0.9 | 2.3 | 3.9 | 0.8 |
| Tomato with corn and okra | 2.6 | 3.9 | 8.6 | 0.9 | 2.5 | 4.2 | 1.0 |
| Tomato rice soup | 1.0 | 2.1 | 7.0 | 0.9 | 2.1 | 4.2 | 0.7 |
| Vegetable combination | 1.6 | 4.1 | 8.9 | 1.3 | 3.1 | 4.6 | 1.4 |
| Spinach | 1.6 | 3.7 | 9.2 | 1.4 | 2.3 | 3.9 | 1.4 |
Table 6.7 shows one possible set of thresholded values for the data from Table 6.6, which could be used as an interpretable summary of each food item in our app.
| Food | Fats | Vitamins | Major Minerals | Trace Minerals | Carbs | Calories | Protein |
|---|---|---|---|---|---|---|---|
| Ice cream sandwich | high | very low | low | high | very high | high | high |
| Cheese sandwich | very high | very high | high | very high | high | very high | very high |
| Herring | very high | very high | very high | very high | very low | high | very high |
| Hamburger | very high | high | high | very high | high | very high | very high |
| Turkey with gravy | low | high | high | low | high | low | high |
| Oxtail soup | high | low | low | high | very low | low | high |
| Bread | low | very high | high | very high | very high | very high | high |
| Pancakes | high | very high | very high | high | very high | very high | high |
| Pizza | high | very high | high | very high | very high | high | high |
| Rice | low | low | low | low | high | low | low |
| Tomato | very low | very low | very low | very low | low | very low | very low |
| Tomato with corn and okra | low | high | low | very low | low | very low | very low |
| Tomato rice soup | very low | very low | very low | very low | low | very low | very low |
| Vegetable combination | very low | high | low | low | high | low | low |
| Spinach | very low | high | low | low | low | very low | low |
A more detailed summary of this analysis can be found in the 03_pca.qmd (or .ipynb) file in the nutrients/dslc_documentation/ subfolder of the supplementary GitHub repository.
6.9 Alternatives to Principal Component Analysis
Principal component analysis is characterized by defining a set of new orthogonal variables corresponding to linear combinations of the original variables that capture the maximal directions of variability in the data. However, principal component analysis is just one of many possible methods for summarizing the patterns and trends in a dataset. While we don’t cover them in this book, common alternative approaches (and references) include nonnegative matrix factorization (Lee and Seung 1999), independent component analysis (Hyvärinen, Karhunen, and Oja 2001), sparse dictionary learning (sparse coding) (Olshausen and Field 1997), kernel principal component analysis (Schölkopf, Smola, and Müller 1998), UMAP (McInnes, Healy, and Melville 2020), t-SNE (Van der Maaten and Hinton 2008), and autoencoder (Goodfellow, Bengio, and Courville 2016).
Exercises
True or False Exercises
For each question, specify whether the answer is true or false (briefly justify your answers).
The technique of SVD is used only for principal component analysis.
Any matrix can be decomposed using SVD.
The principal component variable loading magnitudes are comparable only if the variables are mean-centered.
If principal component analysis is applied to data with positive values, the variable loadings will all be positive too.
We are only ever interested in the first principal component.
Data cleaning/preprocessing judgment calls can affect the results of principal component analysis.
Principal component analysis can be applied only to datasets with numeric variables.
Principal component analysis only creates summary variables consisting of linear combinations of the original variables.
The projected data points will exhibit greater variability when projected onto the second principal component than the first principal component.
The principal component analysis algorithm requires that the columns in your data have a Gaussian distribution.
A scree plot displays the proportion of variability explained by each principal component.
Conceptual Exercises
Describe, in your own words, what the first principal component is capturing.
What information do the matrices \(V\) and \(D\) contain in the SVD decomposition of a matrix, \(X = U D V^T\)?
Suppose that after performing SVD on a four-dimensional dataset, you obtained a right-singular vector matrix, \(V\), whose first column is: \[\left[\begin{array}{c} 0.010\\ 0.003\\ 0.047\\ 0.999 \end{array}\right].\] If the original data had variables \(x_1, x_2, x_3, x_4\), write the formula for computing the first principal component.
Explain why we often want to SD-scale the variables (divide each column by its SD) before applying principal component analysis. When might we not want to do this?
For each of the following projects listed here, discuss whether you think it makes sense to mean-center and SD-scale each of the variables. Describe how you would use principal components analysis to achieve the project goal.
Your goal is to obtain a single number that you can use to summarize the progression of a patient’s ovarian cancer which is usually determined based on dozens of various measurements from blood tests (including the number of white blood cells, the number of red blood cells, and so on). Each variable in your data is the measurement from a blood test, which corresponds to a count whose minimum value is 0. Each count has a different scale (e.g., we typically have trillions of red blood cells per liter, but only billions of white blood cells).
Your goal is to develop an algorithm that will predict how much houses will sell for in your city. Your data consists of a large number of numeric features (e.g., the area, quality, and number of bedrooms) for several thousand houses that have recently been sold, and you aim to create a simpler lower-dimensional dataset that you can use as the input for your predictive algorithm.
You are hoping to learn about public opinion on autonomous vehicles. Your goal is to create a simple visualization, such as a scatterplot or a histogram, that can be used to visualize the different categories of people based on their answers to a survey. The survey is conducted on random members of the public and asks dozens of questions whose answers are each on a scale of 0 to 5, such as “How safe do you think autonomous vehicles are?” and “How much do you know about autonomous vehicle technology?”
Mathematical Exercises
If \(A = \left( \begin{smallmatrix} 2.1 & 3.5\\ -1.2 & 7.9 \end{smallmatrix} \right)\), and \(B = \left( \begin{smallmatrix} 1.6 & -5.4\\ 5.3 & 2.0 \end{smallmatrix} \right),\) compute the product, \(AB\), manually (by hand) and verify your computation, e.g., using R or Python.
If \(A= \left( \begin{smallmatrix} 2.1 & 3.5\\ -1.2 & 7.9 \end{smallmatrix} \right)\) is a \(2 \times 2\) matrix, and \(Y=\left( \begin{smallmatrix} 4 \\ 9 \end{smallmatrix} \right)\) is a \(2 \times 1\) column vector, compute the product, \(AY\), manually (by hand) and verify your computation, e.g., using R or Python.
Suppose that after conducting principal component analysis, you obtained a singular value matrix, \(D\), which is given by \[D = \left[\begin{array}{cccc} 30.6 & 0 & 0 &0 \\ 0 & 16.2 & 0 & 0\\ 0 & 0 & 11.2 & 0\\ 0 & 0 & 0 & 6.08\\ \end{array}\right],\] and a right-singular vector matrix, \(V\), which is given by \[V = \left[\begin{array}{cccc} 0.45 & -0.60 & -0.64 & 0.15 \\ -0.40 & -0.80 & 0.42 & -0.17 \\ 0.57 & -0.01 & 0.23 & -0.78\\ 0.54 & -0.08 & 0.59 & 0.58\\ \end{array}\right].\] Based on these matrices, answer the following questions:
Is it possible to determine how many variables (columns) the original data contained? If so, how many?
Is it possible to determine how many observations (rows) the original data contained? If so, how many?
Is it possible to determine how many principal components were computed? If so, how many?
Compute the proportion of variability explained for each principal component.
Write a formula (linear combination) for computing each of the first two principal components (using \(x_1, x_2,\) etc… to represent the original variables).
Compute the first two principal component values for an observation whose measurements are \((0.65, ~-1.09, ~1.21, ~0.93)\).
Coding Exercises
The code for cleaning and exploring the nutrition data from this chapter can be found in the
01_cleaning.qmdand02_eda.qmd(or.ipynb) files in thenutrition/dslc_documentation/subfolder of the supplementary GitHub repository. Run the code and read through the discussion in each of these files and add any other explorations that you wish to conduct. For an advanced version of this exercise, conduct your own cleaning and exploratory analyses of this data.The code for conducting principal component analysis from this chapter on the nutrition dataset can be found in the
03_pca.qmd(or.ipynb) file in thenutrition/dslc_documentation/subfolder of the supplementary GitHub repository.- For the “Major minerals” dataset, compute the correlation between each original “major mineral” nutrient variable and the principal components you computed. Compare these correlations with the variable loadings. The section in the
03_pca.qmd(or.ipynb) file in thenutrition/dslc_documentation/subfolder is labeled “[Exercise: to complete]”.
- For the “Major minerals” dataset, compute the correlation between each original “major mineral” nutrient variable and the principal components you computed. Compare these correlations with the variable loadings. The section in the
Create a scree plot (using ggplot2 in R or your preferred visualization library in Python) based on the following singular value matrix \[D = \left[\begin{array}{cccc} 357.2 & 0 & 0 &0 \\ 0 & 26.2 & 0 & 0\\ 0 & 0 & 12.3 & 0\\ 0 & 0 & 0 & 9.1\\ \end{array}\right].\] How many principal components would you choose to keep, based on the elbow method?
Project Exercises
Palmer Penguins The Palmer Penguins dataset contains measurements on size and weight, as well as other characteristics for almost 350 penguins, where each penguin is one of three species (Adelie, Chinstrap, or Gentoo). This data can be loaded into R by installing and loading the
palmerpenguinsR package (Horst, Hill, and Gorman 2020), and the data has also been provided in theexercises/penguins/data/folder in the supplementary GitHub repository. There are two alternative versions of the data that you may choose to use for this project:penguins_raw, a version of the data that you will have to clean yourself, andpenguins, which is a simplified version of thepenguins_rawdata that has already been “cleaned” for you (although you are welcome to perform any additional cleaning of this data).The goal of this project is to come up with a simple principal component-based predictive algorithm for predicting the species of any penguin that you meet in the wild (including on a different island than the islands from which the data was originally collected).
Take 30 percent of the penguins and place them in a validation set. Think about how you want to split up the data in terms of how you will be applying your algorithm. Justify your choice, and summarize it in your DSLC documentation.
Clean your dataset of choice by creating and completing a
01_clean.qmd(or.ipynb) file, which you may want to place in adslc_documentation/subfolder. Be sure to thoroughly document the process (including any judgment calls that you made).Conduct an exploratory data analysis of the training data by creating and completing a
02_eda.qmd(or.ipynb) file in thedslc_documentation/subfolder. Be sure to create at least one explanatory figure.Conduct a principal component analysis of the entire training dataset in a file called
03_pca.qmd(or.ipynb) in thedslc_documentation/subfolder, which you will need to create. Be sure to write down the formula for computing the first principal component in terms of a penguin’s original measurements.Visualize the distribution of the values for the first principal component and try to differentiate the values from each penguin species (e.g., using color).
Come up with some simple thresholding rules for classifying penguins into one of the three species using the first principal component. For example, such a set of rules might be “If PC1 \(> 0\), then classify as Adelie; if \(-1 <\) PC1 \(< 0\), then classify as Chinstrap; if PC1 \(< -1\), then classify as Gentoo” (these are just example threshold values—yours will almost certainly be different!)
Conduct a predictability analysis by estimating the accuracy of your PC1-based thresholding rule based on how many of the withheld validation set penguins’ species are correctly classified using your thresholding rule.
Conduct a stability analysis by investigating how your results change when you conduct various perturbations throughout the DSLC (including reasonable data perturbations, reasonable data cleaning and preprocessing judgment call perturbations, and reasonable perturbations to any analysis judgment calls that you made).
References
Fukagawa, Naomi K, Kyle McKillop, Pamela R Pehrsson, Alanna Moshfegh, James Harnly, and John Finley. 2022. “USDA’s FoodData Central: What Is It and Why Is It Needed Today?” American Journal of Clinical Nutrition 115 (3): 619–24.
Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. MIT Press.
Horst, Allison Marie, Alison Presmanes Hill, and Kristen B Gorman. 2020. “Palmerpenguins: Palmer Archipelago (Antarctica) Penguin Data.”
Hotelling, H. 1933. “Analysis of a Complex of Statistical Variables into Principal Components.” Journal of Educational Psychology 24 (6): 417–41.
Hyvärinen, Aapo, Juha Karhunen, and Erkki Oja. 2001. Independent Component Analysis. 1st ed. Wiley-Interscience.
Jumpertz, Reiner, Colleen A Venti, Duc Son Le, Jennifer Michaels, Shannon Parrington, Jonathan Krakoff, and Susanne Votruba. 2013. “Food Label Accuracy of Common Snack Foods.” Obesity 21 (1): 164–69.
Lee, Daniel D., and H. Sebastian Seung. 1999. “Learning the Parts of Objects by Non-Negative Matrix Factorization.” Nature 401 (6755): 788–91.
McInnes, Leland, John Healy, and James Melville. 2020. “UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction.” arXiv, September.
Noh, Mohd Fairulnizal Md, Rathi Devi-Nair Gunasegavan, Norhayati Mustafa Khalid, Vimala Balasubramaniam, Suraiami Mustar, and Aswir Abd Rashed. 2020. “Recent Techniques in Nutrient Analysis for Food Composition Database.” Molecules 25 (19): E4567.
Olshausen, Bruno A., and David J. Field. 1997. “Sparse Coding with an Overcomplete Basis Set: A Strategy Employed by V1?” Vision Research 37 (23): 3311–25.
Pearson, Karl. 1901. “LIII. On Lines and Planes of Closest Fit to Systems of Points in Space.” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, November.
Schölkopf, Bernhard, Alexander Smola, and Klaus-Robert Müller. 1998. “Nonlinear Component Analysis as a Kernel Eigenvalue Problem.” Neural Computation 10 (5): 1299–319.
Stewart, G. W. 1993. “On the Early History of the Singular Value Decomposition.” SIAM Review 35 (4): 551–66.
Van der Maaten, Laurens, and Geoffrey Hinton. 2008. “Visualizing Data Using t-SNE.” Journal of Machine Learning Research 9 (11): 2579–2605.
Principal component analysis is often referred to using the acronym PCA, which has nothing to do with the veridical data science acronym PCS. It is common to use the acronym PC for “principal component,” but to reduce confusion with PCS, we will refrain from using the PCA acronym.↩︎
The nutrition databases and associated information from the UDSA website can be found at https://fdc.nal.usda.gov/.↩︎
The data also contained a few additional variables (e.g., moisture, alcohol, caffeine, and theobromine) that we decided did not fit with the remaining variables, so we removed these from the data when we cleaned/preprocessed it.↩︎
Note that this is just one possible way to define what we mean by the “best” linear combination—can you think of any others?↩︎
If your data has been mean-centered (i.e., the mean of each column has been subtracted from each value in the column to create a collection of transformed columns whose means all equal zero), the origin will correspond to the average data point (i.e., the data point whose measurements for each variable corresponds to the average/mean value across all the observations). If, however, your data has not been mean-centered, then the origin corresponds to the “zero” data point, whose measurements across all variables all equal 0.↩︎
The variation is relative to the mean of the data if the data has been mean-centered, and it is relative to the zero data point if it has not.↩︎
SVD has been used in mathematics since the 1800s (Stewart 1993).↩︎
This is because the process of computing the covariance matrix essentially involves mean-centering the data.↩︎
Multiplying a matrix by another matrix corresponds to rotating and/or stretching the original dimensions of the data space of the first matrix based on various properties of the second matrix.↩︎
Technically, we are presenting the negative of \(V\), which is equivalent to \(V\). For demonstration purposes, it is helpful to have positive variable loadings in PC1.↩︎
Another technique for choosing the number of components involves cross-validation (CV), which we will introduce in the context of clustering in Chapter 7.↩︎
However, many of the theoretical results concerning the results of principal component analysis require that the original variables each have a (multi-variate) Gaussian distribution.↩︎
Again, we are presenting the negative of the first principal component for demonstration purposes.↩︎
Note that for a bootstrap sample to be a plausible representation of an alternative version of the data, the original data points should be exchangeable and not have underlying groupings.↩︎