13  Producing the Final Prediction Results

This is a pre-release of the Open Access web version of Veridical Data Science. A print version of this book will be published by MIT Press in late 2024. This work and associated materials are subject to a Creative Commons CC-BY-NC-ND license.

The traditional approach to machine learning (ML) involves training a predictive algorithm on just one version of the cleaned/preprocessed training dataset and using the best-performing algorithm (evaluated using the corresponding validation set) to generate the final predictions for future data points. However, while this approach considers alternative algorithms, it does not consider alternative versions of the data used to train the algorithms. Specifically, the traditional ML approach ignores the uncertainty that arises from the specific dataset that was used to train the algorithm, including the judgment calls that we made during cleaning and preprocessing. In contrast, in the predictability, computability, and stability (PCS) framework, we train a variety of plausible alternative predictive fits, where each predictive fit corresponds to one particular algorithm trained using one particular version of the cleaned/preprocessed training data.

Box 13.1: PCS Predictive Fit

In the PCS framework, a predictive fit (or just a “fit”) refers to the pairing of an algorithm and a particular cleaned/preprocessed training dataset used for training the algorithm.

Note, however, that an algorithm trained on a dataset that has a particular format can only generate predictions for new data points whose format matches that of the data it was trained on. For this reason, to generate a prediction for future data points using a given predictive fit, the future data points need to be cleaned/preprocessed in the same way as the training dataset that was used to define the fit.

By considering a range of predictive fits that correspond to a variety of combinations of algorithms and alternative cleaned/preprocessed training datasets, we can examine the uncertainty that arises not only from our choice of algorithm but also from the cleaning/preprocessing judgment calls that underlie our predictions.

As a reminder, each alternative cleaned/preprocessed version of the training data is based on the same set of original training data observations. The differences between them come from the distinct set of cleaning/preprocessing action items that were applied to the original training dataset. However, note that if some of your cleaning/preprocessing judgment call options involve removing data points (e.g., removing entire observations that contain missing values), then your performance evaluations must be based only on the set of observations that are common across all the cleaned/preprocessed datasets. This is because performance evaluations based on differing sets of data points are not comparable. Keep in mind that it is recommended that you retain as many of the observations as possible during cleaning and preprocessing (recall that we advise against removing observations in general), so ideally each of the cleaned/preprocessed versions of the validation data will contain very similar sets of observations.

Regardless of what data you are applying your fits to, the PCS predictive fit framework involves computing a prediction for each combination of cleaning/preprocessing protocols and algorithms. This means that many alternative predictions are produced for each data point, which provides a sense of the uncertainty that underlies each prediction. However, presenting tens, hundreds, or even thousands of potential predictions for each data point to our real-world users is not practical.

To solve this problem, we need to decide how to combine the range of potential predictions in a way that is accurate and still manages to convey (or at least takes into account) the range of predictions that could be computed for each observation. In this chapter, we will introduce three possible approaches for combining the predictions from a collection of PCS predictive fits:

• The single PCS predictive fit. As the veridical data science analog of the traditional approach, this approach involves identifying the single PCS predictive fit with the highest validation set predictive performance. Future predictions for new data points are then computed using the chosen predictive fit. If the best-performing fit does not pass a problem-specific predictability screening on the validation set (i.e., if the best-performing algorithm does not achieve adequate performance as dictated by the domain problem), then no predictive fit should be used. By considering the PCS predictive fits that span a range of alternative algorithmic and cleaning/preprocessing options, this approach takes into account the uncertainty arising from the algorithm and cleaning/preprocessing choices when computing the prediction. However, by presenting just a single prediction value as the final output, this uncertainty is not conveyed to the user.

• The PCS ensemble. Instead of choosing just one PCS predictive fit, this approach creates an ensemble from the PCS predictive fits that pass a problem-specific predictability screening on the validation set. One way to compute the ensemble’s response prediction for a future data point is by computing the average response prediction for continuous responses or a majority vote for binary responses. By considering a range of alternative algorithmic and cleaning/preprocessing judgment call options, this approach takes into account the uncertainty arising from the algorithmic and cleaning/preprocessing judgment calls when computing the prediction. However, by presenting a single prediction value as the output, this approach also does not convey this uncertainty to the user.

• The PCS calibrated PPIs. Rather than providing a single prediction for each new data point (e.g., using a single fit or an ensemble), this approach creates an interval using the predictions from the fits that pass a problem-specific predictability screening on the validation set. These intervals are called prediction perturbation intervals (PPIs). Because the length of the interval will typically depend on the number of predictions used to create it, the intervals are calibrated to achieve a prespecified coverage level (e.g., the lengths of the intervals are modified to ensure that 90 percent of the validation set intervals contain the observed response). Currently, this interval-based approach is only designed for continuous response predictions.¹ By presenting an interval based on the range of alternative algorithmic and cleaning/preprocessing options, this approach can convey the underlying prediction uncertainty to the user.

Each approach involves using a problem-specific predictability screening (P-screening) technique to filter out poorly performing PCS predictive fits based on the validation set performance. Unfortunately, however, once you’ve used the validation set to perform predictability screening, the validation data points can no longer be used to generate an independent assessment of your final predictive performance. Fortunately, we knew that this time would come, and we prepared for it by creating the test set. The test set, just like the validation set, was set aside at the beginning of the project and, like the validation set, was designed to be a representation of actual future or external data. (However, if you’re lucky enough to have actual future data available, then you’ll want to evaluate your final predictions using this future data instead.)

Which of these three approaches to use will depend on the specific prediction problem being solved. For instance, if the domain problem requires a single prediction output with a very clear and transparent computational pipeline, then the first approach, which is based on the single best-performing predictive fit, will probably be the most appropriate. In contrast, if it is particularly important to convey a sense of the underlying uncertainty of the predictions, then the third (interval-based) approach will be more appropriate. Note, however, that these are just three of many possible approaches that you could use to aggregate the predictions produced from an array of predictive fits. Can you come up with any others?

Section 13.1 to Section 13.3 of this chapter will expand on each of these three final prediction formats and will provide demonstrations for both the continuous response Ames house price project and the binary response online shopping project. At the end of this chapter, in Section 13.5, we will briefly discuss several considerations for making your final predictions available to your users.

13.1 Approach 1: Choosing a Single Predictive Fit Using PCS

The first approach for choosing the final prediction format is to present the single best PCS predictive fit based on the validation set performance. However, unlike the traditional ML approach that selects the best algorithm trained on just one possible version of the cleaned/preprocessed training dataset, this PCS-based approach selects the best algorithm across many possible versions of the cleaned/preprocessed training datasets. That is, the PCS approach to choosing the best fit identifies the best combination of algorithm and cleaning/preprocessing judgment calls (i.e., the best predictive fit, rather than the best predictive algorithm).

Figure 13.1(a) depicts the process of choosing the single PCS predictive fit that achieves the best validation set predictive performance across four algorithms, each trained on two different cleaned/preprocessed versions of the training data, corresponding to eight predictive fits in total. (Note, however, that in practice, you will generally have many more than two alternative cleaning/preprocessing judgment call combinations.) Having identified the best PCS predictive fit, Figure 13.1(b) depicts using this fit to compute a response prediction for a new data point.

Figure 13.1: The single best fit approach. This diagram depicts (a) the predictability screening process of identifying the single best fit based on the validation set predictive performance from among all fits based on four different continuous response algorithms (LS, LAD, RF, and ridge), each trained on two alternative versions of the cleaned and preprocessed judgment call–perturbed training dataset, and (b) generating a prediction for a new data point using the best fit.

If none of the PCS predictive fits pass a predictability screening based on a desired domain problem-specific performance threshold, then it is recommended that you do not make any of the predictive fits available for use in practice.

Choosing a single PCS predictive fit involves the following steps:

1. Predictability screening: Identify which fit has the best validation set performance.

   1. Create and document several different versions of the cleaned and preprocessed training and validation sets using different combinations of cleaning and preprocessing judgment calls.² Let \(K\) denote the number of cleaned/preprocessed datasets you end up with.

   2. Train each predictive algorithm (e.g., LS, RF, and so on) using each of the \(K\) cleaned/preprocessed training datasets. If you have \(L\) different algorithms, then you will end up with \(K \times L\) predictive fits.

   3. Generate a response prediction for each validation set observation using each of the \(K \times L\) predictive fits.³

   4. Identify which predictive fit from among the \(K \times L\) fits yields the best validation predictive performance. This is the best PCS fit.

2. Computing predictions for new observations: Predictions for new observations can be computed using the best PCS fit.

3. Test set evaluation: Evaluate your best fit using the test set observations to provide a final independent assessment of its predictive performance.⁴

As usual, remember that this recipe is just a guideline. You might find that it makes more sense to choose your single predictive fit using a metric other than predictive performance (such as domain knowledge, interpretability, or computational accessibility), or you may want to exclude some fits from consideration for some reason (be sure to document your reasons!).

Let’s demonstrate this process for our continuous response Ames house price and binary response online shopping purchase intent prediction projects.

13.1.1 Choosing a Single Fit for the Ames House Price Prediction Project

Example code for implementing the analysis in this section can be found in the 07_prediction_combine.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the online supplementary GitHub repository.

In Chapter 12, we found that the continuous response RF algorithm delivered the best validation set predictive performance results when comparing each of the algorithms trained on the default cleaned and preprocessed version of the Ames house price training dataset. However, the question remains: Does the RF algorithm remain dominant when we explore the fits trained across a range of alternative versions of the cleaned and preprocessed data? Let’s find out!

Table 13.1 shows the validation set correlation, root-mean squared error (rMSE), and mean absolute error (MAE) performance for the top 10 PCS predictive fits (in terms of the validation set rMSE value) from among the 2,016 total PCS predictive fits that we trained. These 2,016 fits are based on the six continuous response predictive algorithms (LS, LAD, lasso, ridge, and RF), each trained using 336 alternative versions of the cleaned/preprocessed Ames training dataset that arose from the different combinations of the following seven cleaning/preprocessing judgment calls for the Ames housing data:⁵

• Categorical format (numeric, simplified dummy, or dummy): Whether to convert ordered categorical variables to dummy variables, numeric variables, or a simplified version of the dummy variables.

• Number of neighborhoods (10 or 20): The number of neighborhoods to keep (the remaining neighborhoods are aggregated into an “other” category).

• Simplify variables (yes or no): Whether to simplify several variables.

• Imputation method (mode or other): Whether to impute missing categorical values with the mode (most common value) or to create an “other” category.

• Identical values threshold (0.65, 0.8, or 0.95): The threshold for the proportion of identical values above which variables are removed.

• Response transformation (none, log, or sqrt): Whether to apply a log- or square root-transformation to the response.

• Correlation feature selection threshold (0 or 0.5): The threshold for correlation-based feature selection. A threshold of 0 corresponds to no correlation-based feature selection and a threshold of 0.5 removes all features whose correlation with the response is less than 0.5.

Table 13.1: The algorithms, cleaning/preprocessing judgment calls, and corresponding validation set correlation, rMSE, and MAE values (rightmost columns) for the top 10 algorithms (defined in terms of the validation set rMSE value) from among all the cleaning/preprocessing judgment call–perturbed versions of the LS, LAD, lasso, ridge and RF fits for predicting house price in Ames

	Judgment calls							performance
Algorithm	Categorical format	Number of nbhds.	Simplify variables	Imputation method	Identical values threshold	Response transformation	Correlation selection threshold	Correlation	rMSE	MAE
LAD	dummy	20	no	mode	0.95	sqrt	0	0.970	16,738	11,920
LAD	dummy	20	no	other	0.95	sqrt	0	0.970	16,899	12,091
LS	dummy	20	no	other	0.95	sqrt	0	0.970	17,009	12,194
LS	dummy	20	no	mode	0.95	sqrt	0	0.970	17,020	12,183
Lasso	dummy	20	no	other	0.95	sqrt	0	0.969	17,249	12,229
LAD	numeric	20	no	mode	0.95	sqrt	0	0.968	17,296	12,273
LAD	numeric	20	no	other	0.95	log	0	0.969	17,372	12,213
LAD	numeric	20	no	mode	0.95	log	0	0.969	17,421	12,205
Lasso	dummy	20	no	mode	0.95	sqrt	0	0.968	17,426	12,284
LAD	numeric	20	no	other	0.95	sqrt	0	0.967	17,445	12,339

Note that while some of these judgment calls involve removing columns, none of them involve removing any rows (observations), which means that our predictive performance evaluations will be comparable across each of our predictive fits.

Even though the RF algorithm yielded the best performance for the original default cleaned/preprocessed version of the Ames dataset that we had used for our predictability analyses in Chapter 12, you may be surprised to observe that none of the top 10 fits shown in Table 13.1 involve the RF algorithm.

In addition, unlike the default cleaned/preprocessed version of the Ames data that we used for our predictability evaluations in Chapter 12, each of the top 10 fits presented here involve a square-root or log transformation of the response variable.

The fit with the best validation set predictive performance in Table 13.1 is the LAD algorithm trained on the version of the training data that has been cleaned/preprocessed so that the ordered categorical variables are converted to one-hot encoded “dummy” variables format (categorical format = “dummy”); all neighborhoods smaller than the top 20 neighborhoods are aggregated into an “other” neighborhood (number of neighborhoods = 20); there is no simplification of the porch, bathroom, and other variables (simplify variables = “no”); missing categorical values are imputed with the “mode” category (imputation method = “mode”); the identical values threshold is set to 0.95 (identical values threshold = 95); the response variable is square root–transformed (response transformation = “sqrt”); and there is no correlation feature selection implemented (correlation threshold = 0). This is the PCS predictive fit that will correspond to our “single best fit.”

13.1.1.1 The Test Set Assessment

After choosing our single fit (the LAD algorithm with the best validation set predictive performance), it’s time to provide a final independent assessment of its performance. Recall that because we have now used the validation set to choose this final fit, the predictions that it produces are now considered to be dependent on the validation set. As a result, the validation set performance evaluation is no longer considered reflective of the algorithm’s performance on actual future data, so we must now use the test set to conduct a final evaluation.

Table 13.2 shows the test set correlation, rMSE, and MAE performance measures of the chosen fit (the LAD fit based on the training set that was cleaned and preprocessed using the judgment calls specified in the first row of Table 13.1). Notice that the performance on the test set is slightly worse than the performance on the validation set (the correlation is slightly lower, and the rMSE and MAE are slightly higher), which is expected. Fortunately, the test set performance is still very good.

Table 13.2: The test set correlation, rMSE, and MAE performance metrics computed for the predictions generated by the LAD algorithm trained on the combined training set cleaned and preprocessed based on the best (as determined by the validation set) combination of judgment calls

Fit type	Evaluation set	Correlation	rMSE	MAE
LAD	Test set	0.969	18,164	12,835

Since this test set evaluation is designed to be a final evaluation of the chosen fit, it is recommended that you do not continue tweaking your fits to try and improve this performance assessment (this was the validation set’s job). We thus recommend that you avoid using your test set until you are confident that you are finished computing and modifying your predictive fits. As soon as you start trying to tweak your fits specifically to improve the test set performance, your test set will no longer be able to give you a realistic assessment of how your fit will perform on actual future data, and you must therefore find some additional data to use for final evaluations.

13.1.2 Choosing a Single Fit for the Online Shopping Purchase Intent Project

Let’s now turn to the online shopping binary response project.

R code for implementing the analysis we present in this section can be found in the 05_prediction_combine.qmd (or .ipynb) file in the online_shopping/dslc_documentation/ subfolder of the online supplementary GitHub repository.

The process of choosing a fit using PCS for the binary online shopping purchase intent project is fortunately very similar to the process that we just demonstrated for the continuous Ames house price project. The cleaning/preprocessing judgment call options that we considered for the online shopping dataset are

• Categorical format (numeric or categorical): Whether to convert the categorical variables to ordered numeric variables.

• Month format (numeric or categorical): Whether to convert the “month” numeric variable to a categorical variable.

• Log page (yes or no): Whether to apply a log-transformation to the page-type predictor variables.

• Remove extreme (yes or no): Whether to remove the extreme sessions (which we defined fairly arbitrarily as visiting more than 400 pages in a single session or spending more than 12 hours on a product-related page in a single session) that may be bots.

Table 13.3 shows the validation set accuracy, true positive rate, true negative rate, and area under the curve (AUC) performance for each of the top 10 predictive fits (in terms of the AUC value) for each of the three binary response algorithms (LS, logistic regression, and RF) trained on the \(2^4 = 16\) versions of the cleaned/preprocessed training data.

Table 13.3: The validation set accuracy, true positive rate, true negative rate (each based on the 0.161 prediction threshold value), and AUC for the top 10 algorithms (in terms of the validation set AUC) from among all the cleaning/preprocessing judgment call-perturbed versions of the LS, logistic regression, and RF fits for predicting online shopping purchase intent

	Judgment calls				performance
Algorithm	Categorical format	Month format	Log page	Remove extreme	Accuracy	True positive rate	True negative rate	AUC
RF	numeric	categorical	no	yes	0.855	0.884	0.850	0.938
RF	numeric	categorical	yes	yes	0.853	0.884	0.848	0.937
RF	categorical	categorical	yes	yes	0.850	0.892	0.842	0.937
RF	categorical	categorical	no	no	0.851	0.878	0.846	0.937
RF	numeric	categorical	no	no	0.849	0.886	0.843	0.937
RF	numeric	categorical	yes	no	0.852	0.884	0.846	0.936
RF	categorical	categorical	yes	no	0.852	0.892	0.845	0.936
RF	categorical	categorical	no	yes	0.847	0.886	0.840	0.936
RF	numeric	numeric	no	no	0.848	0.886	0.842	0.936
RF	numeric	numeric	no	yes	0.849	0.881	0.843	0.936

As in previous chapters, when calculating the accuracy, true positive rate, and true negative rate, we used a binary thresholding response prediction cutoff of 0.161 (based on the proportion of positive/purchase class observations in the training data).

From Table 13.3, the predictive fit that achieves the highest validation set AUC and accuracy values is the RF algorithm that was trained using the cleaned/preprocessed version of the training data where the unordered categorical variables are converted to a numeric format (categorical format = “numeric”), the month variable is kept in a categorical format (month format = “categorical”), no log-transformation is applied to the “page-related” variables (log page = “no”), and the extreme bot-like observations are removed (remove extreme = “yes”).

However, since alternative options for each of these cleaning/preprocessing judgment calls yield very similar validation set predictive performance, this indicates that these judgment calls do not seem to have much impact on the predictive performance.

13.1.2.1 The Test Set Assessment

Since we have now used the validation set to choose this top PCS predictive fit, we will perform a final independent assessment of this RF fit using the relevant cleaned/preprocessed version of the test set. The results are shown in Table 13.4. Again, the test set performance is slightly worse than the validation set performance.

Table 13.4: The test set accuracy, true positive rate, true negative rate, and AUC performance measures computed for the predictions (computed using the 0.161 threshold) generated by the “single best fit” based on the RF algorithm

Fit type	Evaluation set	Accuracy	True pos. rate	True neg. rate	AUC
RF	Test set	0.83	0.848	0.827	0.924

13.2 Approach 2: PCS Ensemble

Increasingly, one of the most common formats of the “final” predictive algorithm is to combine multiple accurate algorithms into an ensemble. We’ve already introduced the idea of ensembles in the context of the RF algorithm. In the case of RF, each base learner of the ensemble has the same type (a CART decision tree). However, there is no reason why we can’t create an ensemble of different types of algorithms, for example, by combining LS, LAD, ridge, lasso, and RF fits.

By creating an ensemble of several different PCS predictive fits, we can combine the different patterns that are being captured across the individual fits. It seems plausible that by combining multiple plausible predictions, you might be able to improve the predictive performance (this is sometimes the case even when the individual base learners themselves have poor predictive performance). Before creating an ensemble, however, we conduct predictability screening to ensure that we include only the best-performing fits in our ensemble (e.g., the 10 percent of fits with the best validation set performance). The precise format of the predictability screening must be determined separately for each domain problem and is typically based on domain knowledge.

A PCS ensemble generates a prediction for a new (future) data point by generating a separate prediction for each of the individual predictive fits that are to be included in the ensemble (i.e., that pass a relevant predictability screening) and combining their predictions into a single value. As with the RF ensemble algorithm, a final prediction could be computed based on the average of continuous response predictions or the majority vote prediction for binary response predictions. Note that for binary response problems, since the different binary response prediction algorithms may produce noncomparable unthresholded class probability predictions (i.e., the unthresholded LS predicted response does not have exactly the same meaning as the unthresholded logistic regression predicted response or the RF predicted positive class probability), we do not recommend combining binary response class probability predictions from different algorithms. Instead, we suggest directly computing binary predictions using a majority vote from across the ensemble members’ binary response predictions. Performance measures that require a probability prediction (such as AUC) can then be computed from the proportion of the ensemble fits that provide a positive prediction.

Figure 13.2(a) shows the process of predictability screening for a continuous response PCS ensemble using four algorithms (LS, LAD, RF, and ridge) each trained on two different versions of the cleaned/preprocessed training data (corresponding to a total of eight fits). In this example, we retain the top 50 percent of the fits (in terms of the validation set correlation performance measure) to include in the ensemble. Figure 13.2(b), shows the process of computing a continuous response prediction using the ensemble for a new data point based on the fits that passed the predictability screening.

Figure 13.2: The ensemble approach. The ensemble is built using four continuous response algorithms (LS, LAD, RF, and ridge), each trained on two alternative versions of the cleaned and preprocessed training dataset. This diagram portrays (a) the predictability screening process that determines which fits will be included in the PCS ensemble (in this example, the predictability screening step filters out the worst-performing 50 percent of the fits in terms of the correlation performance measure) and (b) the process of generating a prediction for a new response based on the resulting PCS ensemble.

The process of creating an ensemble involves:

1. Predictability screening: Identify which fits will be included in the ensemble.

   1. Create and document several different versions of the cleaned and preprocessed training, validation, and test sets using a range of combinations of cleaning and preprocessing judgment calls. Let \(K\) denote the number of cleaned/preprocessed datasets you end up with.

   2. Train each relevant predictive algorithm (e.g., LS, RF, etc.) using each of the \(K\) cleaned/preprocessed versions of the training data. If you have \(L\) different algorithms, then you will end up with \(K \times L\) different predictive fits.

   3. Using each of the \(K \times L\) predictive fits, generate a response prediction for each validation set observation.⁶

   4. Evaluate the validation set predictive performance for each of the \(K \times L\) fits (e.g., using rMSE or correlation for continuous responses and accuracy or AUC for binary responses).

   5. Conduct predictability screening by keeping only the best fits (say, the top 10 percent) in terms of validation set predictive performance. This threshold (e.g., the top 10 percent of fits) can be based on domain knowledge or it can be tuned using the ensemble’s predictive performance on the validation set.

2. Compute predictions for new observations using the ensemble: Predictions from the ensemble can be computed based on the fits that pass the predictability screening step (e.g., the top 10 percent of fits) by averaging their continuous predicted responses or taking the majority class of their binary predicted responses.

3. Test set evaluation: Evaluate your ensemble’s predictive performance using the test set observations to provide a final independent assessment of its predictive performance.

Note that if you want to tune the predictability screening threshold (e.g., identify the value of \(x\) in the top \(x\) percent of fits that lead to the best predictive performance), you must do so using the ensemble’s validation set predictive performance (i.e., do not use the test set to tune the predictability screening threshold since this will render it unable to provide a final independent performance assessment of your ensemble).

13.2.1 The Ensemble for the Ames House Price Project

Example code for implementing the analysis in this section can be found in the 07_prediction_combine.qmd (or .ipynb) file of the ames_houses/dslc_documentation/ subfolder of the online supplementary GitHub repository.

For the continuous response Ames house price prediction project, we have five different algorithms and 336 different cleaning/preprocessing judgment call combinations (a total of 1,680 fits).

Figure 13.3 shows the distribution of the validation set rMSE performance measure for these 1,680 predictive fits. We have placed a vertical line to demonstrate which fits have a rMSE validation performance in the top 10 percent (recall that the lower the rMSE, the better the predictive performance). We will create our ensemble using only these 168 fits whose rMSE values are to the left of this line.

Figure 13.3: A histogram showing the distribution of the validation set rMSE performance values across all LS, LAD, lasso, ridge, and RF fits across each of the cleaning/preprocessing judgment call–perturbed training sets. We have placed a vertical line demonstrating the best 10 percent of fits in terms of rMSE.

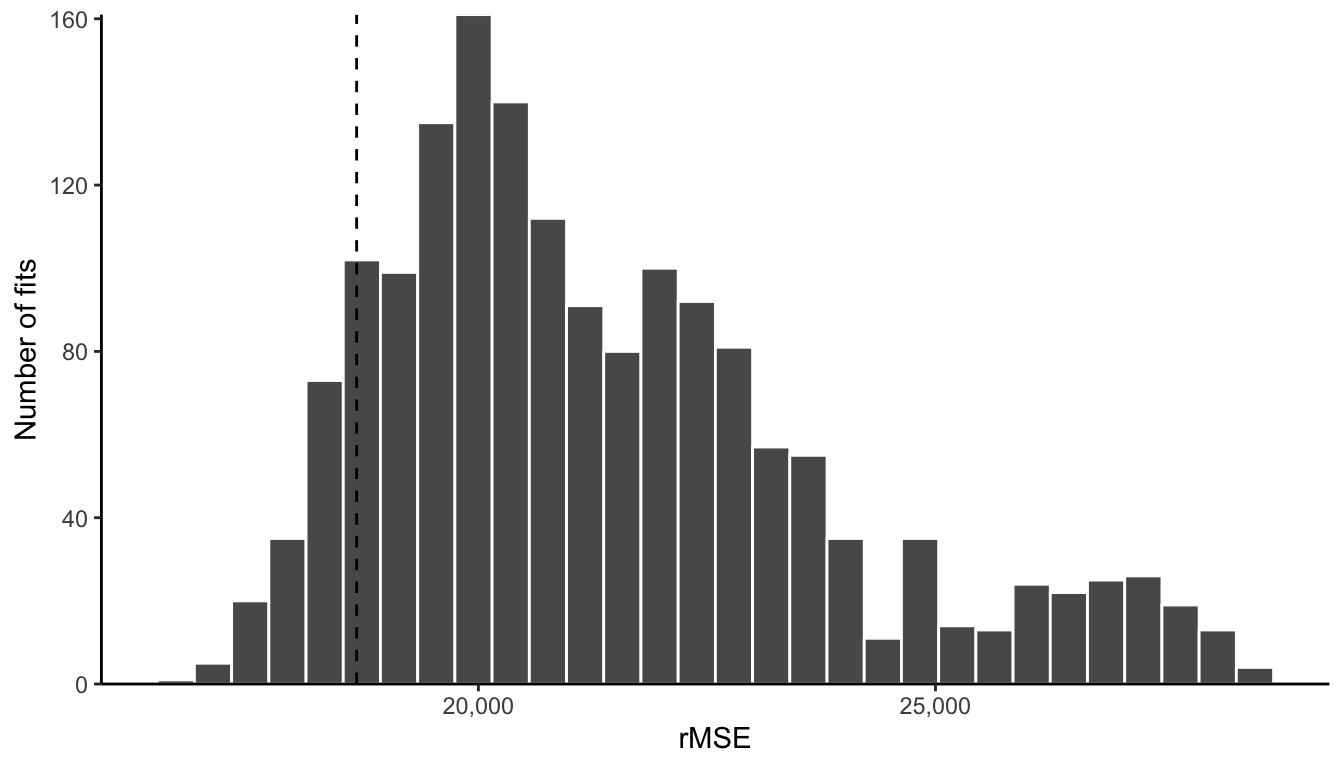
In Table 13.5, we can see the correlation, rMSE, and MAE values for the ensemble on the test set. Interestingly, the test set performance of the ensemble is slightly worse than the single LAD fit from approach 1, whose performance was shown in Table 13.2 (but this may not always be the case—there may be other scenarios in which the ensemble will perform better). Note that we should avoid tweaking our final ensemble to improve the test set performance since we have now used it for evaluation (unless we have additional data to use for further evaluation).

Table 13.5: The test set correlation, rMSE, and MAE performance measures computed for the PCS ensemble algorithm, where each member of the ensemble passed a predictability screening that filtered to the 10 percent of fits with the smallest validation set rMSE

Fit type	Evaluation set	Correlation	rMSE	MAE
Ensemble	Test set	0.968	18,441	13,106

13.2.2 The Ensemble for the Binary Online Shopping Project

Example code for implementing the analysis in this section can be found in the 05_prediction_combine.qmd (or .ipynb) file in the online_shopping/dslc_documentation/ subfolder of the supplementary GitHub repository.

The process for computing an ensemble for the binary response online shopping project is very similar to that of continuous response problems. The binary response predictions for each fit will be computed based on a probability prediction threshold of 0.161 (as previously discussed) and a majority vote will be used to determine the ensemble’s binary response prediction (i.e., if more than half of the ensemble fits predict “purchase,” then the ensemble’s prediction will be “purchase”).

For this project, we have three binary algorithms to include in our binary response ensemble (LS, logistic regression, and RF) and just 16 cleaning/preprocessing judgment call combinations. Overall, our binary response ensemble will be substantially less complex than our continuous response ensemble, containing at most 48 fits.

To conduct predictability screening, Figure 13.4 shows the distribution of the validation set AUC across all 48 fits, where we have colored the bars based on which algorithm they correspond to. Recall that a higher AUC corresponds to better predictive performance. From Figure 13.4, it is very clear that the RF algorithm fits have substantially better performance than the LS and logistic regression fits. Based on these results, we will choose just the RF fits (which correspond to the top 33 percent of fits) to include in our ensemble.

Figure 13.4: A (stacked) histogram showing the distribution of the AUC values across all the cleaning/preprocessing judgment call–perturbed LS, logistic regression, and RF online shopping purchase intent predictive fits.

Table 13.6 shows the test set performance for the resulting ensemble majority vote predictions. Note that since the ensemble majority vote approach provides a binary prediction (rather than class probability predictions), we compute the AUC based on the proportion of ensemble member “votes” (predictions) that are for the positive class. Again, the test set performance of the ensemble is slightly worse than the single best RF fit that we selected in approach 1, whose performance was shown in Table 13.4.

Table 13.6: The test set accuracy, true positive rate, true negative rate, and AUC performance metrics computed for the predictions generated by the ensemble algorithm consisting of the RF fits trained on several versions of the cleaned/preprocessed training data

Fit type	Evaluation set	Accuracy	True pos. rate	True neg. rate	AUC
Ensemble	Test set	0.83	0.854	0.826	0.858

13.3 Approach 3: Calibrated PCS Prediction Perturbation Intervals

Note that the PCS PPI approach introduced in this section is currently applicable only for continuous response problems. Although we can compute intervals for the predicted class probabilities for binary response prediction problems, we cannot compute the coverage of these intervals, so we cannot easily calibrate them, making them difficult to interpret.

While the ensemble approach of Section 13.2 takes into consideration several different potential versions of the response predictions for each observation, it still reports only one response prediction value for each data point. Rather than combining the alternative response predictions into just one number (“the house is predicted to sell for $143,000”), why not instead report an interval of plausible predictions for each response (e.g., “the house is predicted to sell between $141,000 and $152,000”)?

This is what PCS Prediction Perturbation Intervals (PPIs) do. PPIs correspond to an interval of plausible predictions from among the fits that pass a validation set predictability screening (where, as before, each fit corresponds to an algorithm trained on one particular version of the cleaned/preprocessed training data). There are many possible ways to decide which predictions are included in the interval, and here we will describe just one such approach for computing PPIs.

The predictability screening procedure for creating PPIs is the same as for the ensemble approach (e.g., filtering to just the top 10 percent of fits in terms of the validation set predictive performance, where this threshold should be chosen uniquely for each particular project).

However, after this initial predictability screening step, additional data perturbations (such as bootstrapping) are applied to each cleaned/preprocessed version of the training data that was involved in a fit that passed predictability screening. Each relevant algorithm is then retrained using the bootstrapped versions of each relevant cleaned/preprocessed training dataset, and an uncalibrated interval for a new data point can be computed from the range of resulting predictions.⁷ Note that you could make this process much simpler by skipping the bootstrapping step, but then the intervals that you compute will not convey any sampling uncertainty (i.e., the extent to which your results may differ had you used a slightly different dataset to train your algorithms).

Figure 13.5 depicts the process of (a) conducting predictability screening to identify which fits will be used to compute the PPIs, (b) retraining the fits that passed the predictability screening using multiple bootstrapped versions of the training data, and (c) computing a PPI for a new data point.

Figure 13.5: The PPI approach. This diagram depicts (a) the predictability screening process of determining which fits will be included in the PPI, (b) bootstrapping and retraining the fits that passed the predictability screening using three bootstrapped versions of the training data, and (c) generating an uncalibrated PPI for a new observation using the retrained fits.

By providing an interval of response predictions, a PPI can provide a sense of the uncertainty associated with the predictions for each observation. Specifically, by including bootstrapping, as well as alternative algorithms and cleaning/preprocessing judgment calls, a single PPI quantifies the uncertainty arising collectively from (1) the data collection process (via bootstrapping), (2) the cleaning/preprocessing judgment calls, and (3) the algorithmic choices.

A wider interval indicates that there is a higher level of uncertainty associated with the prediction, whereas a narrower interval indicates a lower level of uncertainty. However, using the prediction interval width as a comparable measure of uncertainty makes sense only if the intervals are calibrated in some way. If the intervals are not calibrated, simply by considering fewer fits when computing our interval, we may be able to produce a narrower interval of predictions, which might misleadingly indicate higher certainty in our predictions.

To be able to meaningfully calibrate our PPIs, we will need a fairly large number of predictions for each observation. Generating at least \(J = 100\) different bootstrapped predictive fits is traditionally recommended, however, this is not always computationally feasible. Although training each individual fit will not necessarily be computationally intensive (unless your dataset is particularly large), training hundreds or thousands of fits will quickly reach the computational limit of most personal laptops. For example, let’s say we start with \(K = 100\) cleaning/preprocessing judgment call combinations and \(L = 5\) algorithms, corresponding to a total of \(K \times L = 500\) fits before predictability screening and bootstrapping. If after predictability screening (where we take just the top 10 percent of fits) we have \(H = 0.1 \times K \times L = 50\) fits, then after computing just \(J = 10\) bootstrapped samples of each remaining cleaned/preprocessed training dataset and retraining the relevant algorithms using each bootstrapped training sample, we end up with a total of \(J \times H = 500\) fits that we must train to compute our interval (if, however, we had computed \(J = 100\) bootstrap samples, we would have \(5,000\) fits to compute, which is likely to be far too many for most laptops!). In this book, we will therefore stick with \(J = 10\) bootstrap samples (but we recommend computing more if you have the computational capacity).

13.3.1 Coverage and Calibration

Calibrating a collection of PPIs involves modifying them to have a prespecified coverage level. The coverage (Box 13.2) of a collection of intervals corresponds to how often the intervals cover (contain) the observed response. For instance, for the Ames house price project, if 70 percent of the sale price PPIs computed for the validation set houses contain the corresponding observed sale price, then the validation set coverage is 70 percent.

Box 13.2: Coverage

The coverage of a collection of PPIs corresponds to the proportion of the intervals that contain the observed response.

Typically, we will aim for 90 or 95 percent coverage.⁸ If we are aiming for 90 percent coverage, we will typically use the 0.05 and 0.95 quantiles (\(q_{0.05}\) and \(q_{0.95}\), respectively) of the response predictions for a given data point to compute the initial uncalibrated PPI for the data point, which corresponds to the following interval:

\[[q_{0.05}, ~q_{0.95}].\]

Note that if the perturbed fits included in our intervals were capturing all of the associated sources of uncertainty, then this \([q_{0.05}, ~q_{0.95}]\) interval would have 90 percent coverage.⁹ However, unfortunately, since our perturbations are rarely able to capture all the uncertainty associated with our predictions, the actual coverage that we obtain in practice from a \([q_{0.05}, ~q_{0.95}]\) interval will typically be lower than 90 percent. This is where calibration comes in (Box 13.3): by increasing (or decreasing) the length of each interval, we can create calibrated intervals that achieve our desired coverage level of 90 percent.

For a given data point, the length of the original uncalibrated interval is \(q_{0.95} - q_{0.05}\). To calibrate our intervals to have a coverage of 90 percent, we want to identify the value of a constant, \(\gamma\), that can be used to multiplicatively expand (or contract) the length of the intervals to \(\gamma(q_{0.95} - q_{0.05})\) such that 90 percent of these calibrated intervals will contain the corresponding observed response values.

One possible formula for a calibrated PPI that will have length \(\gamma(q_{0.95} - q_{0.05})\) is

\[ [\textrm{median} - \gamma\times (\textrm{median} - q_{0.05}), ~~\textrm{median} + \gamma \times (q_{0.95} - \textrm{median})], \tag{13.1}\]

which is centered around the median prediction for the observation (the 0.5 quantile). To show that the length of this interval is indeed \(\gamma(q_{0.95} - q_{0.05})\), subtract the start point of the interval from the end point.

Note that if \(\gamma =1\), then the calibrated interval is identical to the original uncalibrated interval. To identify a value of \(\gamma\) that leads to a validation set coverage of 90 percent, we can try several values of \(\gamma\), compute the validation set coverage for each choice, and select the value of \(\gamma\) that yields a validation set coverage closest to 90 percent.

Box 13.3: PPI Calibration

One way to calibrate the PPIs to achieve a particular coverage is to choose a multiplicative factor, \(\gamma\), by which to expand or shorten the lengths of the intervals such that the modified intervals have a coverage of 90 percent. One possible formula for a set of calibrated PPIs is given by \[[\textrm{median} - \gamma\times (\textrm{median} - q_{0.05}), ~~\textrm{median} + \gamma \times (q_{0.95} - \textrm{median})].\] The value of \(\gamma\) is chosen by trying several possible values of \(\gamma\) and identifying which value yields a calibrated validation set PPI coverage closest to 90 percent.

To create a calibrated PPI for a new observation you can then plug the prediction quantiles (\(q_{0.05}\) and \(q_{0.95}\)), the median prediction value, and your chosen value of \(\gamma\) into Equation 13.1. (Note that you will be using the same value of \(\gamma\) for every interval.)

As a small example, if you have a data point whose response predictions range from 88 to 96, with \(q_{0.05} = 88.2\), \(q_{0.95} = 94.9\), and a median of \(91.5\), and you have chosen \(\gamma = 1.23\), then the original uncalibrated PPI is \([q_{0.05}, q_{0.95}] = [88.2, 94.9]\) and the calibrated PPI for this data point will be

\[ \begin{align*} [&\textrm{median} - \gamma\times (\textrm{median} - q_{0.05}), ~~\textrm{median} + \gamma \times (q_{0.95} - \textrm{median})] \\ & ~~~= [91.5 - 1.23 \times (91.5 - 88.2), ~91.5 + 1.23 \times (94.9 - 91.5) ] \\ &~~~= [87.4,~ 95.7], \end{align*} \]

which is slightly wider. You can interpret this as: for 90 percent of your data points, the response should fall in the given calibrated interval, which for this particular data point, is \([87.4,~ 95.7]\). Each individual data point will have its own calibrated interval.

Since you have now used the validation set for numerous tasks (including prediction screening and calibrating the PPIs), a final estimate of the coverage of the calibrated intervals should then be conducted using the test set.

13.3.2 Computing Prediction Perturbation Intervals

Let’s wrap up this section with a summary of the process of computing calibrated PPIs (recall that this is just one suggested approach for computing PPIs—there are many possible ways to incorporate the perturbations when forming an interval). Note that the predictability screening step is the same as for the ensemble approach:

1. Predictability screening: Identify which fits will be included in the interval.

   1. Create and document several different versions of the cleaned and preprocessed training, validation, and test sets using a range of combinations of cleaning and preprocessing judgment calls. Let \(K\) denote the number of cleaned/preprocessed datasets you end up with.

   2. Train each relevant predictive algorithm (e.g., LS, RF, etc.) using each of the \(K\) cleaned/preprocessed versions of the training data. If you have \(L\) different algorithms, then you will end up with \(K \times L\) different predictive fits.

   3. Using each of the \(K \times L\) predictive fits, generate a response prediction for each validation set observation.¹⁰

   4. Evaluate the validation set predictive performance for each of the \(K \times L\) fits (e.g., using rMSE or correlation for continuous responses).

   5. Conduct predictability screening by keeping only the best fits (say, the top 10 percent) in terms of validation set predictive performance.

2. Conduct bootstrap perturbations and retrain each relevant fit:¹¹

   1. Create \(J\) bootstrapped, data–perturbed versions of each of the cleaned/preprocessed datasets that were involved in fits that passed the predictability screening.

   2. Retrain each of the fits that passed the predictability screening using each of the \(J\) bootstrapped versions of the relevant cleaned/preprocessed training datasets. If \(x \times K \times L\) fits passed the predictability screening (where \(x\) corresponds to the proportion of fits that passed the predictability screening; \(0 < x \leq 1\) and \(x = 0.1\) corresponds to selecting the top 10 percent of fits), then you will end up with \(x \times J \times K \times L\) predictive fits (if this value is not an integer, you can round up to the nearest integer). We recommend ensuring that \(x \times J \times K \times L \geq 100\).

3. Calibrate the PPIs using the validation set:

   1. If you are aiming for \((1 - \alpha)\) percent coverage, first compute an uncalibrated interval for each validation set observation based on the \(\alpha/2\) and (\(1 - \alpha/2\)) quantiles of the predictions: \([q_{\alpha/2}, ~q_{(1 - \alpha/2)}]\).

   2. Estimate the coverage of your uncalibrated validation set intervals by computing the proportion of the intervals that contain the observed response.

   3. Identify the calibration constant, \(\gamma\), the magnitude by which you need to lengthen or shorten the intervals to achieve a validation set coverage of \((1-\alpha)\) percent. This can be done by computing the coverage of the calibrated intervals using \[[\textrm{median} - \gamma\times (\textrm{median} - q_{\alpha/2}), ~~\textrm{median} + \gamma \times (q_{(1-\alpha/2)} - \textrm{median})]\] for various values of \(\gamma\).

4. Compute calibrated PPIs for new data points: Computing calibrated PPIs for new data points involves computing the response prediction using each of the \(x \times J \times K \times L\) bootstrapped fits that pass the predictability screening, identifying the \(\alpha/2\) and \((1 - \alpha/2)\) quantiles (\(q_{\alpha/2}\) and \(q_{(1 - \alpha/2)}\)) of these predictions, and plugging these quantiles and the value of \(\gamma\) identified in the previous calibration step into the calibrated PPI equation: \[[\textrm{median} - \gamma\times (\textrm{median} - q_{\alpha/2}), ~~\textrm{median} + \gamma \times (q_{(1-\alpha/2)} - \textrm{median})].\]

5. Test set evaluation: Compute calibrated PPIs for each test set observation and compute their coverage.

13.3.3 Perturbation Prediction Intervals for the Ames House Price Project

Example code for implementing the analysis in this section can be found in the relevant 07_prediction_combine.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the online supplementary GitHub repository.

To produce PPIs for the continuous response Ames house price prediction project, we used the 168 fits (each corresponding to an algorithm trained on a particular cleaned/preprocessed version of the training data) that passed predictability screening corresponding to the fits whose validation set performance was in the top 10 percent. For each of these fits, we computed \(J = 10\) different bootstrap samples of the cleaned/preprocessed training dataset and retrained each relevant algorithm using each of the 10 bootstrapped training datasets, resulting in a total of 1,680 perturbed fits, which will be used to produce the intervals. Note that we were able to compute these fits in parallel on a reasonably powerful laptop, but computing this many fits may be too computationally intensive for less powerful laptops.

After creating an uncalibrated PPI for each validation set observation based on the 5th and 95th prediction quantiles from the 1,680 fits, we computed the uncalibrated validation set coverage to be 60.8 percent (meaning that only 60.8 percent of the uncalibrated validation set intervals contained the observed sale price, which is substantially lower than the 90 percent that we were aiming for).

Setting \(\gamma = 2.04\) (i.e., slightly more than doubling the length of each interval), and computing the calibrated intervals based on

\[[\textrm{median} - 2.04 (\textrm{median} - q_{0.05}), ~~\textrm{median} + 2.04 (q_{0.95} - \textrm{median})],\]

where “median” is the median prediction for the given observation, and \(q_{0.05}\) and \(q_{0.95}\) are the 5th and 95th quantiles of the predictions for the given observation, we increased the validation set coverage to 90 percent, which is our target coverage.

Recall that the prediction stability plots that we produced in Chapter 10 and Chapter 12 provided us with a way of visualizing the range of predictions we produced across various perturbations. In Chapter 10 and Chapter 12, however, we were originally using these prediction stability plots to visualize just one source of uncertainty at a time (e.g., exploring uncertainty in the data collection process via data perturbations or exploring uncertainty in the cleaning/preprocessing process via cleaning/preprocessing judgment call perturbations). The PPIs, however, portray many sources of uncertainty in a single interval. Figure 13.6 shows a prediction stability plot of the 90 percent coverage-calibrated PPIs for 150 randomly selected validation set houses. Approximately 90 percent of the intervals should cross the diagonal line, indicating that they contain the observed response (we used red to visually highlight the intervals in Figure 13.6 that do not cover the observed response).

Figure 13.6: A prediction stability plot showing the calibrated PPIs for a random sample of 150 validation set houses. The red intervals do not cover the observed sale price response.

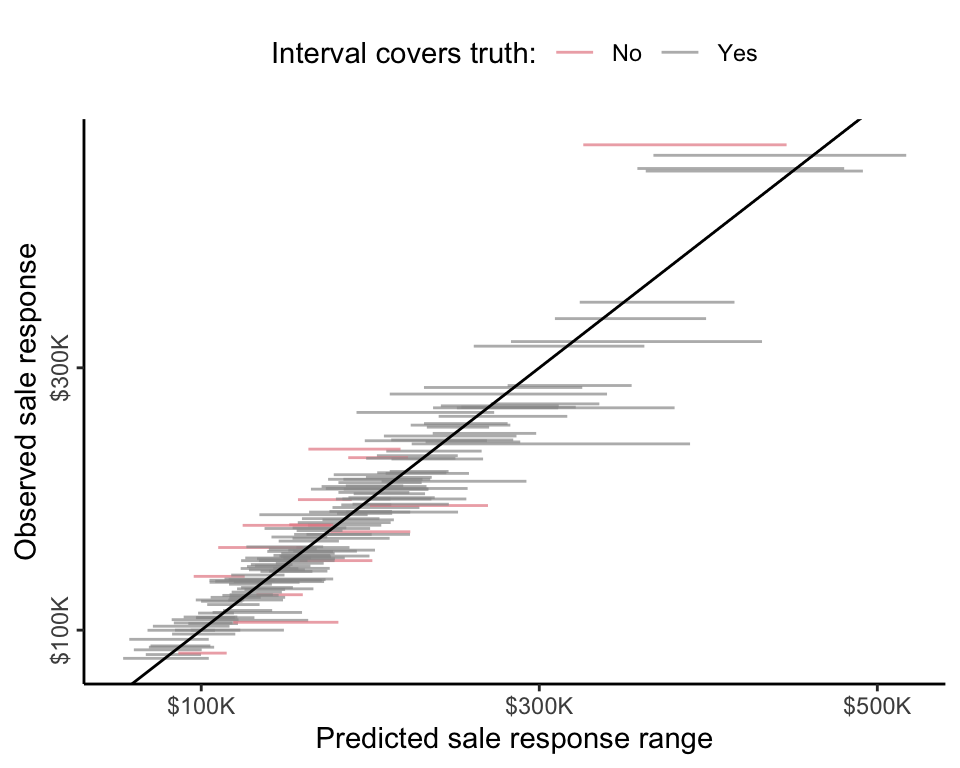
To give a final independent assessment of the coverage of our PPIs for new observations, we need to again turn to the test set. When we create calibrated PPIs for the test set houses (using the same calibration constant as above, \(\gamma = 2.04\)), the coverage is equal to 88 percent (i.e., 88 percent of the calibrated test set PPIs contain the observed response), which is fairly close to our goal of 90 percent.

Recall that we currently recommend computing PPIs for continuous response predictions only. The development of PPIs for binary response problems is an area of ongoing research in the Yu research group.

13.4 Choosing the Final Prediction Approach

For continuous response prediction problems, we’ve provided three approaches for choosing the format of your final predictions:

• The single best fit

• The ensemble

• The PPI (currently available for continuous response problems only)

The most informative approach is the PPI approach (approach 3) since it not only provides predictions but it also conveys a sense of the uncertainty associated with the predictions in the form of a calibrated interval. For continuous response prediction problems, the PPI approach is our recommended approach overall.

However, in many scenarios, you may need to provide only a single number as your final prediction. For binary response prediction problems as well as in these scenarios, we suggest choosing the approach (the single best fit or the ensemble fit) that yields the most accurate predictive performance on the validation set. However, if computability and interpretability are more critical considerations for your particular project, the single-best-fit approach will often be the best choice. As always, be sure to let the needs and requirements of your specific domain project guide your choice.

13.5 Using Your Predictions in the Real World

Once you have decided on the type of predictions to present (single fit, ensemble, or PPI), the next step is to make them available to those who want to apply them to new data for real-world decision making. However, many end-line users of predictive algorithms are nontechnical and may not have the skills required to use your code to input their own data into your algorithm. To ensure it is useful, you may need to build your algorithm into existing applications or create a user-friendly website/application where users can upload their data without needing to write any code.

However, most data scientists do not have the software engineering skills necessary to develop sophisticated applications or incorporate complex predictive fits into existing computational interfaces. Prototypes can be developed using interactive dashboards or “shiny” apps¹², but more advanced products based on predictive algorithms typically require the expertise of software engineers and ML engineers.

If your goal is to write a research paper about your predictive results in the context of a domain problem, we recommend making your code and documentation publicly available by hosting it in a public GitHub repository. This provides others with an avenue to use your work, which will not be possible if your algorithm is only summarized in the methods section of a research paper without any available code.

Exercises

True or False Exercises

For each question, specify whether the answer is true or false (briefly justify your answers).

1. In the PCS framework, the final predictive fit is chosen from among several algorithms, each trained on just one cleaned and preprocessed version of the training data.

2. The members of an ensemble algorithm must all be of the same type (e.g., they should all be LS algorithms).

3. The output of an ensemble algorithm provides just one prediction for each data point.

4. The same performance measures (e.g., correlation and rMSE for continuous response problems and accuracy, sensitivity, and AUC for binary response problems) can be used to evaluate and compare ensemble predictions and predictions from a single fit.

5. The predictive performance of an ensemble will always be better than the single best predictive fit.

6. After using the test set to evaluate the “final” fit, it is not a good idea to make further modifications to our fits in order to improve the test set performance.

7. By removing the largest and smallest 5 percent of predictions when creating PPIs (i.e., basing our intervals on the 5th and 95th prediction quantiles), we force the coverage of the intervals on the validation set to be equal to 90 percent.

8. Having trained your final predictive fit in R or Python, anyone will be able to use your fit to generate predictions if they have access to your code, regardless of their technical skill level.

9. If the top fits (in terms of the validation set predictive performance) include various alternative options for a particular cleaning/preprocessing judgment call, then the predictive performance is considered to be fairly stable (i.e., not sensitive) to this judgment call.

10. It is important to conduct predictability screening before creating PCS ensembles and PPIs.

Conceptual Exercises

11. Explain how the PCS single-fit approach that we introduced in this chapter is different from the traditional ML approach to choosing a single fit.

12. Explain in your own words how to train an ensemble predictive algorithm and how to use it to generate a prediction for a new data point.

13. Comment on the relationship between the PPIs introduced in this chapter and the prediction stability assessments that we conducted in previous prediction chapters (in which we produced various “prediction stability plots”).

14. For the Ames house price project, describe which of the three final prediction formats you would choose. Justify your choice.

15. Identify which sources of uncertainty are taken into account for each of the three final prediction formats that we introduced in this chapter (the single fit, ensemble, and PPI).

Coding Exercises

16. The file ames_houses/data/perturb_528458180.csv contains a set of data perturbed, cleaning/preprocessing judgment call perturbed, and algorithm–perturbed house price predictions for a single validation set house in Ames (PID 528458180) (we did not remove any fits during predictability screening). In this exercise, you will compute an ensemble prediction and a PPI for this house.

    1. Compute an ensemble prediction for the sale price of the house using all the predictions provided.

    2. Plot a histogram of the distribution of the sale price predictions for the house.

    3. Mark the location of the observed sale price of the house ($238,500) on your histogram using a colored vertical line (if you’re using ggplot2 in R, the geom_vline() function will be helpful for adding vertical lines).

    4. Mark the location of your ensemble prediction of the house’s sale price on your histogram using a different-colored vertical line.

    5. Compute an uncalibrated PPI for the house. Add vertical lines indicating the locations of the upper and lower bounds of this uncalibrated PPI (i.e., add vertical lines corresponding to the 0.05 and 0.95 quantiles of the predictions).

    6. Using the multiplicative factor of \(\gamma = 2.04\) (the choice of \(\gamma\) that we computed for the house price prediction problem in this chapter), compute a calibrated PPI for the house, and add dashed vertical lines indicating the upper and lower bounds of the calibrated PPI to your plot. Comment on what you observe.

17. Instead of calibrating the Ames house price PPIs using a multiplicative factor, \(\gamma\), in this exercise we will consider an alternative additive calibration approach that involves choosing a constant value to subtract from the lower bound of the interval and add to the upper bound of the interval. This additively calibrated interval is \([q_{0.05} - \zeta, ~q_{0.95} + \zeta]\). You may want to write your code for this exercise in the relevant section of the 07_prediction_combined.qmd (or .ipynb) file (right after the multiplicative calibration) in the ames_houses/dslc_documentation/ subfolder.

    1. Identify the value of \(\zeta\) that leads to additively calibrated intervals for the validation set houses that have coverage as close to 90 percent as possible.

    2. Using the value of \(\zeta\) that you identified in the previous part, compute an additively calibrated interval for the house from exercise 16 (PID 528458180). Compare your additively calibrated interval with your multiplicatively calibrated interval from exercise 16.

    3. Compute the corresponding additively calibrated intervals for the test set houses (using the same \(\zeta\) as before), and compare the coverage with the test set coverage of the original multiplicatively calibrated intervals. Which calibration approach performs better?

18. Based on the code in the 07_prediction_combined.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder (or by writing your own code), recompute the PPIs using several values for \(J\) (the number of bootstrap data perturbations) and \(x\) (the predictability screening proportion threshold–we originally considered \(x=0.1\) corresponding to the top 10 percent of fits). You can keep the set of algorithms (there are \(L\) algorithms) the same. Comment on how the lengths of the intervals and the uncalibrated validation set coverage of the intervals change as \(J\) and \(x\) increase/decrease. When choosing values of \(J\) and \(x\) to consider, keep in mind that larger values will be more computationally intensive.

19. Conduct some post hoc analyses of each type of prediction (single, ensemble, interval) computed in the 07_prediction_combined.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder. For example, can you identify whether there are any particular kinds of houses (e.g., large houses, houses in a particular neighborhood, etc.) whose sale price is hard to predict (i.e., tend to have high prediction errors)? You may want to write your post hoc analysis code in the relevant section at the end of the 07_prediction_combined.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder.

Project Exercises

20. Predicting happiness (continued) This project extends the continuous response happiness prediction project from the project exercises in Chapter 9, Chapter 10, and Chapter 12 based on the World Happiness Report data. The data for this project can be found in the exercises/happiness/data/ folder of the online supplementary GitHub repository.

    1. Explicitly identify the cleaning and preprocessing judgment calls that you made when cleaning/preprocessing the data (this will be easy if you documented them in your DSLC documentation), and discuss any reasonable alternative judgment call options that you could have made for each judgment call.

    2. In the 03_prediction.qmd (or .ipynb) code/documentation file in the relevant exercises/happiness/dslc_documentation/ subfolder, identify the fit that achieves the best validation set performance from among a range of LS, LAD, lasso, ridge, and RF algorithm happiness predictive fits, each trained on various versions of the training dataset that are cleaned and preprocessed according to several combinations of judgment call options.

    3. Evaluate your single best fit on the test set.

    4. Conduct predictability screening in preparation for computing ensemble predictions and PPIs.

    5. Compute ensemble predictions for the test set and provide an evaluation of your ensemble’s test set performance.

    6. Compute uncalibrated PPIs for the validation set data points, and compute the validation set interval coverage.

    7. Identify the multiplicative calibration constant, \(\gamma\), that yields a validation set PPI coverage of 90 percent.

    8. Compute calibrated ensemble predictions for the test set (using the \(\gamma\) constant value identified in part (g)), and compute the test set interval coverage.

    9. Discuss which of the three “final” prediction formats you prefer for this project.

21. Predicting patients at risk of diabetes (continued) This project extends the binary response diabetes risk prediction project from Chapter 11 and Chapter 12, based on the data from the 2016 release of the National Health and Nutrition Examination Survey (NHANES). The folder exercises/diabetes_nhanes/data/ contains the NHANES dataset.

    1. Explicitly identify the cleaning and preprocessing judgment calls that you made when cleaning/preprocessing the data (this will be easy if you documented them in your PCS documentation and code files), and discuss any reasonable alternative judgment call options that you could have made for each judgment call.

    2. In the 03_prediction.qmd (or .ipynb) code/documentation file in the relevant exercises/diabetes_nhanes/dslc_documentation/ subfolder, identify the fit that achieves the best validation set performance from among a range of LS, logistic regression, and RF algorithm predictive fits for diabetes, each trained on various versions of the training data that are cleaned and preprocessed according to different combinations of judgment call options.

    3. Evaluate your single best fit on the test set.

    4. Conduct predictability screening.

    5. Compute binary response ensemble predictions for the test set and provide an evaluation of your ensemble’s test set performance. Compare the ensemble’s performance with the single best fit algorithm’s performance.

---

1. Calibrating intervals of binary probability response predictions is an active area of research in the Yu research group.

2. Note that we are not including data perturbations (e.g., bootstrapping).

3. To generate a prediction using each fit, the validation set must be cleaned and preprocessed in the same way as the relevant cleaned/preprocessed training set.

4. The test set must be cleaned and preprocessed in the same way as the relevant cleaned/preprocessed training set that the selected fit is trained on.

5. Judgment call combinations that led to identical datasets were removed, leaving 336 unique cleaned/preprocessed datasets.

6. To generate a prediction using each fit, the validation set must be cleaned and preprocessed in the same way as the relevant cleaned/preprocessed training set.

7. Note that you do not need to apply bootstrapping to the new data points for which you are trying to compute an interval. The input data for each fit only needs to match the cleaned and preprocessed format of the training data, which is not affected by bootstrapping.

8. Why not aim for 100 percent coverage? Unless we can quantify every single source of uncertainty associated with our predictions, the only interval with true 100 percent coverage will be \([-\infty, \infty]\), which is not particularly useful.

9. This is similar to a 90 percent confidence interval in traditional statistical inference.

10. To generate a prediction using each fit, the validation set must be cleaned and preprocessed in the same way as the relevant cleaned/preprocessed training set.

11. Note that the bootstrap is just one possible type of perturbation that you can use; others include subsampling.

12. Shiny is a package that makes it easy to build interactive web apps straight from R & Python.