
7 Clustering
This is the Open Access web version of Veridical Data Science. A print version of this book is published by MIT Press. This work and associated materials are subject to a Creative Commons CC-BY-NC-ND license.
In Chapter 6, we used principal component analysis to create simplified low-dimensional representations of our data by summarizing and aggregating the variables (columns). In this chapter, we will shift our focus from the variables (columns) of the data to the observations (rows). Specifically, our goal in this chapter is to identify reasonable clusters of observations, and we will introduce several unsupervised learning clustering algorithms that can help us achieve this goal.
While you might be new to the idea of clustering in the context of data science, you have actually been solving real-world clustering problems your whole life. For instance, think about how you organize your book collection. Are your books organized by genre? By color? Alphabetically? What about your clothes? Do you organize them by function (e.g., are your socks and underwear stored separately from your shirts)? How are the objects in your kitchen organized? Unless you particularly enjoy chaos, you probably use various characteristics of the objects in your kitchen to determine how to group them. Your system might be imperfect, and some objects’ categories might be ambiguous (should the novel “2001: A Space Odyssey” fall under “classics” or “science fiction”? Should that weird, hybrid bowl-plate that your friend Jim gave you live with the bowls or the plates?), and before you started organizing, you probably didn’t know ahead of time which groups you were going to end up with, or even how many groups there would be. This process is incredibly subjective: the way that we might choose to organize our belongings will probably be different from how you would do it. There is usually no underlying “correct” set of groupings, but regardless of how you end up grouping your belongings, chances are that just the act of organizing objects into groups helps provide a big-picture sense of what the overall object ecosystem looks like.
This process is also helpful in the context of data. Since data contains many observational units (objects, people, events, etc.), to help understand what kinds of observational units your data contains it seems only natural to try to organize them into groups. The activity of organizing the observations in your data into groups is called clustering.
We generally think of a cluster in a dataset as a group of observations that are similar to one another (while also being dissimilar to the data points that are in other clusters). The definition of “similarity” here depends on the context or situation. How would you summarize the similarity between different objects in your kitchen? Perhaps you would define “similarity” based on how often the objects are used together, in which case a knife and a fork would have very high similarity but a fork and a blender would have fairly low similarity. Or perhaps you would base your definition on the objects’ frequency of use so that frequently used objects are considered more “similar” to one another than they are to infrequently used objects. There are typically many definitions of “similarity” that you could choose, and the same is true for observations in a dataset: you could base your definition on the Euclidean distance metric, the Manhattan distance metric, or a non-distance-based similarity measure, such as correlation.1
In this chapter, we will continue working with the nutrition dataset from Chapter 6. However, rather than considering each type of nutrient (such as the “Major minerals” nutrients or the “Vitamins” nutrients) separately, we will consider the full dataset that contains measurements across all nutrient groups. Recall that our overall goal for this project is to develop an app that will help people make more informed choices about the food they eat by providing concise and interpretable nutritional summaries of their meals. When we visualized the data in the principal component (PC) spaces, we saw glimpses of some underlying groupings of food items, such as fruits gathering in one portion of the plot and meats gathering in another. In this chapter, we will try to tease out these groups by identifying clusters of food items. Not only will this help us get a sense of what kinds of food items our dataset contains (which is very hard to do by just sifting through thousands of food descriptions), but it could also be used to help organize and categorize the food items contained in our app.
Since we typically don’t know in advance what clusters we will find in our data (i.e., there are usually no “ground truth” clusters), it is hard to evaluate whether the clusters we identify are correct. In the case of food items, perhaps we could try to use the US Department of Agriculture’s food groups as the ground truth. The current food groups are (1) fruits; (2) vegetables; (3) grains (cereals); (4) protein (meat, seafood, poultry); (5) dairy; and (6) confections. However, even these generally accepted food group definitions have a complex history. In 1943, seven food groups were proposed, which were soon reduced to four groups in 1956, before being expanded back to six groups, and eventually being shaped into the familiar “food pyramid” in the 1990s (Nestle 2013). These food groups clearly lack stability, and they certainly don’t represent a ground “truth.” Even if we did want to use these existing groups to organize our food items, doing so would require that we spend days manually assigning each of the thousands of food items in the data to a food group. This would be a challenging task, especially because these traditional food groups don’t even make sense for many of the food items in our data (what food group should “Pizza, cheese, from restaurant or fast food, thin crust” be in?)
At their core, these traditional food groups use nutritional content to group foods together. In this chapter, we will try to come up with our own food groups based on this idea, but rather than manually defining the food groups and labeling each food item, our goal is to create a data-driven algorithm that can automatically identify clusters of foods (and label each food item) for us. However, as with all data-driven results, these clusters will only be trustworthy if we can demonstrate that they are predictable and are stable to reasonable perturbations to the underlying data and judgment calls made throughout the data science life cycle (DSLC).
7.1 Understanding Clusters
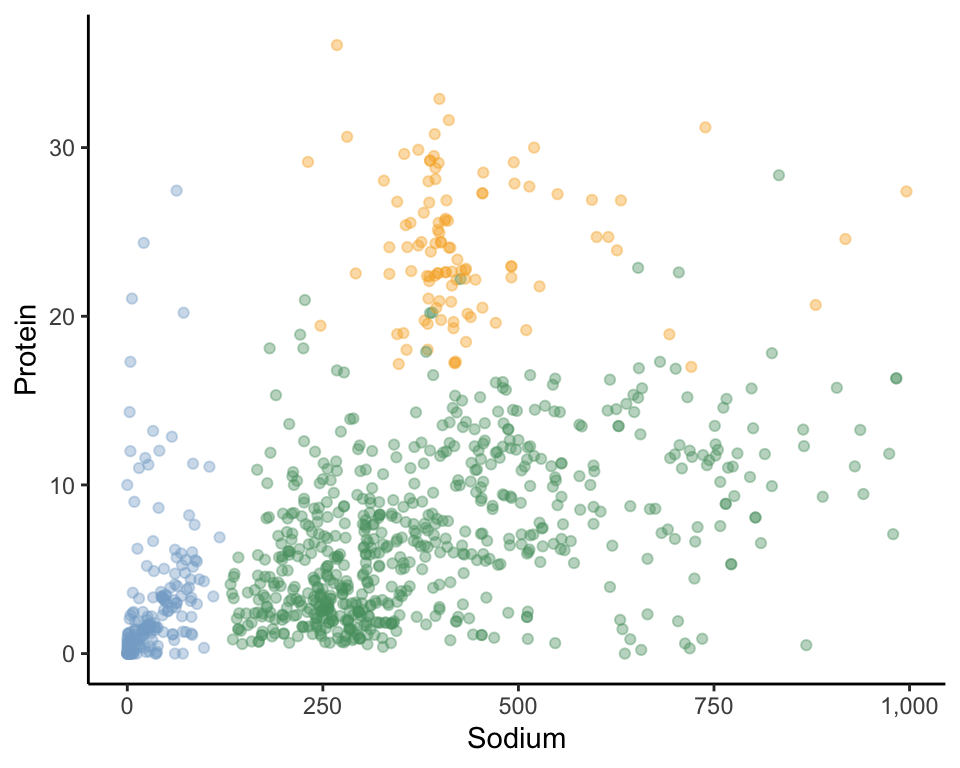
To formally introduce the idea of data-driven clusters, let’s consider an example from our food dataset based on just two nutrient variables: “sodium” and “protein.” Figure 7.1 displays 1,000 food items in the two-dimensional sodium-versus-protein scatterplot. Can you visually identify any groups of data points (i.e., data points that seem to be grouped together)? How many groups/clusters can you see?

One possible set of three clusters for this example is shown in Figure 7.2, where we visually indicate cluster “membership” (i.e., which cluster each observation belongs to) using color. Since visually identifying clusters is a subjective task, the clusters you saw may not match ours. Regardless of whether your three clusters were similar to ours, what made you want to group certain data points together into a cluster? To visually choose our clusters, we were looking for groups of data points that were close together, with a bit of a gap between them and the rest of the data points. We use this idea to define a cluster in Box 7.1.
7.1.1 Evaluating Clusters
The lack of a ground truth to compare our clusters to means that it doesn’t make sense to ask whether the clusters we identify are “correct”. However, we can still try to quantify the quality of a set of clusters based on cluster properties including:
Cluster tightness: How similar (or close together) points within each cluster are. Ideally, data points in the same cluster have high similarity.
Cluster distinctness: How similar (or close together) points in different clusters are. Ideally, data points in different clusters will have low similarity.
Cluster predictability: Whether the clusters reappear in new/external data and are capturing meaningful groups in the context of domain knowledge.
Cluster stability: Whether the clusters are stable across reasonable perturbations of the data, judgment calls, and algorithms.
We will expand on these measures of cluster quality in Section 7.5.
7.1.2 Defining Similarity
Having thrown around the term “similarity” fairly vaguely so far, let’s discuss what it means for two data points to be similar. When working with data, the definition of similarity is typically based on a similarity measure, which should be chosen based on domain knowledge and the context of the particular data problem that you’re working on. The most common similarity measures for clustering are based on distance metrics, such as the Euclidean distance or the Manhattan distance.2 The shorter the distance between two data points, the more similar they are.
Calculating the distance between two data points generally involves computing the differences between the individual measurements for each variable/column, and aggregating these differences in some way. However, just as for principal component analysis, if one of the variable’s measurements is on a larger scale than the other (e.g., “sodium” has values in the hundreds, which is on a much larger scale than “protein,” whose values are typically less than 20), then the variable with larger values will tend to dominate the distance calculation (recall the comparability principle from Section 5.3 of Chapter 5). If you want each variable to have equal influence on the distance calculation and the variables are not already on the same scale, then it is often a good idea to scale the variables (Box 7.2), such as by dividing each variable by its standard deviation (SD) or converting them to a common range (see Section 6.3 of Chapter 6). Keep in mind that standardization is not technically a requirement, and if the variables were originally on the same scale, scaling your variables might lead to misleading results.
Let’s examine two food items: (1) tuna pot pie and (2) an oatmeal cookie, both of whose SD-scaled sodium and protein content is displayed in Table 7.1. To quantify the similarity of these two food items, let’s look at how different the sodium and protein measurements are and then combine these differences.
| Food | Sodium | Protein |
|---|---|---|
| Tuna pot pie | 0.86 | 1.14 |
| Cookie, oatmeal | 1.20 | 0.79 |
7.1.2.1 The Manhattan (L1) Distance
The Manhattan distance (Box 7.3; also called the L1 distance for the mathematically inclined) between two food items involves calculating the absolute value of the difference between the individual nutrient measurements and adding all these differences together. For the tuna and cookie food items in Table 7.1, the Manhattan distance (\(d_1\)) is calculated as
\[\begin{align*} d_1(\textrm{tuna}, \textrm{cookie}) &= |0.86 - 1.2| + |1.14 - 0.79| \\ &= 0.34+ 0.35 \\ &= 0.69. \end{align*}\]
To write a general formula for the Manhattan distance between two data points with an arbitrary number of dimensions (variables), \(p\), we can denote the set of measurements for the two data points using the notation \(x_1 = (x_{1,1}, x_{1,2}, ..., x_{1,p})\) and \(x_2 = (x_{2,1}, x_{2,2}, ..., x_{2,p}\), where \(x_{i, j}\) is the \(j\)th variable’s measurement for the \(i\)th data point. A general formula for the Manhattan distance between two data points is then given by
\[ d_1(x_1, x_2) = \sum_{j = 1}^p |x_{1, j} - x_{2, j}|. \tag{7.1}\]
Intuitively, the Manhattan distance adds up the vertical and horizontal distances from one food item to the other, as shown in Figure 7.3.

Note that the Manhattan distance is named as such because it can be thought of as the driving distance between point A to point B along the grid-like streets of Manhattan in New York City (since you cannot travel by car directly as the crow flies).
7.1.2.2 The Euclidean (L2) Distance
Perhaps a more familiar notion of distance between two points is the length of the line that directly connects the two points, called the Euclidean distance, or L2 distance (Box 7.4). The Euclidean distance between the tuna pot pie and the oatmeal cookie data points in the two-dimensional sodium-protein space is shown in Figure 7.4.
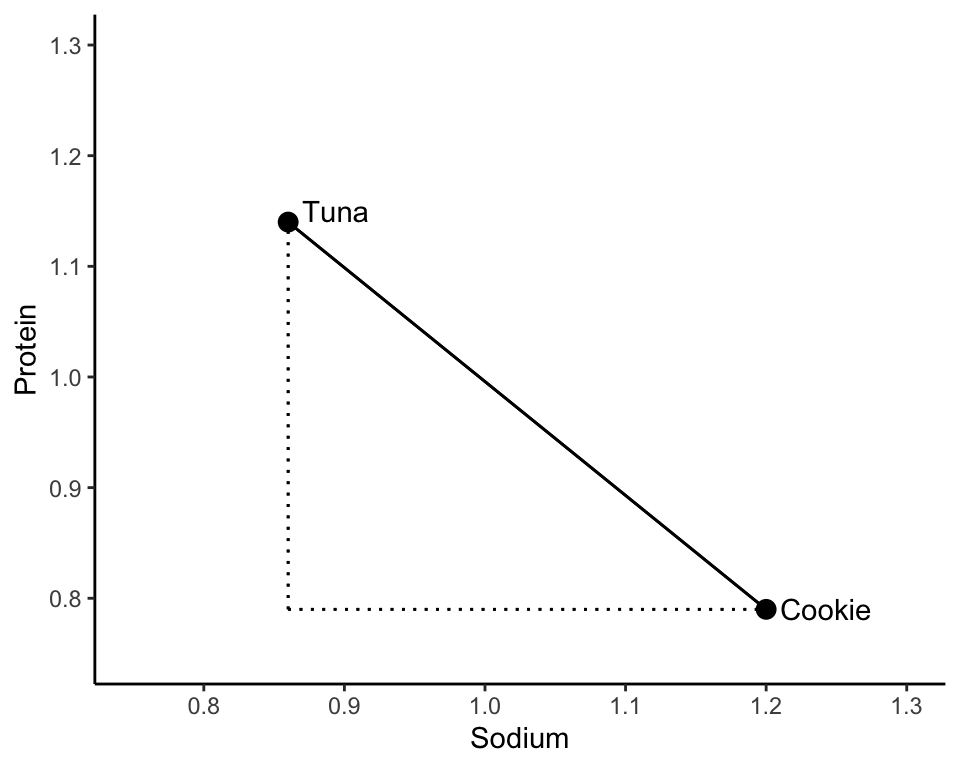
You might remember from high school that Pythagoras’ theorem says that the Euclidean distance between the tuna and cookie food items (from Table 7.1) can be computed as
\[\begin{align*} d_2(\textrm{tuna}, \textrm{cookie}) &= \sqrt{(0.86 - 1.2)^2 + (1.14 - 0.79)^2} \\ &= 0.49. \end{align*}\]
The general formula for the Euclidean distance, \(d_2\), for two data points, \(x_1\) and \(x_2\), each consisting of measurements for \(p\) variables, is then given by
\[ d_2(x_1, x_2) = \sqrt{\sum_{j = 1}^p (x_{1, j} - x_{2, j})^2}. \tag{7.2}\]
The definition of the similarity measure that you choose is a judgment call that should be informed by domain knowledge whenever possible. For instance, defining similarity using the Manhattan (L1) distance metric typically makes more intuitive sense if you want to tally up the individual differences across each dimension, as is sometimes the case for count data. However, for our SD-scaled nutrition measurements, the direct Euclidean (L2) distance feels more intuitive (the Euclidean distance is also more common). If you’re not sure which metric to use for your project, you can make a judgment call and investigate the downstream impacts of your choice. Perhaps your results will be stable across the choice of similarity measure, or perhaps one will lead to more meaningful results than the other.
7.2 Hierarchical Clustering
Now that we have a few options for measuring the similarity between data points, how can we use them to uncover clusters in our data? Recall that our goal is to find clusters of data points that are more similar to one another than they are to data points in other clusters. There are many ways that we could do this, such as the approach taken by the hierarchical clustering algorithm (Box 7.5), which involves iteratively merging clusters based on a similarity hierarchy.
Let’s define a data point’s cluster membership as a label that specifies which cluster it is in. The hierarchical clustering algorithm starts with every data point in its own cluster (i.e., every data point has a distinct cluster label). The first step involves merging the two most similar clusters (i.e., by giving them the same cluster label). Since each cluster consists of just one point at this initial stage, this step corresponds to merging the clusters of the two individual data points that are most similar to one another. The next step is to find the second most similar pair of clusters and merge them too, continuing this process until all the data points are in the same cluster. Since each step in this sequential iterative process involves reducing the number of clusters, by stopping at different points in the iterative process, you can generate various sets of clusters each with different numbers of total clusters. We will use \(K\) to denote the number of clusters that have been computed.
7.2.1 Defining Intercluster Similarity (Linkage Methods)
This hierarchical clustering algorithm involves iteratively merging the clusters of the most similar pairs of clusters. From Section 7.1.2, we know what it means for two data points to be similar to one another, but what does it mean for a pair of clusters to be similar to one another?
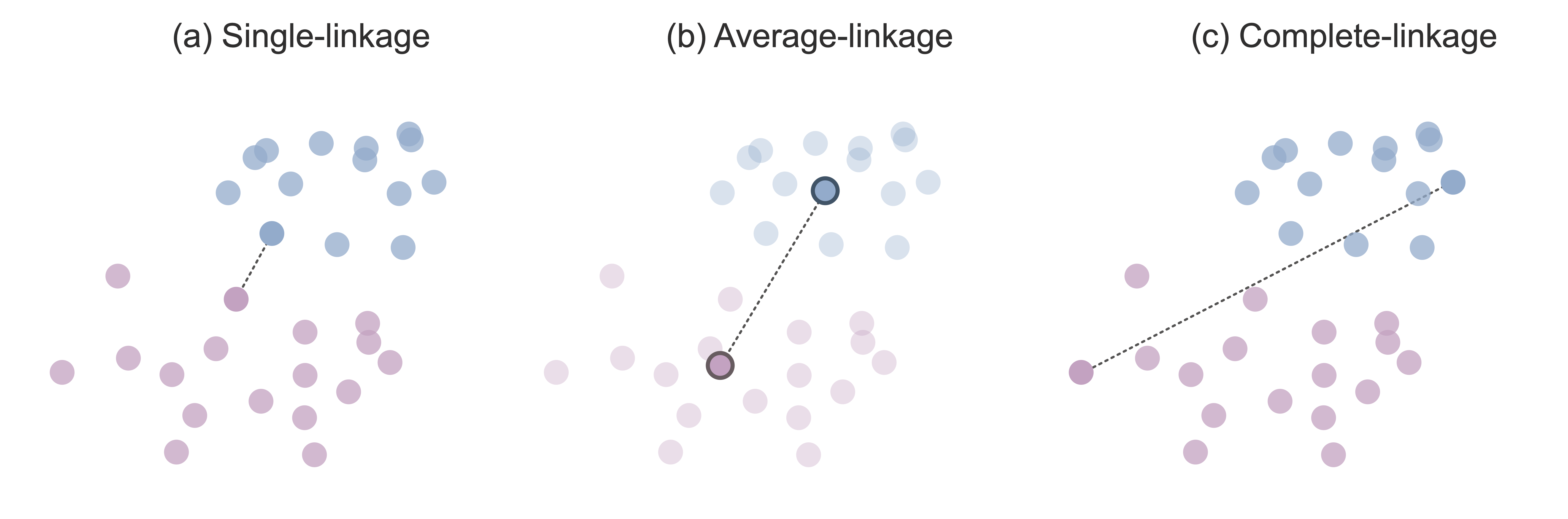
One simple definition of cluster similarity is based on the similarity between the two most similar points from each cluster. According to this definition, if there is a data point in one cluster that is very similar (e.g., in terms of Euclidean distance) to a data point in the other cluster, then these two clusters are deemed to be similar. Single-linkage hierarchical clustering refers to this version of hierarchical clustering that iteratively merges the two clusters with the two single closest data points. Figure 7.5(a) shows the single-linkage intercluster distance between two clusters.
Since it feels fairly limited to base the definition of cluster similarity solely on the single most similar pair of data points from each cluster, an alternative intercluster similarity measure defines cluster similarity as the similarity between the cluster centers of each cluster. The cluster center is defined as the average data point in the cluster (i.e., the hypothetical data point whose measurements for each variable are computed based on the average value across all the data points in the cluster). Average-linkage hierarchical clustering refers to a version of hierarchical clustering that iteratively merges the two clusters whose cluster centers are most similar to one another. Figure 7.5(b) shows the average-linkage intercluster distance between two clusters.
Another common option is to define the intercluster distance using the two most dissimilar points (e.g., the two most distant points in terms of Euclidean distance) in each cluster. This might seem a bit counter-intuitive at first. Why would we want to compute cluster similarity based on the points in each cluster that are the least similar? The idea is that if the least similar data points from each cluster are still fairly similar to one another, then all the other data points in each cluster must be similar to one another too! Complete-linkage hierarchical clustering refers to a version of hierarchical clustering that iteratively merges the two clusters whose two most dissimilar points are the most similar. Figure 7.5(c) shows the complete-linkage intercluster distance between two clusters.
One final type of linkage is Ward’s linkage. Ward’s linkage is a bit different from the others, but it also happens to be the linkage definition that yields the most meaningful hierarchical clusters for our nutrition project. Ward’s linkage hierarchical clustering involves merging the two clusters whose merger will minimize the total within-cluster variance, which is defined as the sum of the variances of the data points within each cluster. The goal is to merge the two clusters for which the resulting set of clusters will be the “tightest” (i.e., the least variable). We will discuss the within-cluster variance (or within-cluster “sum of squares”) as a cluster quality measure in more detail in Section 7.5.1.
With so many linkage options for hierarchical clustering, how do you decide which one to use? If you are conducting clustering as an exploratory technique, you may want to investigate several different clustering options. If, however, your project requires that you choose one result (e.g., you want to use the clusters to organize the foods in your app), then you can choose the one that yields the highest-quality clusters or the most meaningful clusters (determined by domain knowledge), as we will discuss in Section 7.7.1.
7.2.2 A Demonstration of Single-Linkage Clustering
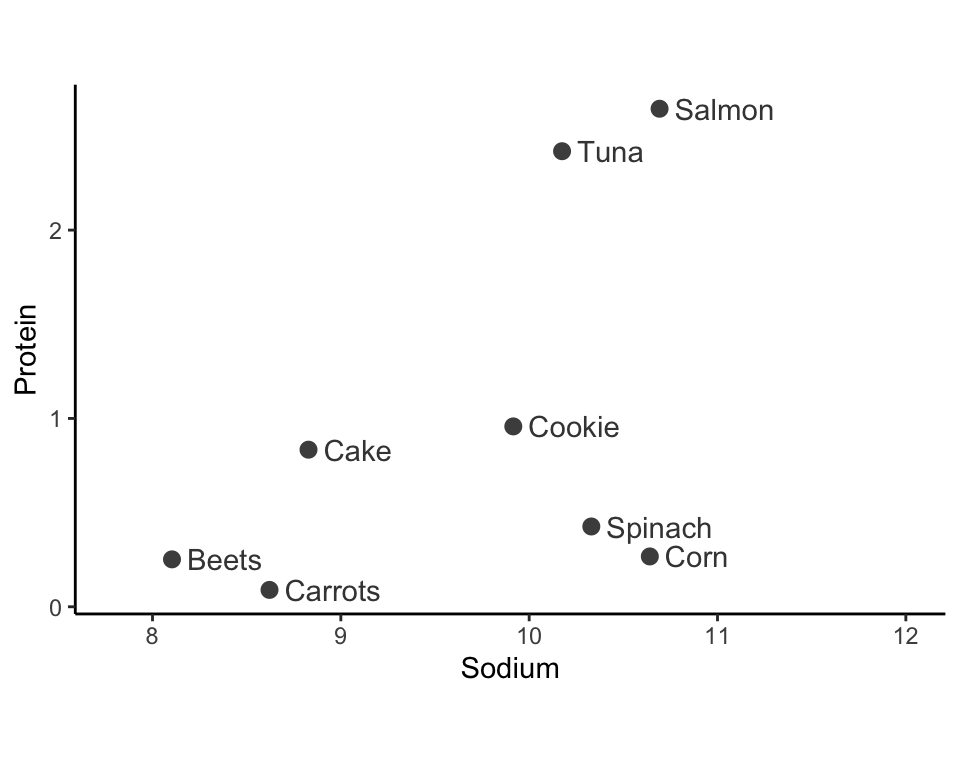
Let’s walk through a small example of using single-linkage hierarchical clustering to cluster eight food items in the two-dimensional space based on the SD-scaled “sodium” and “protein” nutrients (Figure 7.6). As an exercise, try to manually apply the other linkage methods to this example.
To perform single-linkage hierarchical clustering:
Start by placing every point in a separate cluster. In Figure 7.6, we use gray to indicate a point that is alone in its cluster (although it would technically be more accurate to give each point its own unique cluster color).
Iteration 1: Identify the two clusters that are most similar to one another based on your desired similarity measure (e.g., using the single-linkage with Euclidean distance). Merge these two clusters (by giving each data point in the two clusters the same cluster label). In Figure 7.7(a), we merge the clusters that contain the two most similar data points: spinach and corn.
Iteration 2: Find the second most similar pair of clusters, and merge them too. In Figure 7.7(b), this step merges the clusters of the beets and carrots data points.
Subsequent iterations: Continue iteratively merging the next most similar pairs of clusters until all the observations are in the same cluster. Figure 7.8 shows iterations 3–7.
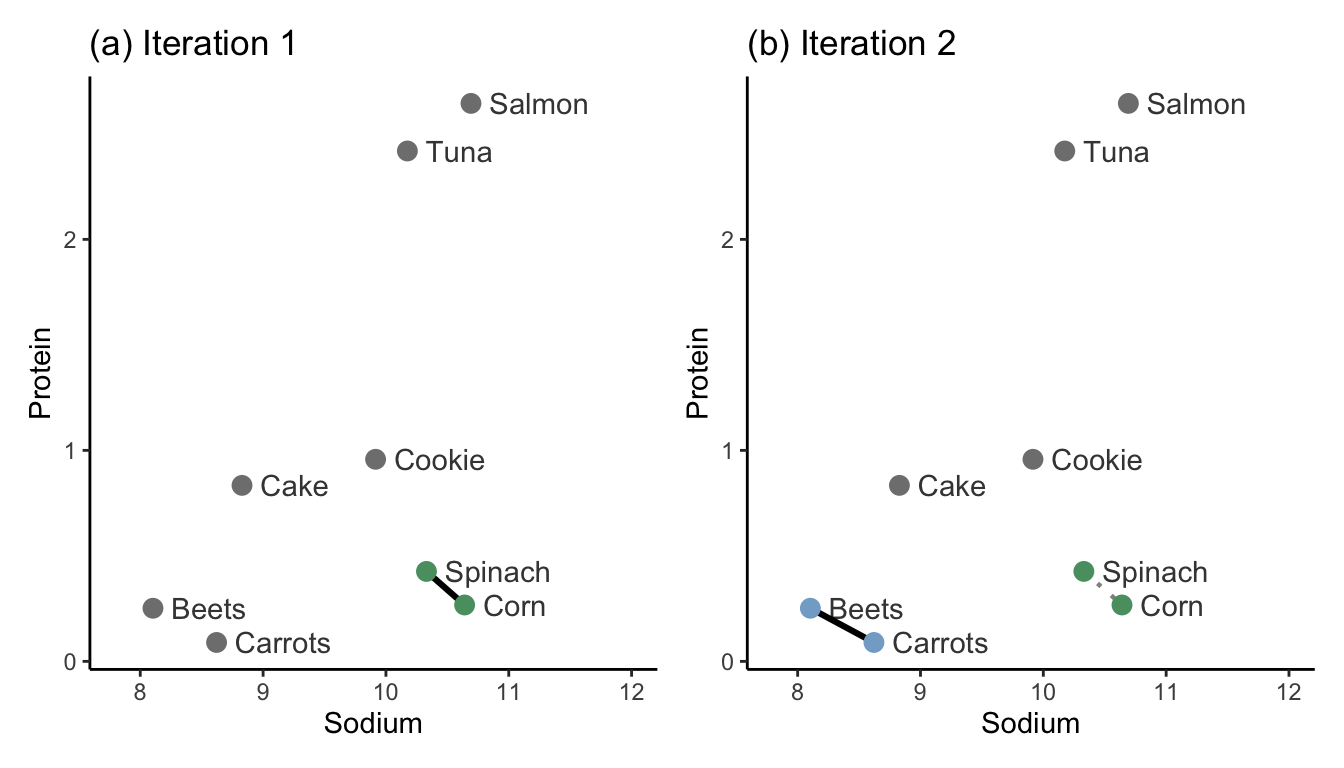

Notice how the lengths of the cluster similarity links get longer and longer with each iteration of the hierarchical clustering algorithm.
Since the algorithm starts with all points in separate clusters and ends with all the data points in the same cluster, the hope is that somewhere along the way, some interesting intermediate sets of clusters emerge. To help identify some interesting intermediate clusters we can generate a hierarchical clustering dendrogram, as shown in Figure 7.9. A dendrogram is a visual representation of the sequence of cluster merges (linkages). The height of the splits in the dendrogram corresponds to the order in which the clusters were merged: splits closer to the bottom of the dendrogram correspond to cluster merges that occurred in earlier iterations of the algorithm. For instance:
The first cluster merge was between spinach and corn.
The second cluster merge was between beets and carrots.
The third cluster merge was between salmon and tuna.
The fourth cluster merge was between the spinach/corn cluster and cookie.
The fifth cluster merge was between cake and the beets/carrots cluster.
The sixth cluster merge was between the cookie/spinach/corn cluster and the cake/carrots/beets cluster.
The seventh cluster merge was between the salmon/tuna cluster and the cluster containing all the other food items.
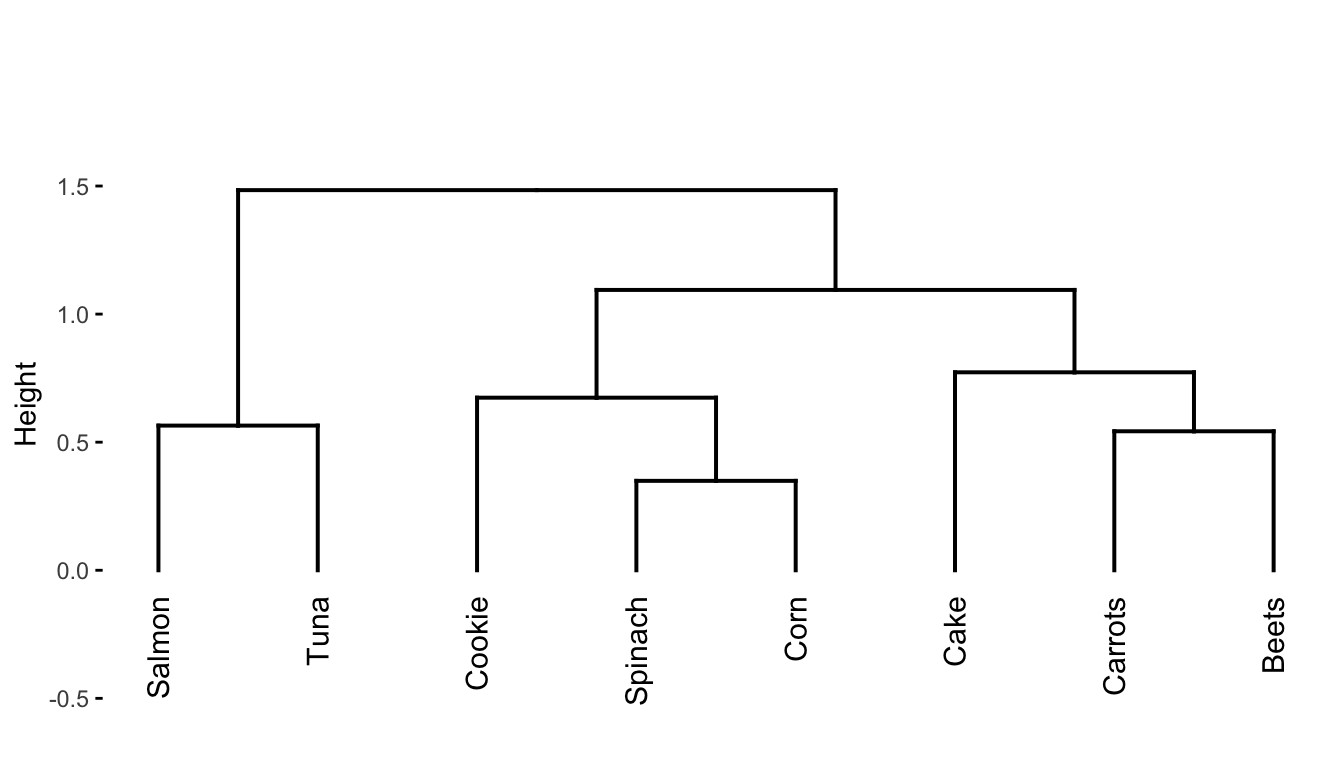
The dendrogram itself is a very useful tool for understanding the relationships between the different food items since foods that appear close together in the dendrogram are considered to be more similar to one another. To explicitly generate a set of \(K\) clusters, you can “sever” the dendrogram at a specified height, and define the set of clusters based on the separation of the observations below this height. For instance, if we sever the dendrogram at a height of around 0.95, we get the three clusters highlighted in Figure 7.10. Can you identify where to sever the dendrogram to generate a set of \(K = 2\) clusters? What are the two clusters that result? What about \(K = 4\)?

The output of a clustering algorithm is a cluster membership vector, which contains an entry for each data point denoting which cluster it is a member of. The cluster membership vector generated by the single-linkage hierarchical clustering algorithm where we split the eight food items into \(K = 3\) clusters as in Figure 7.10 is shown in Table 7.2.
| Food | Cluster |
|---|---|
| Salmon | 1 |
| Tuna | 1 |
| Cake | 2 |
| Carrots | 2 |
| Beets | 2 |
| Cookie | 3 |
| Spinach | 3 |
| Corn | 3 |
Note that you do not need to do these iterative hierarchical clustering computations yourself. There exists a built-in hclust() function in R (and a cluster.AgglomerativeClustering() class from the scikit-learn library in Python) that will do them for you.
7.3 K-Means Clustering
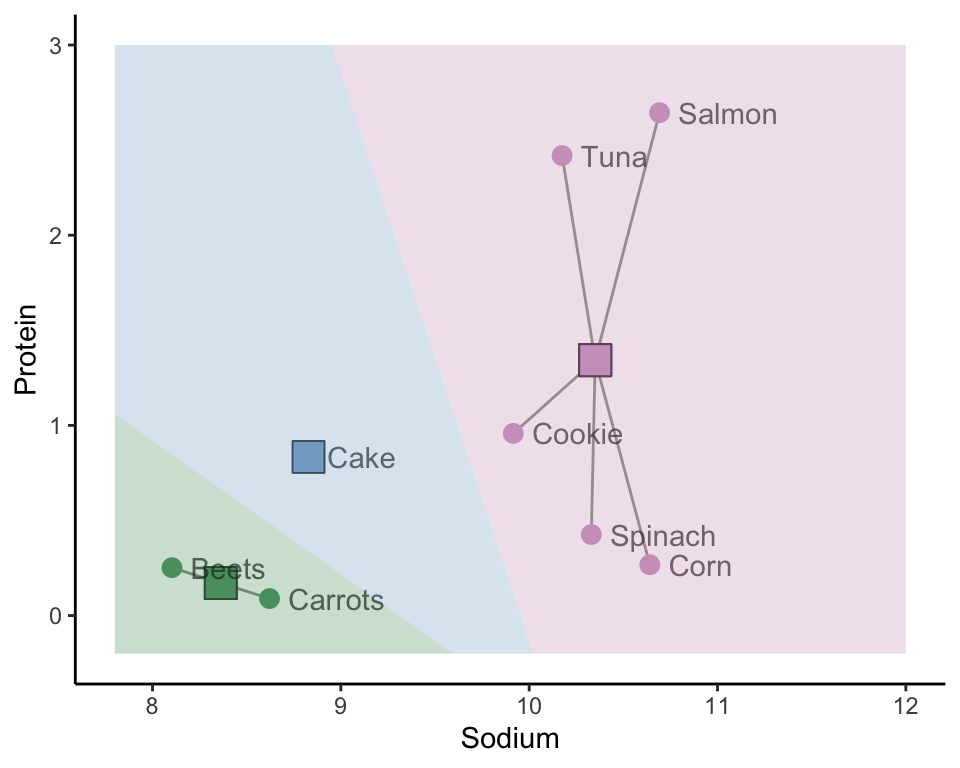
The hierarchical clustering approach is one way of clustering observations, but it is certainly not the only way. Another approach, called K-means clustering (or the Lloyd-Max algorithm in signal processing), starts by placing \(K\) random “imaginary” data points in the data space to act as random initial cluster centers (where \(K\) is the total number of clusters you want to create). These initial cluster centers may appear anywhere within the range of the data. The blue, green, and pink squares in Figure 7.11(a) represent three such randomly placed initial cluster centers (i.e., when \(K = 3\)).
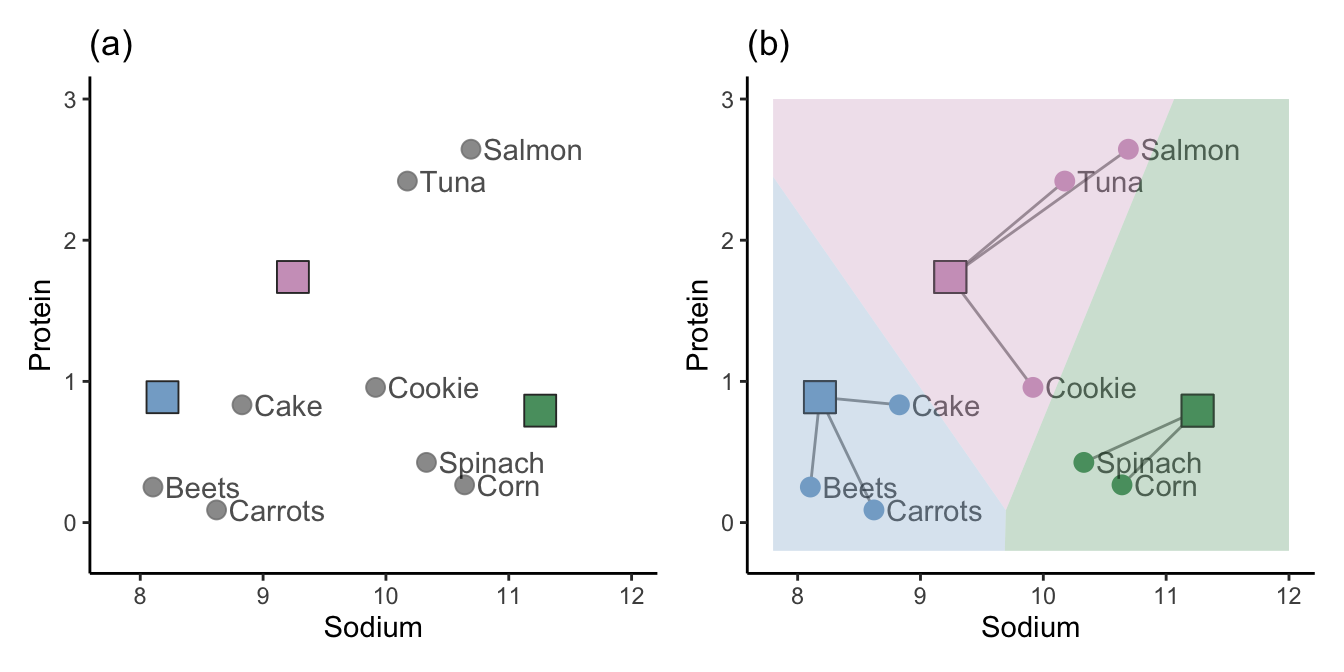
The next step is to assign the initial cluster membership of the data points based on which of the initial cluster centers they are most similar to. We will use the Euclidean distance to define similarity for this example. Figure 7.11(b) shows the initial cluster membership for each of our eight food items based on the three random initial cluster centers, where we use color and line segments to indicate which cluster the data points are placed in. The background of Figure 7.11(b) is colored based on the cluster membership that a corresponding data point in each location would have.
Do you sense a potential stability issue with this algorithm? These clusters are clearly highly dependent on the random location of the initial cluster centers. Different initial cluster centers are likely to result in very different clusters! Perhaps we can improve upon the stability of this algorithm by taking these results and refining them somehow. This is exactly what the K-means algorithm does (the process that we’ve outlined so far corresponds to just the first step of the K-means algorithm).
After defining these initial random clusters, the K-means algorithm then updates the cluster centers to be the actual center of each cluster (i.e., the average data point whose measurements for each variable correspond to the average value across all data points in the cluster), and then reassigns the cluster membership of each data point using the new cluster centers, iterating this process until the cluster membership is no longer changing. To perform K-means clustering to create \(K\) clusters:
Randomly place \(K\) initial cluster centers within the data space (Figure 7.11(a)).
Assign the cluster membership of each data point based on the initial cluster center it is most similar/closest to (Figure 7.11(b)).
Calculate new cluster centers for each cluster based on the average of all the points that were assigned to the corresponding cluster. Figure 7.12(a) shows the new (average) cluster centers, with the original random cluster centers shown as faded, transparent squares.
Redefine the cluster membership of each point based on the new cluster centers. Figure 7.12(b) shows the new cluster membership, where only one point (“Cookie”) has changed clusters based on the new cluster centers.
Repeat steps 3 and 4 until the clusters stop changing (i.e., until the algorithm has converged).
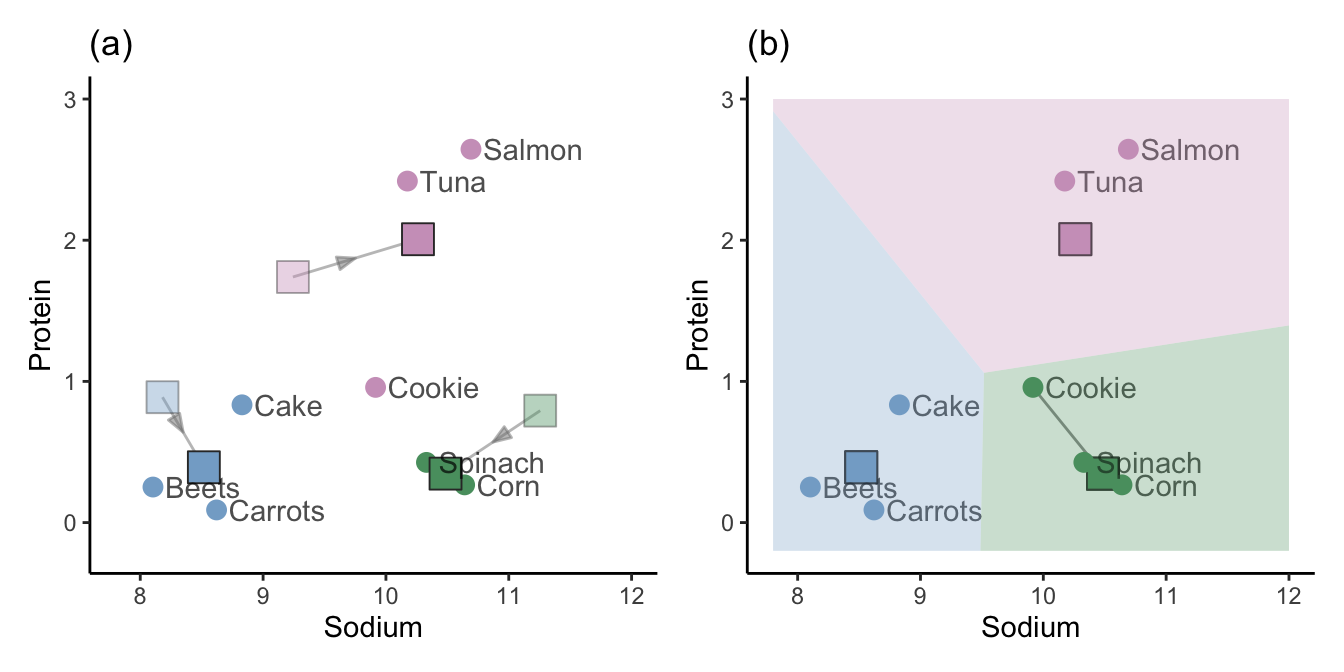
When the cluster memberships are no longer changing from one iteration to the next, we say that the algorithm has converged. The converged cluster membership vector for the implementation of the K-means algorithm using \(K = 3\) for the small example given here is the same as the hierarchical clustering membership vector from Table 7.2.
Unfortunately, there is no guarantee that the K-means algorithm will converge on the same set of clusters every time. Even after iteratively updating the cluster centers, the final results will still be dependent on the random placement of the initial cluster centers. For instance, Figure 7.13 shows an alternative set of clusters based on different initial start points. For an interesting short discussion of several related challenges in clustering problems, see Ben-David (2018).
7.3.1 The K-Means Objective Function
The mathematical objective of the K-means algorithm is to find the set of cluster centers such that the total distance from each data point to its cluster center is as small as possible.
Let’s write this using the type of mathematical notation you might encounter in the clustering literature. Our goal is to find the set of \(K\) clusters (where the \(k\)th cluster is denoted as \(C_k\), where \(k\) ranges from \(1\) to \(K\)) of the data points such that the distance, \(d(x_i, c_k)\), between each point \(x_i\) in cluster \(C_k\), and the corresponding cluster center \(c_k\) of cluster \(C_k\) is as small as possible. The loss function is the mathematical expression describing the quantity that we want to minimize to achieve this goal, which in this case can be written as
\[ \sum_{k = 1}^K \sum_{i \in C_k} d(x_{i}, c_k), \tag{7.3}\]
where \(d(x, y)\) is an arbitrary distance metric. The goal of K-means is thus to find the set of clusters, which we denote as \(\{C_k\}_{k = 1}^K = \{C_1, ..., C_K\}\) (which is a mathematical way of writing “the set of clusters \(C_1, C_2, ..., C_K\)”), such that the loss function is as small as possible. It is standard in the K-means algorithm to use the (squared) Euclidean distance metric so this loss function can be written as
\[ \sum_{k = 1}^K \sum_{i \in C_k} \sum_{j = 1}^p (x_{i,j} - c_{k,j})^2. \tag{7.4}\]
However, although the K-means algorithm aims to minimize this objective function, that doesn’t mean that it actually manages to minimize it every time. The K-means algorithm only ever finds an approximate solution to this loss function.
Don’t worry if this mathematical formulation of the K-means objective function seems a little scary. You don’t need to understand it to compute K-means clusters (but we present it here to give you a flavor of some of the notation that you will see in the clustering literature). In practice, there are functions in R (such as kmeans()) and Python (such as the cluster.KMeans() class from the scikit-learn library) that will do this computation for you.
7.3.2 Preprocessing: Transformation
Note that when applying these clustering algorithms to datasets with variables with skewed (i.e., asymmetric) distributions, we end up with many of the data points ending up in one or two big clusters, with the remaining clusters being very small. Thus, in practice, you will often find that you end up with more meaningful clusters if you can transform your variables to make them more symmetric using, say, a log-transformation. Recall that a log-transformation is a preprocessing featurization step.
We will therefore apply the cluster analyses that follow to the SD-scaled, log-transformed version of the FNDDS nutrition dataset that we introduced in Chapter 6. Note that since mean-centering does not change the relative distance between data points, mean-centering has no impact on the clusters that you obtain.
7.4 Visualizing Clusters in High Dimensions
So far, we have demonstrated these clustering algorithms on just eight food items with two variables (sodium and protein). What happens when we apply them to the full FNDDS food dataset, which has more than 8,500 food items and more than 50 nutrient variables? For this full dataset, instead of trying to compute just three clusters, let’s try to compute \(K = 6\) clusters (chosen based on the number of commonly accepted food groups). This will almost certainly be too few clusters, but we have to start somewhere. We will discuss how to choose a more appropriate number of clusters in Section 7.7.
When the clusters were computed using just two variables (sodium and protein), we were able to visualize the clusters in the corresponding two-dimensional scatterplot. But how should we visualize our clusters when they are computed using more than two variables? The following sections will outline a few techniques that you can use to explore the clusters you compute by (1) looking at a sample of data points from each cluster; (2) comparing the distributions of each variable across different clusters; and (3) projecting the clusters into a two-dimensional space (e.g., using two variables or principal components) and viewing them in a scatterplot.
In this section, we will focus on the six clusters that we identify using each of the hierarchical clustering (with Ward linkage) and the K-means algorithms. Code for creating and visualizing these clusters can be found in the 04_clustering.qmd (or .ipynb) file in the nutrition/dslc_documentation/ subfolder of the supplementary GitHub repository.
7.4.1 Sampling Data Points from Each Cluster
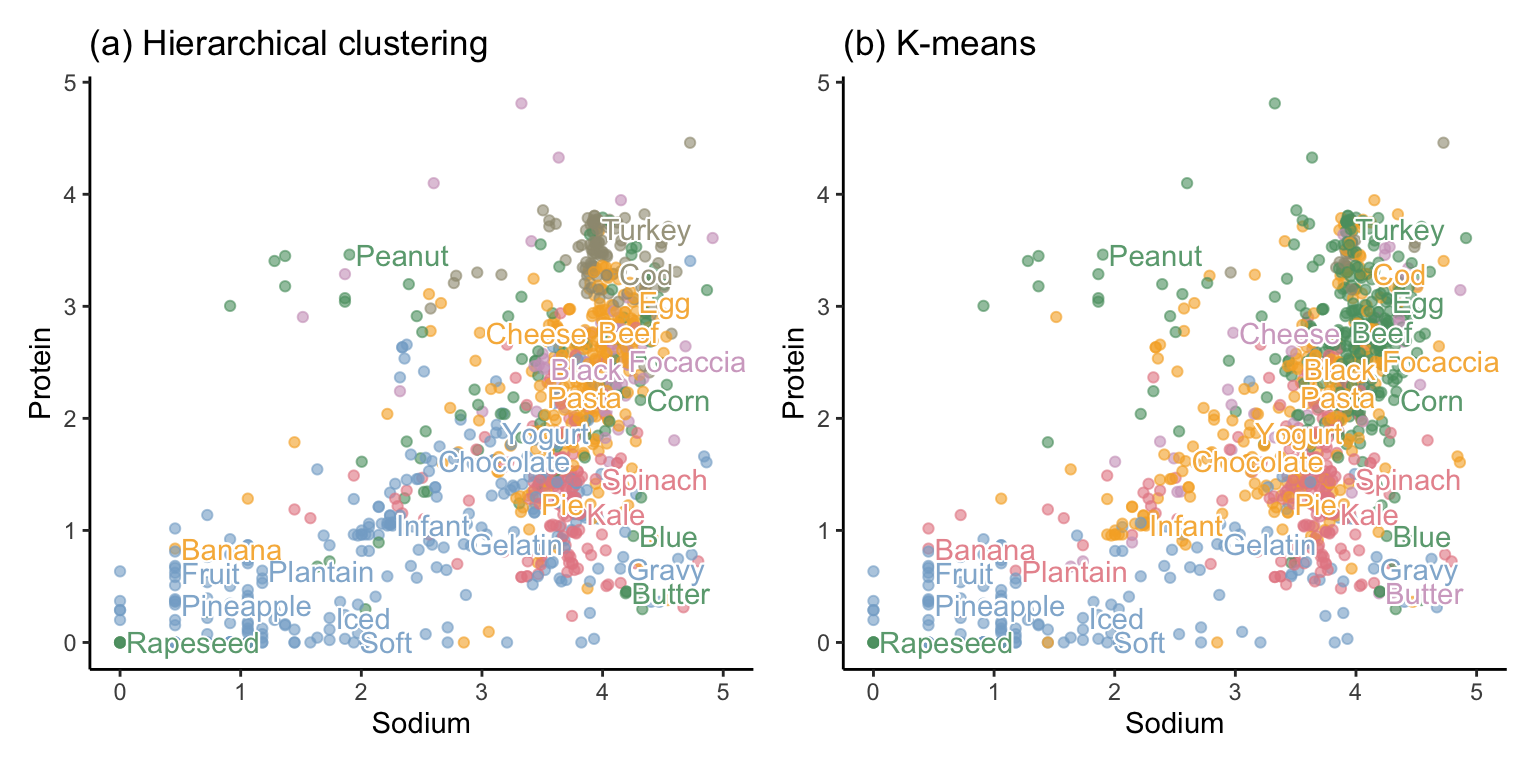
One way to visualize a set of clusters is to look at a sample of the data points (food items, in this case) that ended up in each cluster, Table 7.3 shows 15 randomly selected food items from each cluster identified using hierarchical clustering (we’re just showing the first word of each food item’s description). Based on these examples, the theme of the first cluster seems to be fruits and desserts, the second and third clusters are a bit ambiguous, the fourth cluster seems to contain cereals and beans, the fifth cluster seems to contain vegetables and chicken, and the sixth cluster seems to contain meats and seafood. That the algorithm was immediately able to separate some of the foods into themes (at least vaguely) is actually quite impressive!
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Sugar | Crepe | Grilled | Beans | Peas | Salmon |
| Peach | Egg | Potato | Bread | Chicken | Mackerel |
| Chocolate | Wrap | Almonds | Green | Tomato | Tuna |
| Applesauce | Vegetable | Cream | Bread | Artichoke | Chicken |
| Squash | Rice | Dill | Cereal | Rice | Fish |
| Beets | Chicken | Truffles | Cereal | Beans | Pork |
| Dewberries | Cookie | Cashews | Fava | Soup | Trout |
| Fruit | Breadsticks | Milk | Cereal | Peas | Frankfurter |
| Hot | Tuna | Ice | Pancakes | Tomato | Fish |
| Cactus | Lobster | Cookie | Mixed | Peas | Veal |
| Rice | Clams | Cheese | Muffin | Chicken | Beef |
| Infant | Beef | Cheese | Pretzel | Greens | Turkey |
| Chocolate | Turkey | Caramel | Beans | Peas | Pork |
| Infant | Tuna | Light | Cereal | Chicken | Frankfurter |
| Infant | Light | Cookie | Cereal | Rice | Chicken |
Table 7.4 similarly shows 15 randomly selected food items from each of the six clusters identified this time using the K-means algorithm. Notice that a few of the hierarchical and K-means cluster themes are similar: the first K-means cluster is mostly fruits and desserts, the second and third clusters are ambiguous, the fifth cluster contains vegetables (but also some meat food items), and the sixth cluster contains seafood (but less meat than the sixth hierarchical cluster). The fourth cluster, however, seems to mostly contain dairy food items and desserts.
Note that since each cluster is assigned an arbitrary number (from 1 to 6 in this example), we have manually rearranged the clusters from each algorithm so they are as comparable as possible (but this is often hard to do when the two different sets of the clusters are very different).
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Strawberries | Chicken | Veal | Cheese | Collards | Sardines |
| Jelly | Tuna | Mayonnaise | Cornmeal | Squash | Octopus |
| Energy | Chocolate | Spinach | Cheese | Spinach | Herring |
| Custard | Egg | Tortilla | Graham | Pasta | Fish |
| Jelly | Bread | Caramel | Coffee | Broccoli | Octopus |
| Fruit | Bread | Pastry | Cheese | Steak | Salmon |
| Tea | Salisbury | Cereal | Yogurt | Mustard | Salmon |
| Prunes | Corn | Frankfurter | Ice | Carrots | Roe |
| Coffee | Spanish | Seasoned | Ice | Okra | Porgy |
| Jagerbomb | Strawberry | Egg | Ice | Artichoke | Herring |
| Gelatin | Bread | Kung | Cheese | Carrots | Salmon |
| Plum | Tuna | Cheeseburger | Fudge | Cauliflower | Ray |
| Apple | Infant | Hamburger | Honey | Corn | Sardines |
| Cherries | Chocolate | Frankfurter | Coffee | Fruit | Trout |
| Soup | Infant | Beef | Cheese | Rice | Porgy |
7.4.2 Comparing Variable Distributions across Each Cluster
Another way to visualize the clusters is to visualize the distribution of the individual variables for the observations in each cluster. As an example, Figure 7.14 shows the distribution of the “carbohydrates” nutrient variable across the (a) hierarchical and (b) K-means clusters using boxplots. From Figure 7.14, the carbohydrate content of each cluster actually looks quite similar across the two algorithms.

7.4.3 Projecting Clusters onto a Two-Dimensional Scatterplot
Finally, even though our clusters were computed in a space that has many more than two dimensions, we can still visualize them in a two-dimensional scatterplot by using the cluster membership to color each data point.
Figure 7.15 shows a scatterplot of sodium and protein for 1,000 randomly selected food items (some of which we have annotated), where color is used to dictate cluster membership from each algorithm. Although the figure involves only two dimensions (corresponding to the sodium and protein nutrient variables), the color of each point is determined using the cluster memberships that were computed based on distances in the original 57-dimensional data space. However, note that once you have more than six or so clusters, it becomes hard to visualize them using color.
In this example, we have visualized the clusters using two of the original variables from the data (sodium and protein), but you could instead have chosen to visualize the clusters using, for example, two of the principal component summary variables.
7.5 Quantitative Measures of Cluster Quality
While visualizing the clusters gives us a sense of what each cluster contains, it doesn’t give us a sense of whether one set of clusters (i.e., the set of six hierarchical clusters or the set of six K-means clusters) is better or higher quality than the other. For example, does one set of clusters consist of clusters that are tighter and/or more distinct than the other?
To answer this question, we need to come up with some quantifiable performance measures for summarizing the quality of the clusters. While there are many possible cluster quality measures that you could use, the two measures that we will introduce are the Within-cluster Sum of Squares (WSS) and the silhouette score. We will also introduce the Rand Index for directly comparing two sets of clusters computed for the same collection of data points in terms of which data points are being clustered together in each set of clusters. To introduce these measures, we will return to our small sample of eight food items.
7.5.1 Within-Cluster Sum of Squares
Let’s start small by quantifying how well an individual data point is being clustered (i.e., let’s define a cluster quality score for each individual data point). From there, we can quantify the quality of an entire cluster by aggregating the cluster quality of each of the individual points.
Recall that we defined the K-means clusters based on which cluster center each point was most similar to. A natural measure of the quality of the clustering for a single data point is then how similar (close) it is to its corresponding cluster center. Recall that the cluster center3 for a specific cluster corresponds to the hypothetical average data point, whose variable measurements each correspond to the average value computed across all observations in the cluster. The corresponding quality metric computed for a cluster of observations could then be the sum of the similarity/distance between each data point and the cluster center. Extending this further, to compute this quality metric for a set of clusters you could add each of the cluster-specific aggregated distances together. The smaller this sum, the tighter the individual clusters.
While you could use any similarity/distance measure to compute this measure of cluster quality, when you use the squared Euclidean distance metric, this computation is called the Within-cluster Sum of Squares (WSS) (Box 7.8).
Figure 7.16 displays the two alternative K-means clustering results for our eight-food item example, with line segments connecting each data point to its cluster center. Each line connecting the data points to the cluster centers is annotated with the corresponding squared Euclidean distance.

Calculating the WSS involves adding up each of these individual squared distances. For our \(K = 3\) cluster example with two variables (sodium and protein), this can be written as
\[\begin{align*} WSS &=\sum_{i \in C_1} \left( \left(\textrm{sodium}_i - \overline{\textrm{sodium}}_{1}\right)^2 + \left(\textrm{protein}_i - \overline{\textrm{protein}}_{1}\right)^2\right) \\ &~~~~~~ +~ \sum_{i \in C_2} \left( \left(\textrm{sodium}_i - \overline{\textrm{sodium}}_{2}\right)^2 + \left(\textrm{protein}_i - \overline{\textrm{protein}}_{2}\right)^2\right) \\ &~~~~~~ +~ \sum_{i \in C_3} \left( \left(\textrm{sodium}_i - \overline{\textrm{sodium}}_{3}\right)^2 + \left(\textrm{protein}_i - \overline{\textrm{protein}}_{3}\right)^2\right), \end{align*}\]
where \(\sum_{i \in C_k}\) means that we are adding over the points in the \(k\)th cluster (where \(k = 1, 2,\) or \(3\)), and \(\overline{\textrm{sodium}}_{k}\) and \(\overline{\textrm{protein}}_{k}\) are the average sodium and protein values, respectively, computed for the points in the \(k\)th cluster.
A general mathematical formula for computing the WSS for a set of \(K\) clusters in a dataset with \(p\) variables is given by
\[ WSS = \sum_{k = 1}^K \sum_{i \in C_k}\sum_{j = 1}^p (x_{i,j} - c_{k,j})^2. \tag{7.5}\]
where \(x_{i,j}\) is value of the \(j\)th variable for the \(i\)th observation in the cluster and \(c_{k,j}\) is the (cluster center) average value of the \(j\)th variable across all observations in cluster \(k\). Does this formula look familiar? This is exactly the K-means loss function based on the squared Euclidean distance!
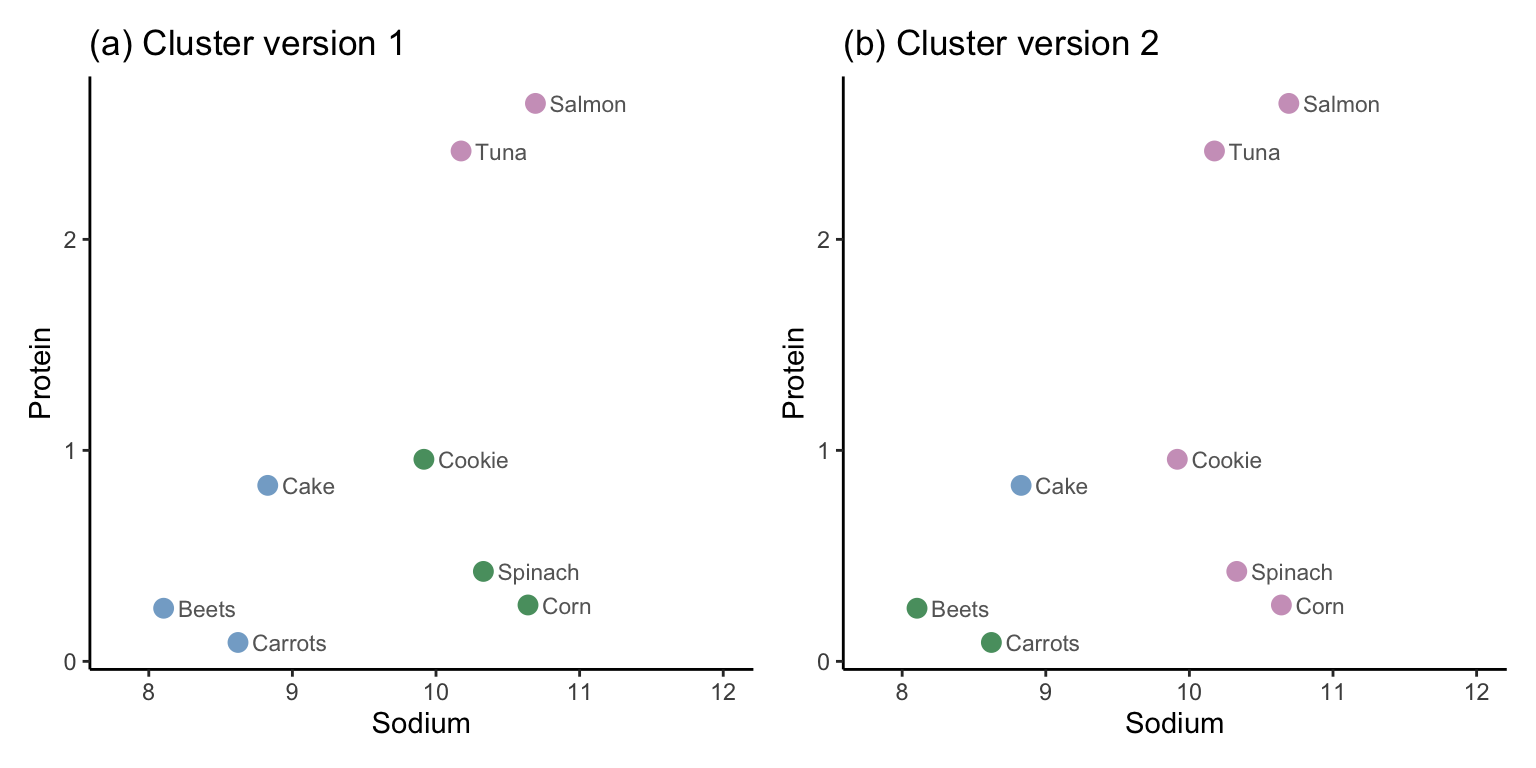
As an exercise, show that the WSS for version 1 (Figure 7.16(a)) of the clusters for the eight-data point example is equal to approximately 1.3, and for version 2 (Figure 7.16(b)), it is equal to approximately 5.5. You can do this in two ways, depending on how much work you want to do. You can start with the squared Euclidean distances annotated in Figure 7.16 (the easier option), or you can start from the SD-scaled data values shown in Table 7.5, which will involve computing the cluster centers and squared Euclidean distances yourself (the harder option). Since a lower WSS is better, this implies that the first version of the clusters is better than the second version (at least in terms of WSS, which solely provides a measure of tightness).
| Food | Sodium | Protein | Cluster (a) | Cluster (b) |
|---|---|---|---|---|
| Salmon | 10.69 | 2.64 | 2 | 1 |
| Tuna | 10.17 | 2.42 | 2 | 1 |
| Cake | 8.83 | 0.83 | 3 | 2 |
| Cookie | 9.92 | 0.96 | 1 | 1 |
| Spinach | 10.33 | 0.43 | 1 | 1 |
| Carrots | 8.62 | 0.09 | 3 | 3 |
| Beets | 8.10 | 0.25 | 3 | 3 |
| Corn | 10.64 | 0.27 | 1 | 1 |
When the clustering algorithms were each applied to the entire (SD-scaled and log-transformed) FNDDS nutrition dataset with \(K = 6\) clusters, the hierarchical clusters yielded a WSS of 335,508 and the K-means clusters yielded a WSS of 315,855. Since the K-means algorithm yielded clusters with a lower WSS, this implies that the K-means algorithm yielded tighter clusters than the hierarchical clustering algorithm. Since the objective function (i.e., the optimization goal) of the K-means algorithm was essentially designed to minimize the WSS, this is not entirely surprising.
7.5.1.1 Properties of WSS
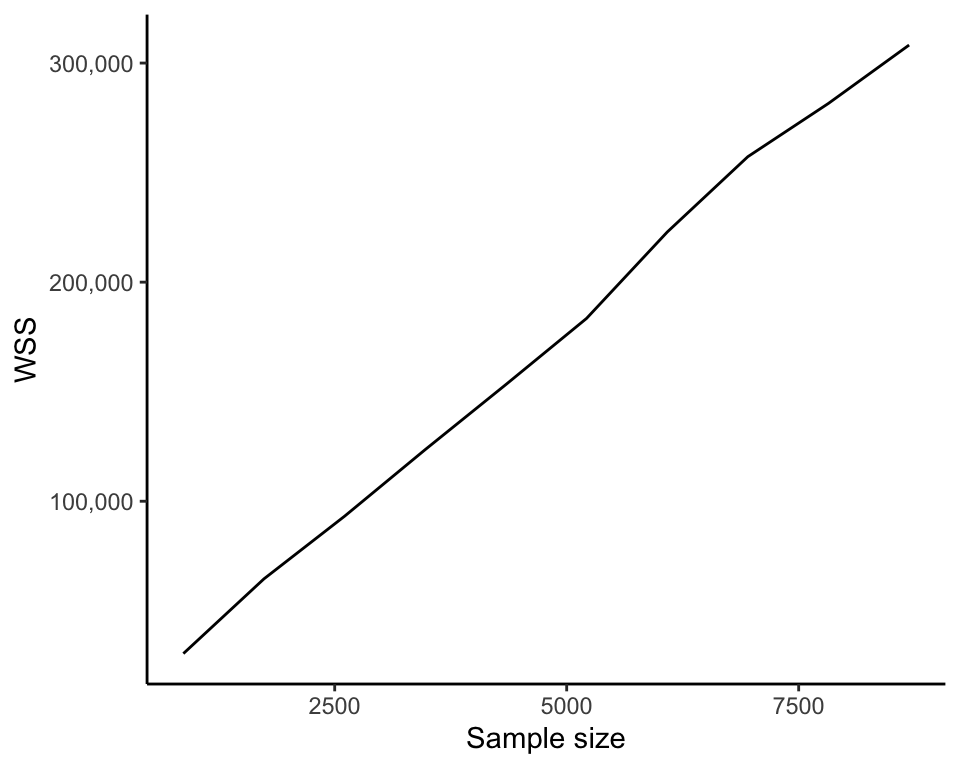
One potentially undesirable feature of the WSS that is important to note is that its value will generally become smaller as you compute more and more clusters (since the more cluster centers there are, the closer each data point will typically be to a cluster center). That is, the WSS of a set of six clusters will generally be smaller than the WSS for a set of five clusters based on the same set of data points. As an extreme example, the set of clusters in which every data point is its own cluster will have a WSS of 0. Figure 7.17 shows how the WSS decreases as we compute more and more clusters (as \(K\) increases). The upshot is that the WSS is not suitable for comparing the quality of sets of clusters that contain different numbers of clusters.

Another feature of the WSS is that, for a fixed \(K\), it will generally become larger as the number of data points increases. This is because the more data points there are, the more numbers we are adding together to compute the WSS. Figure 7.18 shows how the WSS increases when we compute six clusters on increasingly large subsamples of the FNDDS food dataset. This result would imply that the WSS is not an appropriate measure for comparing clusters computed on datasets with different numbers of observations (e.g., clusters computed using the FNDDS dataset food items and the Legacy dataset food items), but the WSS can be made comparable across datasets with different numbers of observations by scaling the WSS by the number of observations involved in its computation. Note that this comparison also requires that variables involved in the computation are on the same scale.
7.5.2 The Silhouette Score
Recall that we generally define a “good” cluster as one in which the points are similar (close) to one another (i.e., the clusters are tight), but different from the points in another cluster (i.e., the clusters are distinct). The WSS quantifies cluster tightness, but it does not take into account cluster distinctness. An alternative performance measure that takes into account both how tightly and how distinctly each data point is clustered is called the silhouette score. The idea is to create a single value that combines the following two quantities for the \(i\)th data point:
\(a_i\): The average distance between the \(i\)th data point and the other points in the same cluster as \(i\).
\(b_i\): The average distance between the \(i\)th data point and the points in the nearest adjacent cluster.
Ideally, we want \(a_i\) to be small (which means that the data point is well positioned within its cluster because it is close, on average, to all the other data points in its cluster), and \(b_i\) to be large (which means that the data point is far from the nearest adjacent cluster). In Figure 7.19, three clusters are shown using color and one blue data point is selected to be the \(i\)th data point. In this example, \(a_i\) corresponds to the average length of the two blue lines, and \(b_i\) corresponds to the average length of the three green lines.

While both \(a_i\) and \(b_i\) are informative on their own, the silhouette score (Box 7.9) combines them into a single number. How would you go about combining \(a_i\) and \(b_i\) into a single number? One option is to compute their difference, \(b_i - a_i\). A large positive difference (i.e., \(b_i\) is larger than \(a_i\)) implies that observation \(i\) is far from points in the nearest adjacent cluster and close to points in its own cluster, which is good. However, the magnitude of this difference will be heavily dependent on the scale of the variables involved in its computation. It would be nice to instead have a score that is independent of the scale of the variables in the data (e.g., a score that always lies between \(-1\) and \(1\)).
The silhouette score thus involves dividing this difference by the larger of the two values as follows:
\[ \textrm{silhouette score}_i = \frac{b_i - a_i}{\max(a_i, b_i)}. \tag{7.6}\]
A data point that has a silhouette score of approximately:
\(1\) is well clustered since it is much closer to the data points in its own cluster than it is to data points in other clusters.
\(0\) lies between clusters since it is equally close to the data points in its own cluster and in another cluster.
\(-1\) is poorly clustered since it is further from the points in its own cluster than it is to points in another cluster.
The individual data point silhouette scores can be averaged across all data points to provide a measure of the quality of a cluster or set of clusters.
7.5.2.1 The Silhouette Plot
Silhouette scores are often visualized using a silhouette plot, where the scores are plotted in descending order as horizontal bars (one for each observation) grouped by cluster. Figure 7.20 shows a silhouette plot for the two example clusters of eight food items.

The average silhouette score for the first version of the clusters for this small example is 0.63, and it is 0.19 for the second version. Remember that a higher silhouette score is better (whereas a lower WSS is better), so this implies that the first version of the clusters is better in terms of the silhouette score (this is the same conclusion that we drew when using the WSS).
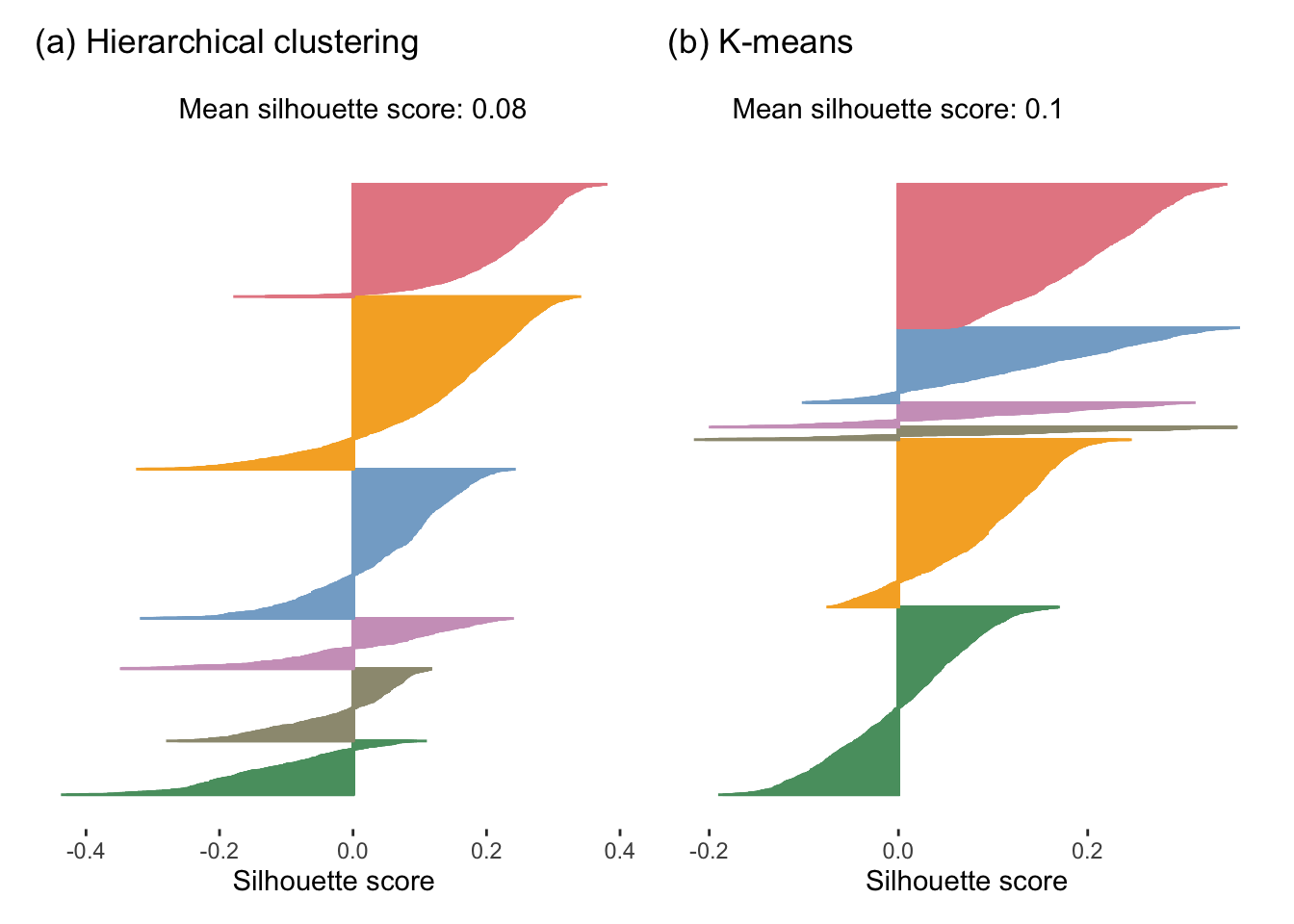
Figure 7.21 shows the silhouette plots for the hierarchical clustering and K-means algorithms applied to the full FNDDS dataset. The hierarchical clusters have an average silhouette score of 0.08 and the K-means clusters have an average silhouette score of 0.1, which implies that the K-means clusters are tighter and more distinct (i.e., “better”) than the hierarchical clusters. However, both of these average silhouette values are very far from 1, indicating that neither set of clusters is exceptionally tight and distinct overall.
Since the silhouette score is always between \(-1\) and \(1\) and does not scale with the number of clusters, you can use the silhouette score to compare sets of clusters with different numbers of clusters in them (i.e., based on different values of \(K\)).
According to both the WSS and the silhouette score, the K-means-based clusters are considered better than the hierarchical clusters. Recall that it is generally recommended to evaluate your results using multiple reasonable performance measures. If they all point toward the same conclusion, then you have strengthened the evidence underlying it.
7.6 The Rand Index for Comparing Cluster Similarity
So far, we have discussed techniques for quantifying cluster quality using measures of the tightness and distinctness of the clusters. However, the fact that two sets of clusters contain similarly tight and distinct clusters doesn’t mean that the clusters within each set are similar (i.e., in terms of which data points are being clustered together). How can we investigate whether two sets of clusters are clustering a collection of data points in a similar way?
One possible measure for comparing one set of clusters to another in terms of whether the actual data points being clustered together are similar is the Rand Index (Box 7.10). The Rand Index compares each pair of data points in terms of whether they are placed in the same cluster in both sets (versions) of clusters. A pair of data points are said to be in agreement if they are placed in the same cluster in both sets of clusters or are each in different clusters in both sets of clusters (conversely, they do not agree when the points are placed together in the same cluster in one version, and in different clusters in the other). Using this definition of agreement, the Rand Index corresponds to the proportion of data point pairs that are in agreement across the two versions of clusters:
\[ \textrm{Rand Index} = \frac{\#\textrm{pairs in agreement}}{\# \textrm{total pairs}}, \tag{7.7}\]
where “#” corresponds to the number of pairs of data points that are in agreement and “#” corresponds to the total number of pairs of data points you can create.
In R, the Rand Index can be computed using the rand.index() function from the fossil R package, and in Python, the Rand Index can be computed using the metrics.rand_score() function from the scikit-learn library.
Since it is a proportion, the Rand Index is a number between \(0\) and \(1\). The higher the Rand Index, the more similarly the two sets of clusters are clustering the data points. Note that, like the silhouette score, the Rand Index can be used to compare cluster results with different numbers of clusters.
Let’s compare the two different sets of clusters that we have computed for our small sample of eight data points, shown in Figure 7.22. To compute the Rand Index of these two sets of clusters, you first need to identify how many pairs (such as {tuna, rice} and {pretzels, potato}) of the eight data points you can create. This is a combinatorics problem, and fortunately, there exists a mathematical formula4 for how many sets of \(m\) objects you can create from \(n\) objects: \({n\choose m} = \frac{n!}{m!(n-m)!}\).
Since we are trying to compute sets of \(m = 2\) objects from a total of \(n = 8\) objects, there are \({8\choose 2} = \frac{8!}{2!6!} = 28\) possible pairs of eight data points. Next, we need to identify for how many pairs of data points the cluster memberships are in agreement across the two versions of the clusters:
The 5 pairs that are in agreement across the two sets of clusters because they are clustered together in both versions are {tuna, salmon}, {beets, carrots}, {cookie, spinach}, {cookie, corn}, and {spinach, corn}.
The 15 pairs that are in agreement across the two sets of clusters because they are in different clusters in both versions are {tuna, cake}, {tuna, beets}, {tuna, carrots}, {salmon, cake}, {salmon, beets}, {salmon, carrots}, {cake, cookie}, {cake, spinach}, {cake, corn}, {beets, cookie}, {beets, spinach}, {beets, corn}, {carrots, cookie}, {carrots, spinach}, and {carrots, corn}.
This makes a total of 20 pairs that are in agreement, which means that the Rand Index is equal to \(\frac{20}{28} = 0.71\).
When computed on the full dataset with \(K = 6\) clusters, the K-means and hierarchical clusters have a Rand Index of 0.75 (i.e., 75 percent of the pairs of food items are clustered in the same way by both clustering algorithms), which indicates that the two sets of clusters exhibit some similarity, but are certainly not identical. In exercise 24, at the end of this chapter, you will be asked to perform a simulation study to investigate how quickly the Rand Index decreases as two sets of identical clusters are artificially perturbed.
7.6.1 The Adjusted Rand Index
An alternative to the Rand Index is the adjusted Rand Index, which lies between \(-1\) and \(1\) and has been “corrected for chance.” The adjusted Rand Index is adjusted based on the index that you would “expect”5 to get if the clustering was random. An adjusted Rand Index of 1 corresponds to perfect correspondence between the two sets of clusters, and an adjusted Rand Index of \(0\) corresponds to the index for two sets of clusters for which the observations were randomly placed into their clusters (i.e., the clusters are totally meaningless). A negative adjusted Rand Index means that the clustering similarity is less than would be expected if the points were clustered randomly.
The formula for the adjusted Rand Index is a lot more complicated than the standard Rand Index
\[ \textrm{Adjusted Rand Index} = \frac{\textrm{RandIndex} - \textrm{expectedRandIndex}}{\max(\textrm{RandIndex}) - \textrm{expectedRandIndex}}. \tag{7.8}\]
When computed for two sets of clusters, \(\{C^r_k\}_{k=1}^{K_r} = \{C_1^r, ..., C_{K_r}^r\}\) and \(\{C^m_k\}_{k=1}^{K_m} = \{C_1^m, ..., C_{K_m}^m\}\), this formula becomes
\[ \textrm{Adjusted Rand Index} = \frac{\sum_{ij} {n_{ij} \choose 2} - \frac{\sum_i {n_{i\cdot} \choose 2} \sum_j {n_{\cdot j} \choose 2}}{{n \choose 2}}}{\frac12 \left(\sum_i {n_{i\cdot} \choose 2} + \sum_j {n_{\cdot j} \choose 2}\right) - \frac{\sum_i {n_{i \cdot} \choose 2} \sum_j {n_{\cdot j} \choose 2}}{{n \choose 2}}}, \tag{7.9}\]
where \(n_{ij}\) is the number of data points that are present in both cluster \(C_i^m\) and \(C_j^r\), \(n_{i\cdot}\) is the number of data points in cluster \(C_i^m\), and \(n_{\cdot j}\) is the number of data points in cluster \(C_j^r\). Fortunately, it is unlikely that you will ever need to compute the adjusted Rand Index manually because most programming languages that have an implementation of the Rand Index also have an implementation of the adjusted Rand Index (in R, one implementation of the adjusted Rand Index comes from the adjusted.rand.index() function from the fossil library; and in Python, you can use the metrics.adjusted_rand_score() function from the scikit-learn library).
When computed on the full dataset with \(K = 6\) clusters, the K-means and hierarchical clusters have an adjusted Rand Index of 0.29, which does not seem to indicate exceptional similarity, but is certainly larger than 0. In exercise 24, at the end of this chapter, you will be asked to perform a simulation study to investigate how quickly the adjusted Rand Index decreases as two sets of identical clusters are artificially perturbed. You should find that the adjusted Rand Index decreases much faster than the original Rand Index as the actual similarity between the two sets of clusters decreases.
7.7 Choosing the Number of Clusters
So far, we have only considered the results of the hierarchical and K-means clustering algorithms for \(K = 6\) clusters. But who are we to say that there are six natural groupings in the data? Might there be a better choice of \(K\) that yields more meaningful clusters?
The number of clusters, \(K\), is considered a hyperparameter of the clustering algorithms, and there are a few ways to choose its value. We generally recommend using a combination of a technique called “cross-validation” (CV) along with a healthy dose of critical thinking to choose \(K\).
7.7.1 Using Cross-Validation to Choose K
V-fold cross-validation (CV) involves creating \(V\) non-overlapping “folds” (subsets) of the original (training) dataset. If your data contains 100 observations, and you are conducting 10-fold CV, then each fold consists of 10 observations. The goal of CV is to use each fold as a pseudo-validation set, which we can use to conduct a range of predictability and stability assessments to identify a reasonable value of a hyperparameter, such as the number of clusters, \(K\). The general process of \(V\)-fold CV is summarized in Box 7.11.
Recall from our discussion of validation sets from Section 1.3.1.1 in Chapter 1, that the split into training and validation sets (and test set, where relevant) should be informed by how the results will be applied to future data (e.g., using a time-based, group-based, or random split). The same principles apply to splitting the data into CV folds.
Figure 7.23 depicts the folds in 3-fold CV. Each fold is iteratively withheld while the algorithm is trained on the remaining folds, and the trained algorithm is then evaluated using the withheld fold. This is repeated until each fold has been used to evaluate the algorithm, resulting in \(V\) different values of the relevant performance measure. After each fold has been used as a pseudo-validation set, the results across all \(V\) folds can be combined for a single CV performance evaluation.
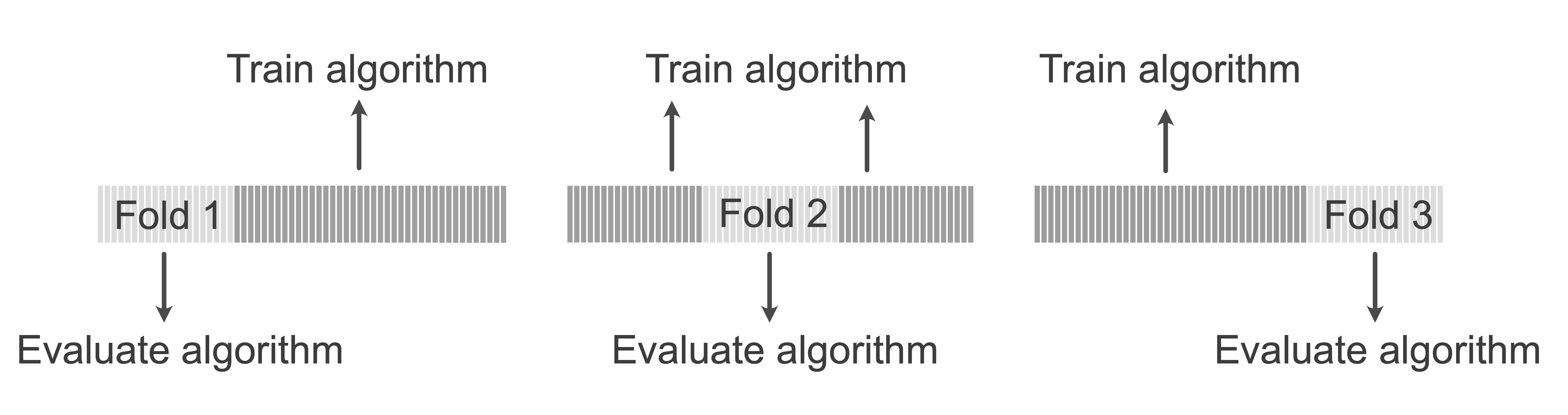
In practice, 5-fold CV (i.e., \(V = 5\)) is common for small datasets (i.e., datasets with up to a few thousand data points), and 10-fold (\(V = 10\)) CV is common for larger datasets. The extreme case where you let the number of folds, \(V\), be equal to the number of observations (i.e., each observation is its own fold) is called leave-one-out cross-validation.
Because the data used for evaluation during CV is always different from the data used to train the algorithm, CV can be used to conduct a pseudo-predictability assessment. Moreover, because each time the algorithm is trained during CV, it involves a different combination of data points, CV can also be used to conduct a pseudo-stability assessment.
Note, however, that CV evaluations are not an adequate reflection of external performance. This is because each observation that is used to evaluate the results during CV will also be used at some point to train the algorithm (this is why CV provides a pseudo-predictability assessment only). We thus recommend using CV primarily for choosing the value of a hyperparameter (such as K), rather than for providing an assessment of how your algorithm would actually perform on external/future data. Therefore, while CV provides a great lightweight PCS analysis for hyperparameter selection, we recommend that you still perform a detailed PCS evaluation of your final results.
The process of using \(V\)-fold CV to choose the number of clusters, \(K\), can be conducted as follows:
Split the data into \(V\) (e.g., \(V = 10\)) nonoverlapping “folds” (you can just do this once and use the same set of \(V\) folds for each value of \(K\)).
Remove the first fold (which will play the role of the pseudo-validation set) and use the remaining \(V-1\) folds (the pseudo-training set) to train the algorithm, which, in this case, means generating \(K\) clusters.
Evaluate the resulting \(K\) clusters using the withheld first fold (the pseudo-validation set). This can be done by clustering the observations in the withheld fold based on their proximity to each of the cluster centers for the clusters computed in the previous step. Compute the average silhouette score (or other measure of interest) for these withheld-fold clusters.
Replace the first withheld fold and remove the second fold (the second fold will now play the role of the pseudo-validation set). Use the other \(V-1\) folds to train the algorithm (i.e., generate a new set of clusters). Evaluate the clusters using the withheld second fold (e.g., using the average silhouette score).
Repeat step 4 until all \(V\) folds have been used as the withheld validation set, resulting in \(V\) measurements of the algorithm’s performance (e.g., silhouette scores).
Combine the results of the performance measures computed across all folds (e.g., by computing the average silhouette score across the folds).6
Let’s apply 10-fold CV to investigate which value of \(K\) yields the highest (and most stable) silhouette score for the K-means and hierarchical clustering algorithms. Figure 7.24 shows the distribution of the 10 silhouette scores for each CV fold for each value of \(K\) ranging from \(K = 10\) to \(K = 50\), in intervals of 5. Note that we are intentionally displaying the points (as “\(\times\)”s) over the top of the boxplots to emphasize that there are 10 values for each \(K\)—one for each withheld CV fold. The CV silhouette score (the average across all folds) for each value of \(K\) is shown as a line overlaid atop the boxplots.
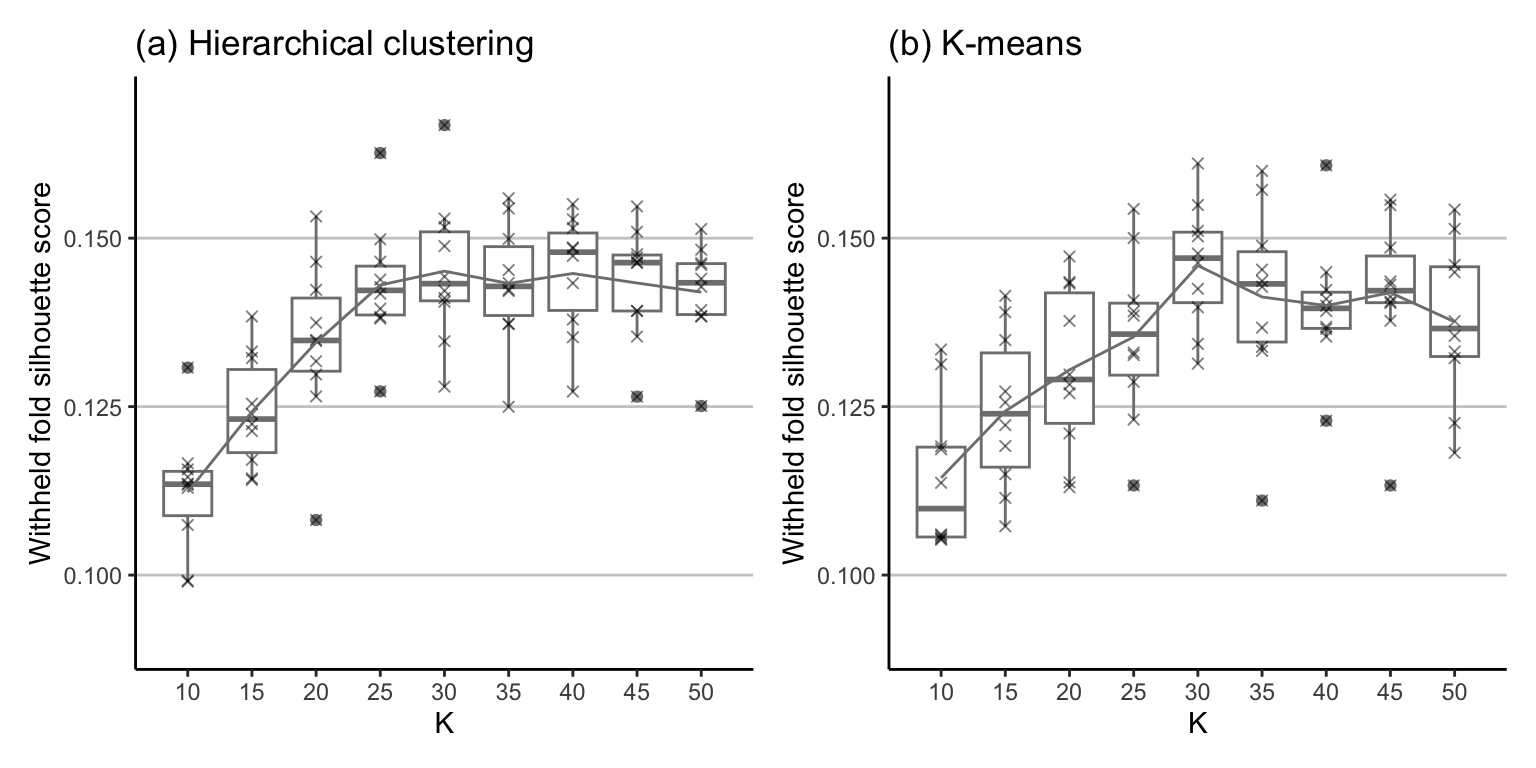
Based on Figure 7.24, is there a particular value of \(K\) that you think would be a good choice? Look at the silhouette scores themselves, as well as the stability of the silhouette scores (e.g., how much do they change across the CV folds; i.e., how spread out are the boxplots?) In general, it seems as though \(K = 30\) with the K-means clustering algorithm yields the highest CV silhouette scores across both algorithms. The average CV silhouette score when \(K = 30\) is 0.145 for the hierarchical clustering algorithm and 0.146 for the K-means algorithm.
Keep in mind that we should be using the CV results above as just one piece of evidence for what might be a good choice of \(K\) rather than as a hard rule for choosing \(K\). Let’s compute \(K=30\) clusters using the K-means algorithm and conduct some reality checks to determine if \(K = 30\) is indeed a reasonable choice. Table 7.6 shows six randomly chosen food items from the first 10 of the 30 clusters computed using the K-means algorithm, and Figure 7.25 shows the size (number of food items) of each cluster. Based on our own subjective opinion, we have provided a theme/label for each cluster.
| 1. Meats | 2. Vegetables | 3. Fish | 4. Unclear | 5. Alcohol | 6. Fats/oils | 7. Nutri-mix | 8. Infant formula | 9. Vegetables | 10. Cereal |
|---|---|---|---|---|---|---|---|---|---|
| Beef | Spaghetti | Tuna | Chow | Beer | Margarine | Whole | Infant | Beans | Cereal |
| Chicken | Mixed | Mackerel | Shrimp | Gin | Mayonnaise | Oatmeal | Infant | Turnip | Cereal |
| Bologna | Green | Herring | Fish | Beer | Coleslaw | Whey | Oatmeal | Mustard | Cereal |
| Chicken | Beef | Herring | Shrimp | Vodka | Safflower | Cereal | Infant | Beans | Cereal |
| Meat | Macaroni | Sardines | Soupy | Whiskey | Mayonnaise | Textured | Infant | Broccoli | Cereal |
| Pork | Green | Mackerel | Strudel | Long | Sandwich | Gerber | Cream | Beans | Yeast |

What do you think of these cluster results? Do they seem to be fairly sensible? The fact that we have so many clear themes emerging is quite impressive! In general, when comparing the results for other values of \(K\), we found a general trend that the higher the value of \(K\), the more specific the cluster categories are. For instance, one particular implementation of K-means with \(K = 100\) yielded highly specific categories like “pizza,” “oysters,” “corn,” “cheeseburgers,” “oatmeal,” “omelets and French toast,” and “mustard greens.”
Overall, \(K = 30\) (for the K-means algorithm) seems to perform well in terms of the quantitative CV assessments, as well as in terms of a critical thinking reality check (although you may think that a different value of \(K\) is better based on your own explorations). The code for producing these clusters (and an exploration of all 30 clusters) can be found in the 04_clustering.qmd (or .ipynb) file in the nutrition/dslc_documentation/ subfolder in the supplementary GitHub repository (feel free to play around with the code and look at a few different choices of \(K\)).
7.8 PCS Scrutinization of Cluster Results
In this section, we will conduct a PCS evaluation of the K-means cluster results with \(K=30\).
7.8.1 Predictability
Let’s evaluate the predictability of the K-means (\(K = 30\)) clusters by considering how well the foods in the external Legacy dataset get clustered when their cluster membership is determined based on which of the original 30 K-means FNDDS cluster centers it is closest to. This is similar to the CV evaluation given previously, but it uses actual external data to evaluate the clusters, rather than repeatedly using pseudo-validation data from the withheld CV folds.
First, we can compare the WSS of the original FNDDS food clusters and the Legacy food items clustered in terms of proximity to the FNDDS food cluster centers. Recall, however, that the FNDDS and Legacy datasets have different numbers of observations. This means that for the FNDDS and Legacy WSS values to be comparable, we need to divide the WSS by the number of observations used to compute it (i.e., divide the FNDDS WSS by the number of food items in the FNDDS dataset, and divide the Legacy WSS by the number of food items in the Legacy dataset). The scaled WSS for the FNDDS dataset is 19.6, and the scaled WSS for the Legacy dataset is 19.7, which are surprisingly similar to one another.
Next, we can compute the silhouette score for the FNDDS clusters and the Legacy food clusters (where the clusters are chosen using the FNDDS food cluster centers). The average silhouette score for the Legacy food items, 0.179, is actually slightly higher (i.e., better) than the silhouette score for the FNDDS foods, which was 0.142. Overall, this is a very good indication that the cluster centers that we computed for the FNDDS dataset can be used to cluster foods in other, similar datasets too (i.e., that they are predictable).
Let’s take a look at some randomly chosen Legacy food items from each cluster to see whether they match the categories that we identified for the FNDDS clusters. Table 7.7 shows six randomly selected Legacy food items from the first 10 clusters, where the cluster labels are based on the original FNDDS food themes. The FNDDS cluster labels match these Legacy food clusters surprisingly well. Overall, 25 of the 30 Legacy food clusters subjectively seem to match the corresponding FNDDS theme, which indicates that the 30 K-means cluster centers that we computed using the FNDDS dataset exhibit high predictability when used to cluster the external Legacy food dataset.
| 1. Meats | 2. Vegetables | 3. Fish | 4. Unclear | 5. Alcohol | 6. Fats/oils | 7. Nutri-mix | 8. Infant formula | 9. Vegetables | 10. Cereal |
|---|---|---|---|---|---|---|---|---|---|
| Nuts | Soup | Fish | Potsticker | Alcoholic | Oil | Babyfood | Infant | Turnip | Cereals |
| Chicken | Cornmeal | Fish | Eggs | Alcoholic | Margarine | Beverages | Infant | Parsley | Formulated |
| Pork | Tomatoes | Fish | Turnover | Alcoholic | Margarine | Beverages | Infant | Brussels | Cereals |
| Pork | Soup | Fish | Fast | Alcoholic | Oil | Protein | Headcheese | Cress | Cereals |
| Lamb | Babyfood | Fish | Muffin | Alcoholic | Oil | Cereals | Yogurt | Kale | Leavening |
| Chicken | Bananas | Fish | HOT | Alcoholic | Oil | Beverages | Infant | Spinach | Yeast |
7.8.2 Stability
Next, let’s shift our focus to investigating the various sources of uncertainty associated with our results by examining the stability of our clusters to various reasonable perturbations designed to emulate these sources of uncertainty. Specifically, we will focus on the stability of the 30 K-means FNDDS clusters to the choice of algorithm (do our results change if we use hierarchical clustering instead of K-means?), the randomness in the initialization of the K-means algorithm itself (this can be evaluated simply by rerunning the K-means algorithm), reasonable data perturbations (e.g., bootstrapping and adding random measurement noise), and the preprocessing judgment calls that we made.
Additional stability assessments that we could conduct include exploring the stability of our cluster results to the choice of similarity/distance measure (we used the Euclidean distance metric), and the stability of our clusters to alternative transformations of the data (such as square-root instead of log-transformations, or only transforming a subset of the variables), but we will leave these as an activity for the ambitious reader.
7.8.2.1 Stability to the Choice of Algorithm
Let’s compare our cluster results for \(K = 30\) when we use the K-means algorithm versus the hierarchical clustering algorithm.
When we generate 30 clusters using the hierarchical clustering algorithm (with Ward linkage) the average silhouette score (based on the FNDDS food items) is 0.113, which is only slightly less than the average silhouette score from the K-means clusters, which was 0.142. A Rand Index of 0.755 between the K-means and hierarchical clusters, however, indicates that the two sets of clusters bear some similarity to one another. (The adjusted Rand Index is equal to 0.292, indicating that there is some similarity after “adjusting for chance,” but not astonishingly high similarity.)
The clusters identified using the hierarchical clustering algorithm (with Ward linkage) also seem to contain fairly similar themes to the K-means clusters, but there is certainly not a 1-1 correspondence between the hierarchical and K-means clusters. However, note that the other linkage methods yielded much less meaningful clusters. Overall, the cluster results seem to be moderately stable to this reasonable alternative choice of clustering algorithm.
7.8.2.2 Stability to Algorithmic Randomness
Recall that the K-means algorithm starts with different random initial cluster centers every time it is run. To investigate how sensitive the eventual clusters are to these changing random initial cluster centers, we ran the K-means algorithm with \(K = 30\) four times and compared the distribution of the silhouette score using boxplots in Figure 7.26. The results are very similar across each implementation.
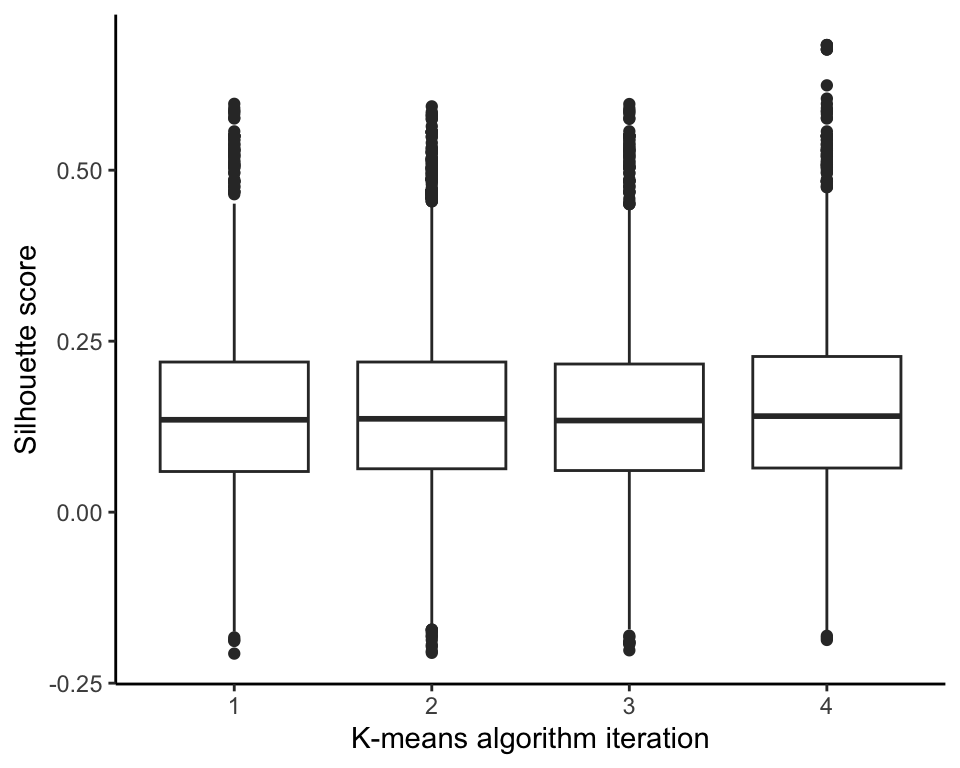
The Rand Index between the clusters generated from the original run of the K-means algorithm and the clusters generated by each of the four reruns of the algorithm are very consistent, around 0.78, but the adjusted Rand Index is a bit more variable, ranging from 0.55 to 0.65. Overall, these results indicate fairly high similarity with the original set of 30 clusters that we showed previously, but they are certainly not identical.
7.8.2.3 Stability to Data Perturbations
Next, we conduct a similar stability analysis, but this time we also perturb the data using the same perturbations that we used to conduct our principal component PCS analysis (described in Section 6.7.2.1 in Chapter 6). Specifically, we will create four perturbed versions of the data, where the perturbations each correspond to a bootstrap sample of the original dataset (to represent the fact that different food items may have been included in the observed data) and we add a small amount of random noise to the nutrient measurements (to represent possible measurement inaccuracies).
The average silhouette scores based on these data-perturbed clusters are again slightly lower than the silhouette scores for the original clusters, averaging consistently around 0.106 (the original average silhouette score was 0.142).
The Rand Index for each perturbed version of the clusters and the original set of clusters is consistently above 0.77, and the adjusted Rand Index ranges from 0.51 to 0.67, again indicating reasonable (but not perfect) similarity to the original unperturbed cluster results.
7.8.2.4 Stability to Preprocessing Judgment Call Perturbations
Finally, let’s look at how much our preprocessing judgment calls affect our results. Our clusters were based on a version of the data that has been log-transformed and SD-scaled (to ensure that nutrients with larger values do not dominate the distance algorithm), but not mean-centered (mean-centering shouldn’t affect clustering results since it doesn’t change the relative distance between the points.)
Since SD-scaling is necessary to ensure that variables with larger values do not dominate the distance calculations, we will focus on exploring how our results change when we log-transform all the variables versus none of the variables. However, it would be reasonable to also consider just transforming some of the variables (e.g., just those for which a log-transformation actively improves the symmetry of the variable’s distribution), but we will leave this exploration as an activity for the interested reader.
Figure 7.27 shows the distribution of the silhouette scores when we do and do not log-transform the nutrient variables. Note that the silhouette scores are very similar overall, but the range of silhouette scores is slightly wider (i.e., the silhouette scores are slightly less stable) when we do not transform the variables compared with when we do.

Further exploration of the clusters computed using the untransformed variables quickly reveals that they are not as “meaningful” (assessed subjectively) as the log-transformed clusters. The bar chart in Figure 7.28 shows the number of observations in each cluster when we do and do not log-transform the nutrient variables. Note that the sizes of the clusters based on the log-transformed data are much more even, whereas around half of the food items all ended up in one big cluster when they were computed using the untransformed data (which is not ideal). Moreover, looking at the food items in the clusters based on the untransformed data, we found that the two largest clusters did not have a clear theme, while the remaining clusters had similar themes to those that we found based on the log-transformed data, such as “vegetables”, “seafood”, and “cereals.”
Our clusters do not seem to be stable to our judgment call to log-transform our data. Since we get more meaningful clusters when we log-transform our data versus when we don’t, we will continue to focus on the clusters computed based on the log-transformed data.

7.9 The Final Clusters
These PCS explorations indicate that our 30 clusters are fairly predictable and moderately stable to the choice of algorithm, the K-means algorithmic randomness, and reasonable data perturbations. In showing that our results were not stable to our log-transformation judgment call, we concluded that not log-transforming the data was not a reasonable alternative judgment call. The code for this PCS analysis can be found in the 04_clustering.qmd (or .ipynb) file in the nutrition/dslc_documentation/ subfolder in the supplementary GitHub repository.
In Table 7.8, we demonstrate our first attempt to use these 30 clusters to categorize the foods in our app while also using the principal component summary nutrient variables that we created in Chapter 6 to provide some interpretable nutritional information. The cluster categories shown in Table 7.8 are far from perfect. One idea for further improving these automated cluster labels is to implement an additional layer of clustering within the “Unclear” clusters to further attempt to identify the cluster categories of these uncategorized food items. This is left as an activity for the ambitious reader.
| Food | Fats | Vitamins | Major minerals | Trace minerals | Carbs | Calories | Protein |
|---|---|---|---|---|---|---|---|
| Breads | |||||||
| Bread | low | high | high | very high | very high | very high | high |
| Desserts | |||||||
| Ice cream sandwich | high | very low | high | high | very high | high | high |
| Fruits and vegetables | |||||||
| Rice | low | low | low | low | high | low | low |
| Tomato | very low | low | very low | very low | low | very low | very low |
| Tomato with corn and okra | low | very high | low | very low | low | very low | very low |
| Tomato rice soup | very low | very low | very low | very low | low | very low | very low |
| Vegetable combination | very low | very high | low | low | high | low | low |
| Spinach | very low | very high | high | low | low | very low | low |
| Meat meals | |||||||
| Hamburger | very high | high | high | very high | high | very high | very high |
| Pizza | high | very high | high | very high | very high | high | high |
| Seafood | |||||||
| Herring | very high | high | very high | very high | very low | high | very high |
| Unclear | |||||||
| Cheese sandwich | very high | very high | high | very high | high | very high | very high |
| Turkey with gravy | low | high | high | low | high | low | high |
| Oxtail soup | high | low | very low | high | very low | low | high |
| Pancakes | high | high | very high | high | very high | very high | high |
Exercises
True or False Exercises
For each question, specify whether the answer is true or false (briefly justify your answers).
Clusters are always computed using the Euclidean distance metric.
The K-means algorithm is a randomized algorithm that may yield a different set of clusters every time it is run.
The K-means algorithm always converges to the minimizer of the K-means objective function.
The K-means clusters are always better than the hierarchical clusters in terms of average silhouette score.
One way to define a “good” cluster is by quantifying the tightness and distinctness of the cluster.
It is possible to compute the cluster centers of clusters generated from the hierarchical clustering algorithm (even though the hierarchical clustering algorithm does not itself involve computing cluster centers).
The Rand Index can be used to compare two sets of clusters only when each set contains the same number of clusters.
The Rand Index can be used to compare two sets of clusters only for the same set of data points.
The WSS can be used to compare two sets of clusters that each consist of different numbers of clusters, \(K\).
The silhouette score can be used to compare two sets of clusters that each consist of different numbers of clusters, \(K\).
Cross-validation is used widely in data science for conducting hyperparameter selection (i.e., it is not solely used for clustering problems).
Cross-validation provides a reasonable approximation to the performance of an algorithm on external data.
Conceptual Exercises
Since there are generally no “ground truth” clusters, how can you obtain evidence that a set of clusters are trustworthy? Provide at least two techniques that you might use to demonstrate the trustworthiness of a set of clusters.
Describe at least one technique that you could use to choose \(K\) (the number of clusters).
Suppose that you have a set of clusters that have been computed for a dataset that has more than two variables/dimensions.
Explain how a two-dimensional scatterplot can be used to visualize the clusters.
List two other techniques that you can use to explore the clusters.
The Rand Index is one example of a measure that quantifies the similarity between two sets of clusters. Create another measure that could be used to quantify the similarity between two sets of clusters (your measure can be much “simpler” than the Rand Index, and could just focus on the cluster centers, for example).
Identify at least three sources of uncertainty (arising at any point in the DSLC) that are associated with the cluster results obtained from the K-means clustering algorithm applied to the nutrition data. That is, identify three factors that might lead to alternative clustering results.
Mathematical Exercises
Rewrite the formula for computing WSS in Equation 7.5 instead using:
The Euclidean distance metric (rather than squared Euclidean distance).
The Manhattan distance metric.
Show that the K-means objective function (based on the squared Euclidean distance) from equation (Equation 7.4) does not change when you mean-center the data (i.e., when you replace \(x_{i,j}\) with \(x_{i,j} - \bar{x}_{j}\), where \(\bar{x}_{j} = \frac{1}{n}\sum_{i=1}^n x_{i,j}\), which is a summation over all of the observations, rather than just those within a single cluster).
The following table shows the original (unscaled) iron, sodium, and protein measurements for three food items.
Compute the Euclidean distance and the Manhattan distance between each pair of food items using all three variables. We recommend doing this manually, but you can check your results using the
dist()function in R (themethodargument of thedist()function has a “euclidean” and a “manhattan” option). In Python, you can use themetrics.pairwise.distance_metrics()function from the scikit-learn library.If the standard deviation of the iron, sodium, and protein nutrient variables are \(3.7\), \(320.0\), and \(7.9\), respectively, recompute the Euclidean distance and the Manhattan distance using the SD-scaled variables. Do the relative distances change? If so, explain why.
If these three food items all belong to the same cluster whose center is \(c = (0.8, 1.5, 0.9)\) (based on the SD-scaled variables), compute the portion of the WSS that is attributed to these three food items (i.e., add up the squared Euclidean distance from each SD-scaled food item to this cluster center).
| Food | Iron | Sodium | Protein |
|---|---|---|---|
| Frankfurter | 1.54 | 601 | 9.69 |
| Pretzels | 3.86 | 803 | 8.07 |
| Rice | 0.50 | 348 | 2.28 |
The Total Sum of Squares (TSS) corresponds to the sum of the distances between all data points and the “global” center (i.e., the average of all data points, regardless of cluster). The TSS can be written as \[TSS = \sum_{i = 1}^n\sum_{j = 1}^p (x_{i,j} - \bar{x}_j)^2,\] where \(\bar{x}_j = \frac{1}{n}\sum_{i = 1}^n x_{i,j}\) is the average/mean value for variable \(j\) across all data points.
The Between-cluster Sum of Squares (BSS) corresponds to the sum of the squared distances between each cluster center and the global center and measures how distinct the clusters are. The BSS can be written as \[BSS = \sum_{k=1}^Kn_k\sum_{j = 1}^p (c_{k,j} - \bar{x}_j)^2,\] where \(c_{k,j}\) is the \(j\)th dimension of the \(k\)th cluster center, and \(n_k\) is the number of data points in cluster \(k\).
Show that the TSS can be decomposed into the sum of the WSS and the BSS, i.e., that: \[TSS = BSS + WSS.\]
Compute the TSS, BSS, and WSS for both versions 1 and 2 of the clusters for the eight-data point example in Section 7.5.1. The SD-scaled data values are shown in Table 7.5. Confirm that \(TSS = BSS + WSS\).
Coding Exercises
At the end of the
04_clustering.qmd(or.ipynb) file in the relevantnutrition/dslc_documentation/subfolder of the supplementary GitHub repository, you will find a section labeled “[Exercise: to complete]”. In this section, write some code that applies the K-means and hierarchical clustering algorithms to cluster the nutrients/columns (rather than the food items/rows) using correlation as the similarity measure. Compare your results to the nutrient groups that we used in Chapter 6 (you can base your choice of \(K\) on these original nutrient groups). Hint: in R, both thekmeans()andhclust()R functions accept a custom distance matrix and you can convert a correlation matrix to a distance matrix (in which smaller numbers should mean “more similar”) using \(1 - |\textrm{cor}|\).Apply the hierarchical clustering and K-means algorithms (with \(K = 30\)) to cluster the food items using the principal component-transformed dataset that we computed in Chapter 6. Compare the results with the clusters computed on the original data.
The goal of this exercise is to conduct a simulation study to understand how quickly the Rand Index and the adjusted Rand Index deteriorate as we increasingly perturb a set of clusters. You can complete this exercise at the end of the
04_clustering.qmd(or.ipynb) file in thenutrition/dslc_documentation/subfolder of the supplementary GitHub repository if you wish.Use the
kmeans()function in R or thecluster.KMeans()class from the scikit-learn library in Python to cluster the (SD-scaled and log-transformed) food items into \(K = 30\) groups.Randomly perturb 5 percent of the cluster membership entries. That is, choose 5 percent of the entries of the cluster membership vector and randomly perturb them (e.g., using the
sample()function in R). For instance, if the selected entries of the membership vector were {3, 1, 3, 3, 2, 2, 4} (i.e., the first observation is in cluster 3, the second observation is in cluster 1, etc.), then one possible perturbation is {3, 3, 4, 3, 2, 1, 2}.Compute the Rand Index and the adjusted Rand Index for the new cluster membership vector and the original unperturbed cluster membership vector. R users may want to use the
rand.index()andadj.rand.index()functions from thefossilR package, and Python users may want to use themetrics.rand_score()andmetrics.adjusted_rand_score()functions from the scikit-learn library. Comment on the results.Repeat the previous steps of this exercise, this time perturbing 10, 20, and 50 percent of the data point’s cluster memberships. Comment on what you find.
Create a line plot with two lines (or two line plots, each with one line), showing (a) how the Rand Index (\(y\)-axis) changes as the proportion of data points whose cluster membership is being perturbed (\(x\)-axis) increases, and (b) how the adjusted Rand Index (\(y\)-axis) changes as the proportion of data points whose cluster membership is being perturbed (\(x\)-axis) increases.
Project Exercises
Clustering houses in Ames, Iowa The
ames_houses/data/folder in the supplementary GitHub repository contains data on the sale price and properties of each house sold in Ames, Iowa, between 2006 to 2010. This data was provided by the Ames assessor’s office and was obtained and presented by De Cock (2011). We will be using this data throughout several of the chapters in part III of this book, where our goal will be to develop a predictive algorithm for predicting the sale price of houses in Ames. For this exercise, your goal is to identify some clusters of the houses in this dataset.The
01_cleaning.qmdand02_eda.qmd(or.ipynb) files, which can be found in theames_houses/dslc_documentation/subfolder contain one example of the cleaning and exploratory data analysis (EDA) workflow for the data. Read through these files and run the code that they contain.By editing the
03_clustering.qmd(or.ipynb) file in the relevantames_houses/dslc_documentation/subfolder, conduct a cluster analysis on the housing data. Your analysis should include choosing the value of \(K\) (e.g., using CV), as well as conducting a PCS analysis of the results (assess the clusters on the withheld validation set and conduct some stability analyses to assess at least two sources of uncertainty).Summarize your clusters. What types of houses does each cluster contain?
Clustering activities using smartphone sensor data The folder in the supplementary GitHub repository called
exercises/smartphone/data/contains hundreds of measurements taken from the accelerometer and gyroscope of the smartphones of 30 volunteers (who have been split into a training and validation set) while they were conducting any of six activities (walking, walking upstairs, walking downstairs, sitting, standing, lying down). This data was collected by Anguita et al. (2013) and is hosted on the UCI Machine Learning repository.The
01_cleaning.qmd(or.ipynb) code/documentation file in the relevantexercises/smartphone/dslc_documentation/subfolder contains a template for conducting the data cleaning process for this smartphone data (we have provided some initial code for loading in the data). Clean this smartphone activity data yourself by filling in this cleaning file and write a function for cleaning and preprocessing the data (and save it in a file calledprepareActivityData.Ror.pyin theexercises/smartphone/dslc_documentation/functions/folder).Comment on how the data has been split into training and validation sets. Which splitting technique (time-based, group-based, or random) was used? Based on how the clustering results may be used in the future, do you think that the splitting technique is reasonable?
In the
02_eda.qmd(or.ipynb) code/documentation file in the relevantexercises/smartphone/dslc_documentation/subfolder, conduct an EDA of your cleaned smartphone activity dataset. Be sure to create at least one explanatory figure and conduct a PCS analysis of your results.In the
03_clustering.qmd(or.ipynb) code/documentation file in the relevantexercises/smartphone/dslc_documentation/subfolder, conduct a cluster analysis of this dataset. Specifically, you should try to identify \(K = 6\) clusters of activities without using the activity labels.Visualize your clusters. Comment on what you see. For example, do they seem to be fairly distinct?
Conduct a principal component analysis of the activity data and visualize your original clusters in the space defined by the first two principal components using a scatterplot. You may also wish to try recomputing your clusters using your principal component-transformed dataset.
Conduct a PCS analysis of your most interesting results. Specifically, assess the predictability of your clusters by assessing the clusters on the withheld validation set and conduct some stability analyses to assess at least two sources of uncertainty.
For the training data, compare the clusters that you identified with the “true” activity labels (numeric labels are contained in the
data/train/y_train.txtfile, and thedata/activity_labels.txtfile connects these numeric labels to the actual activities). Do your clusters seem to correspond to the activities?
References
If you are clustering the variables in your data (rather than the observations), you might use a correlation-based measure where two variables are considered similar if they have high correlation.↩︎
We are focusing here on distance metrics for the observations/rows of a dataset. When clustering the variables/columns of a dataset, it is more common to use similarity measures such as correlation or cosine similarity (a measure of the angle between two vectors in a data space) measure.↩︎
Although the hierarchical algorithm doesn’t involve calculating the cluster centers, you can calculate a cluster’s center by taking the average values of each variable for all the data points in the cluster.↩︎
\(n! = n \times (n-1) \times (n-2) \times... \times 2 \times 1\); for example \(4! = 4 \times 3 \times 2 \times 1\). The notation \({n\choose m}\), pronounced “n choose m”, refers to the number of sets of \(m\) objects that you can create from a total of \(n\) objects. As an example, how many pairs of objects can you create from three objects? If you enumerate these three objects as \(\{1, 2, 3\}\), then there are three possible pairs (the order of the values in the set doesn’t matter): \(\{1, 2\}\), \(\{1, 3\}\), and \(\{2, 3\}\), which can be computed by \({3\choose 2} = \frac{3!}{2! 1!} = \frac{3 \times 2 \times 1}{(2 \times 1) \times 1}=3\).↩︎
There is a technical definition of “expectation” being used here, which we won’t go into.↩︎
You can also examine the results of each individual fold to get a sense of the stability of the algorithm across the different folds.↩︎