10  Extending the Least Squares Algorithm

This is a pre-release of the Open Access web version of Veridical Data Science. A print version of this book will be published by MIT Press in late 2024. This work and associated materials are subject to a Creative Commons CC-BY-NC-ND license.

In Chapter 9, we introduced the idea of using a LS or LAD fitted line to generate response predictions based on a single predictive feature. This chapter will expand on these ideas by producing predictive linear fits that use multiple predictive features as well as regularized predictive fits with improved stability and generalizability. Note that we will primarily focus on the LS algorithm in this chapter, but many of the ideas we introduce can be similarly applied to other algorithms (such as the LAD algorithm).

10.1 Linear Fits with Multiple Predictive Features

In this book so far, we have tried to predict house prices in Ames, Iowa, using just a single feature: the living area of the house. However, it seems plausible that other measurable features of a house (such as the year that the house was built, the condition that the house is in, and the number of bedrooms) might also contain useful information for predicting sale prices. Additional predictive features can be incorporated into a linear fit by adding them to the linear combination formula. For instance, the following linear fit is designed to predict sale price based on four features: living area, quality score, the year that the house was built, and the number of bedrooms

\[\begin{equation*} \textrm{predicted price} = b_0 + b_1\textrm{area} + b_2 \textrm{quality} + b_3 \textrm{year} + b_4\textrm{bedrooms}. \end{equation*}\]

Just as in the single-predictor case, training this linear predictive fit involves finding the values of the \(b\) parameters/coefficients that minimize the loss function of your choice computed on the training data.¹ The LS squared (\(L2\)) loss function for the four-predictor linear fit is given by

\[\begin{align*} \frac{1}{n}& \sum_{i = 1}^n(\textrm{observed price}_i - \textrm{predicted price}_i)^2 \\ &= \frac{1}{n} \sum_{i = 1}^n(\textrm{observed price}_i - (b_0 + b_1\textrm{area}_i + b_2 \textrm{quality}_i \\ &~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ +b_3 \textrm{year}_i + b_4\textrm{bedrooms}_i))^2. \end{align*}\]

Just as with the single-predictor case, an explicit formula can be derived for computing the values of the \(b_j\) coefficients that minimize this squared LS loss, which is typically expressed in terms of the products (and inversions) of matrices that represent the training data (see Section 10.7). (Note that again, there is no such formula for the absolute value LAD loss.) Although it is helpful to be able to derive the coefficients using these matrix-based formulas, you don’t need to know how to do matrix computations to compute a multipredictor LS linear fit in practice, because the ls() function in R (or the linear_model.LinearRegression() class from the scikit-learn library in Python) will compute it for you. The LS fitted line with four predictor variables fit using the entire Ames housing training dataset is given by

\[ \begin{align} \textrm{predicted price} = &-871,630 + 88 ~ \textrm{area} + 19,129 ~ \textrm{quality} \nonumber\\ &~~+426~ \textrm{year} -12,667 ~ \textrm{bedrooms}. \end{align} \tag{10.1}\]

10.1.1 Interpreting the Coefficients of a Linear Fit

The first term on the right side of Equation 10.1 corresponds to \(b_0\)—the intercept term. In this example, the intercept is the “base” predicted house price (the predicted sale price of an impossible house that is \(0\) square feet, has a quality score of 0, was built in the year 0, and has 0 bedrooms). The intercept term for our four-predictor fit in Equation 10.1 equals \(-\$871,630\), which is a negative number. How should we interpret this negative intercept term? Does it mean that the algorithm is predicting that someone will pay you \(\$871,630\) to own this base impossible house? Essentially, yes. But sadly, a house that is \(0\) square feet, has a quality score of 0, was built in the year 0, and has 0 bedrooms cannot exist. Indeed, when you plug in plausible values of area, quality, year, and bedrooms, these other non-intercept terms will typically balance out the negative intercept term, and you will end up with a positive price prediction (although it is certainly still possible to get a negative price prediction for a house that has particularly small values for each variable).

Let’s take a look at the other terms in Equation 10.1:

• The coefficient of the “living area” variable (written as “area” in the equation) is \(\$88\), which implies that the predicted price increases by \(\$88\) with every square foot of living area (assuming that all other features remain the same).

• The coefficient of the “quality” variable is \(\$19,129\), which means that the predicted price increases by \(\$19,129\) with every additional quality point (assuming that all other features remain the same).

• The coefficient of the “year” variable is \(\$426/\textrm{year}\), which means that the predicted sale price increases by \(\$426\) with every additional year later that the house was built (assuming that all other features remain the same).

• The coefficient of the “bedroom” variable is \(-\$12,667/\textrm{bedroom}\), meaning that the predicted price decreases by \(\$12,667\) with every additional bedroom (assuming that all other features remain the same).

Note that these statements all concern the relationship between the predictor variables on the predicted sale price response variable, rather than the actual sale price of the houses (i.e., these are not causal statements about how the features affect the actual sale price).

The fact that the coefficient of the bedroom variable is negative is actually somewhat surprising. You’d think that a house with more bedrooms would have a higher sale price prediction, right? The coefficient of “bedrooms,” however, is the amount that the predicted price increases when an extra bedroom is added but the living area, and all other features, remain unchanged. Perhaps adding an extra bedroom does increase the predicted sale price of a house, but only when the area of the house also increases. The fact that houses with more bedrooms also tend to have a larger living area (i.e., there is a correlation between these two variables) may be causing instability in the coefficients of these two variables. Indeed, if we recompute this linear fit but we don’t include the “area” feature, we find that the bedrooms coefficient is now positive. This “area”-free fit corresponds to

\[\begin{align*} \textrm{predicted price} =& -750,097 + 37,765 ~ \textrm{quality} \nonumber\\ &~~+335~ \textrm{year} +13,935 ~ \textrm{bedrooms}. \end{align*}\]

When two variables convey similar information to one another, they are considered to be “collinear.” Since collinearity is a common cause of instability in linear fits, it is important to be wary of placing too much stock in your interpretations of coefficient values when there exist predictor variables that convey related information (see Section 10.5 for further discussion on collinearity).

10.1.2 Comparing Coefficients

What can the relative magnitude of each coefficient tell us about the predictive power of each predictor variable? Notice that in the linear fit in Equation 10.1, the “quality” score variable has a very large coefficient, equal to \(\$19,129\) per quality point, while the “area” variable has a much smaller coefficient, equal to \(\$88\) per square foot. Does the fact that the “quality” variable has a larger coefficient mean that it is more important or more predictive of sale price than the “area” variable? No, it doesn’t, and the reason is that the two variables are on very different scales. Since the quality score is always a number between 1 and 10, increasing the quality score by 1 point is a much more extreme change than increasing the living area by 1 square foot (since living area is typically on the order of thousands). The difference between a house that is 1,500 square feet and one that is 1,501 square feet is much less extreme than the difference between a house that has a quality score of 6 versus one that has a quality score of 7.

This unfortunately means that we should refrain from comparing the coefficient values to one another unless the variables are independent (that is, they are not collinear) and are either on the same scale as one another or the coefficient values themselves have been standardized (Box 10.1).

Box 10.1: Comparing Coefficients

The coefficients of different predictive features (predictor variables) are not comparable with one another unless the original features are on the same scale (either organically, or because they have been standardized) or the coefficients have been standardized.

How can we standardize a coefficient value? In general, standardizing a value involves dividing it by its standard deviation (SD). For a measurement in a dataset, the SD traditionally represents the spread of the collection of plausible values that the measurement could have taken if it were re-measured using the original (random) data collection mechanism. For a coefficient, the SD similarly represents the spread of the collection of plausible coefficient values that could have been obtained from the collection of reasonable alternative underlying datasets.

Dividing each coefficient value by its SD leads to standardized coefficient values, called “\(t\)-values,” that are comparable with one another:

\[ t_j = \frac{b_j}{SD(b_j)}. \tag{10.2}\]

Unfortunately, we can’t compute the \(t\)-values unless we can compute each coefficient’s SD, which would require that we explicitly observe all possible versions of our data (which we generally can’t). We can, however, compute an estimate of each coefficient’s SD with which we can approximately standardize the coefficients.

10.1.2.1 Estimating the SD of the Coefficients

The traditional theoretical approach of estimating a coefficient’s SD involves estimating how much the coefficient’s value varies across alternative theoretical versions of the data from a hypothetical data-generating mechanism.² These theoretical standardized coefficient \(t\)-values are often reported together with the coefficient values themselves, such as when computing the summary() of a lm() object in R.

However, rather than theorizing how our data might have looked different according to assumed theoretical properties of the data, we prefer to explicitly create plausible alternative versions of our data using perturbations, e.g., using the bootstrap perturbation technique.

Using the bootstrap to estimate the SD of a LS coefficient involves the following steps:

1. Create \(N\) (e.g., \(N = 100\) or \(N = 1,000\)) bootstrapped versions of the original dataset so that each of the \(N\) bootstrapped datasets has the same number of observations as the original data.

2. For each of the \(N\) bootstrapped datasets, compute an LS fit and extract the relevant coefficient value (so that you have \(N\) versions of each coefficient value).

3. Compute the SD of the \(N\) bootstrapped coefficients.

To empirically standardize the coefficient values using the bootstrap, we can thus divide the original coefficients (based on the original dataset), \(b_j\), by its bootstrapped SD:

\[ t_j^{\textrm{boot}} = \frac{b_j}{SD^{\textrm{boot}}(b_j)}. \tag{10.3}\]

Since the SD of a coefficient is a proxy for how stable the coefficient value is across different plausible perturbed versions of the data, a larger standardized coefficient value not only tells us that the corresponding predictive feature is an important predictor of the response, but also that the coefficient is fairly stable (i.e., because the SD is small relative to the size of the coefficient).

Table 10.1 shows the original coefficient value, the estimated SD (based on \(N = 1,000\) bootstrapped samples) for each coefficient, and the standardized coefficient (the original coefficient divided by the bootstrapped SD) for each of our four predictor variables. Despite having the smallest original (unscaled) coefficient value, the “area” variable has the largest (absolute value) standardized coefficient, followed by the “quality” score variable, indicating that these are the two variables that are most predictive of sale price. Note that since bootstrapping involves random sampling, if we repeat this assessment with a different set of bootstrapped datasets, the standardized coefficients will look slightly different (so if you coded this yourself, don’t worry if your results look slightly different from ours). The code for computing these standardized coefficients can be found in the 05_prediction_ls_adv.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the GitHub repository.

Table 10.1: The original coefficient values, the empirically estimated (bootstrapped) SD of each coefficient value, and the standardized coefficient values

Variable	Coefficient	Estimated (bootstrapped) SD	Standardized coefficient
Area	88	6	15.8
Quality	19,129	1,229	15.6
Year	426	38	11.1
Bedrooms	-12,667	2,076	-6.1

10.2 Pre-processing: One-Hot-Encoding

Notice that each of the variables in our linear fit are numeric variables. However, several of the variables in our data, such as the “neighborhood” variable, are categorical. It certainly seems plausible that houses in different neighborhoods will have different sale prices, so including neighborhood as a predictive feature in our linear fit should, in theory, help us generate more accurate sale price predictions. However, adding categorical features as a predictive variable is slightly more complicated than adding numeric ones. If you don’t think too hard about it, it might seem straightforward to just add a term for the categorical variable (such as neighborhood) into the linear fit, just as you did for the other numeric features:

\[\begin{align*} \textrm{predicted price} = b_0 + &b_1\textrm{area} + b_2 \textrm{quality} + b_3 \textrm{year} \\ &+ b_4\textrm{bedrooms} + b_5 \textrm{neighborhood}. \end{align*}\]

But this doesn’t quite make sense. To see why, imagine that you want to generate a price prediction for a three-bedroom, 1,013-square-foot house that was built in 1926, has a quality score of 6, and is located in the neighborhood of North Ames (shortened in the data to “NAmes”). Ignoring the \(b_j\) coefficients for the moment (e.g., by setting \(b_0\) to 0 and the remaining coefficients to 1), computing a sale price prediction would be akin to computing the following sum:

\[ 1013 + 6 + 1926 + 3 + \textrm{NAmes}.\]

Do you know how to add numbers and words together? We sure don’t! How then should we go about including categorical features in a linear combination-based prediction? While we could assign each neighborhood a number (e.g., North Ames is 1, Somerset is 2, and so on), this will introduce an unintended ordering to the neighborhoods based on the number that each neighborhood was assigned. Instead, the most common approach is to conduct one-hot encoding; that is, to create a binary dummy variable for each unique value, or level, of the categorical variable (Box 10.2). For any given observation, the value of each binary one-hot encoded variable that does not correspond to the observation’s categorical value (level) will equal 0, whereas the binary one-hot encoded variable that does correspond to the observation’s categorical value will equal 1.

If our categorical “neighborhood” variable has the unique values “Gilbert,” “NAmes,” “Edwards,” “BrkSide,” and “Somerset” (there are actually many more neighborhoods than this, but for demonstration purposes, we will assume that there are only these five neighborhoods), then we can include the “neighborhood” variable by including the individual neighborhood-level binary one-hot encoded variables in our linear fit as follows:

\[ \begin{align} \textrm{predicted price} = b_0 + &b_1\textrm{area} + b_2 \textrm{quality} + b_3 \textrm{year} + b_4\textrm{bedrooms} \nonumber \\ & + b_5 \textrm{Gilbert} +b_6 \textrm{NAmes} + b_7 \textrm{Edwards} \nonumber\\ &+ b_8 \textrm{BrkSide} + b_9 \textrm{Somerset}. \end{align} \tag{10.4}\]

If a three-bedroom, 1,013-square-foot house that was built in 1926 and has a quality score of 6 is located in North Ames (“NAmes”), then the values of the “Gilbert,” “Edwards,” “BrkSide,” and “Somerset” binary one-hot encoded variables for this house are all equal to 0, and the value of the “NAmes” binary one-hot encoded variable equals 1. Our simplified summation (in which all the non-intercept coefficients in Equation 10.4 equal 1) then becomes

\[ 1013 + 6 + 1926 + 3 + 0 + 1 + 0 + 0 + 0,\]

which, fortunately, we can now compute. However, recall that the interpretation of \(b_2\) (the coefficient of the quality score) in Equation 10.4 is the amount that we would expect the predicted sale price to increase if the house were given an additional quality point (keeping all other variables the same). How should you interpret the one-hot encoded neighborhood coefficients \(b_5\), \(b_6\), \(b_7\), \(b_8\), and \(b_9\) in Equation 10.4?

Extrapolating the coefficient explanations that we’ve seen so far, you might decide that \(b_5\) (the coefficient of the “Gilbert” one-hot encoded variable) corresponds to the increase in predicted sale price that is associated with the property moving to the “Gilbert” neighborhood (i.e., the predicted sale price when \(\textrm{Gilbert} = 1\), relative to \(\textrm{Gilbert} = 0\)). But what does this mean? Where was the house moved from? Wouldn’t you expect that the predicted price would increase/decrease more when moving from some neighborhoods to “Gilbert” than from others?

To address this issue, one categorical level is typically chosen to be the “reference” value. This reference binary one-hot encoded variable is removed from the linear fit so that each of the one-hot encoded variable coefficients can be interpreted as relative to the reference (which now corresponds to the neighborhood where all the remaining one-hot encoded variables are equal to 0). For instance, if the reference value of the “neighborhood” one-hot encoded variables is chosen to be “Somerset,” then the “Somerset” one-hot encoded variable is removed from the linear fit, and a house that is located in “Somerset” will correspond to all remaining “neighborhood” one-hot encoded variables being equal to 0. As a result, the coefficient of “Gilbert” can be interpreted as the amount that the predicted price would be expected to increase/decrease if the house were moved from “Somerset” to “Gilbert.”

Box 10.2: One-Hot Encoded (Dummy) Variables

Since categorical variables do not have numeric measurements, they cannot be included directly in linear combination-based predictions that require numeric predictor variables. Categorical variables can be converted to numeric variables by creating one-hot encoded/dummy variables, which correspond to a series of binary variables created for each level (i.e., each unique value) of the categorical variable.

For each observation, the value of each of the binary one-hot encoded variables is 0, except for the binary variable that corresponds to the original observed level of the categorical variable, whose value will equal 1. To avoid issues of collinearity and to aid interpretation, it is common practice to remove one of the categorical levels from a linear predictive fit to act as the reference level.

The LS linear fit with these one-hot encoded “neighborhood” variables³ (using “Somerset” as the reference neighborhood) is given by

\[\begin{align*} \textrm{predicted price} = -244,095 &+ 59~\textrm{area} + 13,862~ \textrm{quality} + 136~ \textrm{year} \\ &-2,608~\textrm{bedrooms} -17,135~ \textrm{Gilbert}\\ & -18,283~ \textrm{NAmes} -27,922~\textrm{Edwards} \\ & -28,739~ \textrm{BrkSide}. \end{align*}\]

Since all the neighborhood one-hot encoded variables have a negative coefficient, the predicted sale price must decrease when a house is moved from Somerset to any of these neighborhoods, indicating that Somerset generally has more expensive houses than the other four neighborhoods (you may want to create a visualization of the data to confirm this assumption).

10.3 Pre-processing: Variable Transformations

Recall from previous chapters that transformations (an example of featurization) that increased the symmetry of our variable’s distributions tended to improve the quality of the principal components and clusters that we computed. It turns out that transformations that improve the symmetry of our variables, such as log-transformations or square-root transformations, often lead to improved LS predictive performance too.

Box 10.3: LS and Gaussianity

While it is not required that the variables have a symmetric or Gaussian distribution to use the LS algorithm, it is sometimes the case that the algorithm will generate more accurate predictions when the predictor and response variables have a symmetric or Gaussian distribution.

However, rest assured that although the LS algorithm will often generate more accurate predictions when the underlying variables have a symmetric distribution (or have an approximately Gaussian distribution), this is not a requirement for using the LS algorithm. That said, if you find that a log-transformation of your response or any of your variables leads to a more symmetric distribution of the variable, it is worth checking to see whether this transformation will improve the predictive accuracy of your fit. We will examine the effect of applying a log-transformation to the response variable on the predictive performance of our algorithms as a part of our stability analysis in Section 10.6.2.2. Hint: applying a log-transformation to the sale price response variable greatly improves the predictive performance of our fit!

Note that log-transformations (and square-root transformations) can be used only for variables with positive values. If the variable that you are trying to transform contains negative values, you will need to pre-transform it so that all its values are positive (e.g., by adding a constant value corresponding to a quantity that is slightly larger than the smallest value in the variable).

Note also that if you train a LS fit using a transformed response variable (e.g., the log of the sale price), in order to compute a prediction of the actual response, you will need to undo the transformation that you applied. For example, if you predicted a log-transformed response, then you may want to untransform your predicted responses by exponentiating them. Similarly, if you predicted a square root-transformed response, you may want to transform your predicted responses back into their original format by squaring them.

Beyond distributional asymmetry (or a lack of Gaussianity⁴), there are a few other reasons why you may want to apply a transformation to your response and/or predictor variables when applying the LS algorithm.

10.3.1 Heteroskedasticity

Another instance in which a transformation may help improve poor predictive performance is when there is inconsistent variability in the data, known as heteroskedasticity. Figure 10.1 reproduces the plot of sale price response against living area, placing dashed lines around the general spread of the points. Notice that the points are “fanning out” slightly (i.e., there is slightly more variability in the sale price response of larger houses). This is an example of heteroskedasticity. However, since each data point in the LS loss summation is treated with equal importance, the LS algorithm typically performs best when the variability associated with each observation is relatively consistent (i.e., when there is no heteroskedasticity). Fortunately, certain transformations, such as a log-transformation of the response, can help reduce heteroskedasticity.

Figure 10.1: A scatterplot of sale price against living area, with dotted lines used to emphasize the heteroskedasticity “fanning out” effect, in which the variability of the sale price response increases with living area.

Figure 10.2 shows the log-transformed sale price response variable against the living area predictor variable. Notice how the heteroskedastic fanning out phenomenon has decreased.

Figure 10.2: A scatterplot of the logarithm of sale price against living area.

An alternative approach to applying transformations to the data to reduce heteroskedasticity is to modify the LS algorithm so it takes the heteroskedasticity into account, such as using a technique called weighted Least Squares—see Freedman (2009) or Hastie, Friedman, and Tibshirani (2001) for references.

10.3.2 Fitting Nonlinear Curves

Transformations can also be helpful when you don’t believe that the relationship between your response and a predictor variable is linear. For instance, if a quadratic curve might fit the trend of the data better than a straight line, you can use the LS algorithm to fit a quadratic to the data by transforming either the response or the relevant predictor variables, as in Figure 10.3⁵.

Figure 10.3: An LS fitted line using a quadratic transformation of total living area.

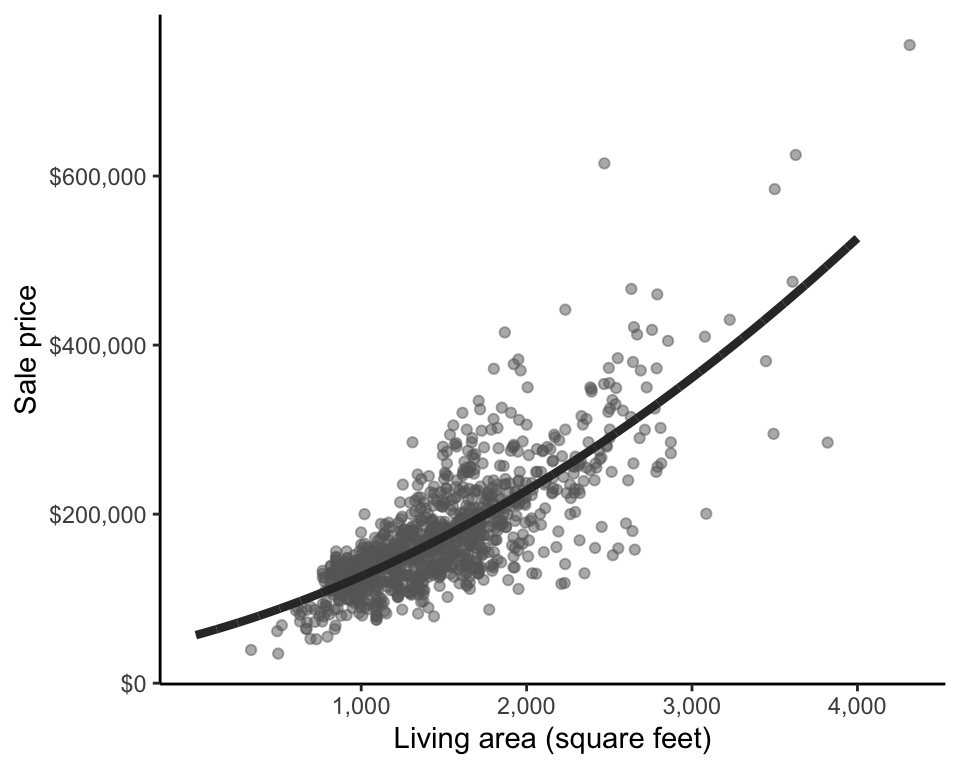
Using the LS algorithm to train a quadratic curve involves creating a new feature/variable (an example of featurization) corresponding to the squared predictor variable of interest, and adding this term to the linear fit. For instance, a quadratic fit of sale price to living area can be written

\[\textrm{predicted price} = b_0 + b_1\textrm{area} + b_2\textrm{area}^2.\]

10.4 Feature Selection

You might imagine that the more predictive features you include in your linear fit, the better your fit will be, but this is not always the case. As your fit increases in complexity (i.e., as the number of predictive features increases), the number of training data points/observations required to identify stable and generalizable coefficient values for your features increases too. Unfortunately, there is a tipping point: as the complexity of your predictive fit starts to become too great relative to the amount of training data you have, the algorithm will begin to overfit to the training data. This means that your algorithm’s increased complexity will start to capture more and more of the specific patterns that exist only in the training dataset, rather than capturing the general trends and relationships that will generalize well outside of your specific set of training data points.

How many predictive features is too many? While there are some rules of thumb, such as you should have at least 10 or 20 (or 50, depending on whom you ask) training observations for every predictive feature to avoid overfitting, there isn’t a clear answer to this question. For the default preprocessed training dataset, we have almost 50 predictive features and just over 1,100 training observations, which corresponds to about 22 training observations per predictive feature. Even if we were to include all the predictive features in our algorithm, we should be OK (at least according to the more generous rule-of-thumb).

However, once you reach the extreme end of the model complexity-data spectrum where you have fewer observations than predictor variables, the matrix-based solution to the LS algorithm actually fails.⁶ While this is unlikely to be an issue in most datasets that you will come across, there are some common types of data in which the number of features is typically substantially larger than the number of observations (such as biological gene expression data, where there are typically more gene expression measurements recorded than there are people).

The technical reason why the matrix-based solution to the LS algorithm fails in situations of extremely high-dimensional data is primarily mathematical and can be boiled down to the fact that there may be multiple possible versions of the \(b\) coefficients that minimize the squared loss function in these situations (i.e., the solution is no longer unique, which causes instability).

The simple solution when you have too many predictive features relative to the number of observations is to conduct feature selection, where you choose just a few of the most informative predictive features and discard the rest. There are many ways to decide which features to keep and which to get rid of, such as correlation screening, in which you keep only the predictive features that are most correlated with the response (based on some cutoff, whose value will be a judgment call that should be documented).

Let’s demonstrate correlation screening with an example from the Ames housing data. Recall Figure 8.3 from Chapter 8, in which we displayed the correlation of each numeric feature with sale price. The most highly correlated features (either positively or negatively) were the overall quality, greater living area, number of bathrooms, exterior quality, and kitchen quality. Overall, there are 13 features whose absolute value correlation with sale price in the preprocessed training data is equal to or above 0.5. We can thus use this correlation metric as a feature selection cutoff, keeping only the features whose correlation with the response is at least 0.5 (where this choice of cutoff was a fairly arbitrary judgment call).

One problem with this approach is that correlations aren’t designed for categorical variables (or binary variables). This technique will therefore typically be most effective for problems where both the response and predictor variables are continuous numeric variables.

However, correlation with the response is just one possible measure of feature importance you can use to determine which features to include in your fit. Some predictive algorithms, such as Random Forest (RF; see Chapter 12), come with built-in feature importance metrics that specify how important each feature is for generating the predictions, which can be used to guide feature selection. Other metrics traditionally used in statistics include the Akaike Information Criterion (AIC), and the Bayesian Information Criterion (BIC), which we won’t go into in this book (see Stoica and Selen (2004) for more information).

10.5 Regularization

An alternative way to restrict the complexity of an LS fit is to regularize the LS algorithm. Regularizing a predictive algorithm involves forcing it toward a simpler solution by adding constraints to the minimization/optimization problem, which tends to have the added effect of improving the stability of the algorithm. In this context, regularization acts as an automated algorithmic feature selection technique that we build into the algorithm when we train it.

Regularization can be used to address both problems of overfitting (when there are too many predictive features relative to the number of observations) and collinearity (when the training data contains variables that are highly correlated with one another), both of which tend to arise when there are large numbers of predictive features (i.e., the data is high-dimensional).

Recall that collinearity is a common cause of instability in LS predictive fits. To understand why, imagine that you have two variables that are both essentially measuring the living area of the house and have an extremely high correlation with one another of around 0.98. Since it doesn’t make sense to change the value of one of the area variables while keeping the value of the other area measurement constant (since they are so tightly connected), our original interpretation of the coefficients (as the amount that the predicted price would increase when the corresponding variable increases by one unit without changing the value of any of the other variables) falls apart.

Let’s do a small experiment to demonstrate this problem. We will use LS to train two versions of the following linear predictive fit based on the living area, quality score, year built, and bedroom predictor variables. The first version is our original four-predictor fit:

\[\begin{align*} \textrm{predicted price} = b_0 & ~+~ b_1 \textrm{year} ~+~ b_2\textrm{bedrooms} \nonumber\\ &+~ b_3 \textrm{quality} ~+~ b_4\textbf{area}. \end{align*}\]

The second fit will include an additional living area predictor (“area2”) that is highly correlated (with a correlation of 0.98) with the original “area” variable:

\[\begin{align*} \textrm{predicted price} = b_0 &~+~ b_1 \textrm{year} ~+~ b_2\textrm{bedrooms} \nonumber\\ &+ ~b_3 \textrm{quality} ~+~ b_4\textbf{area} ~+~ b_5\textbf{area2}. \end{align*}\]

To get a sense of the stability of the coefficient values for each of these two linear fits, we trained each fit 500 times, each time using a different bootstrapped sample of the training data. The boxplots in Figure 10.4 show the distribution of the resulting \(t\)-values (standardized coefficients using the theory-derived SD value) from the 500 versions of each of the two linear fits.

Figure 10.4: Boxplots displaying the distribution of the standardized coefficient values (a) when there is only one living area variable and (b) when there are two highly correlated living area variables.

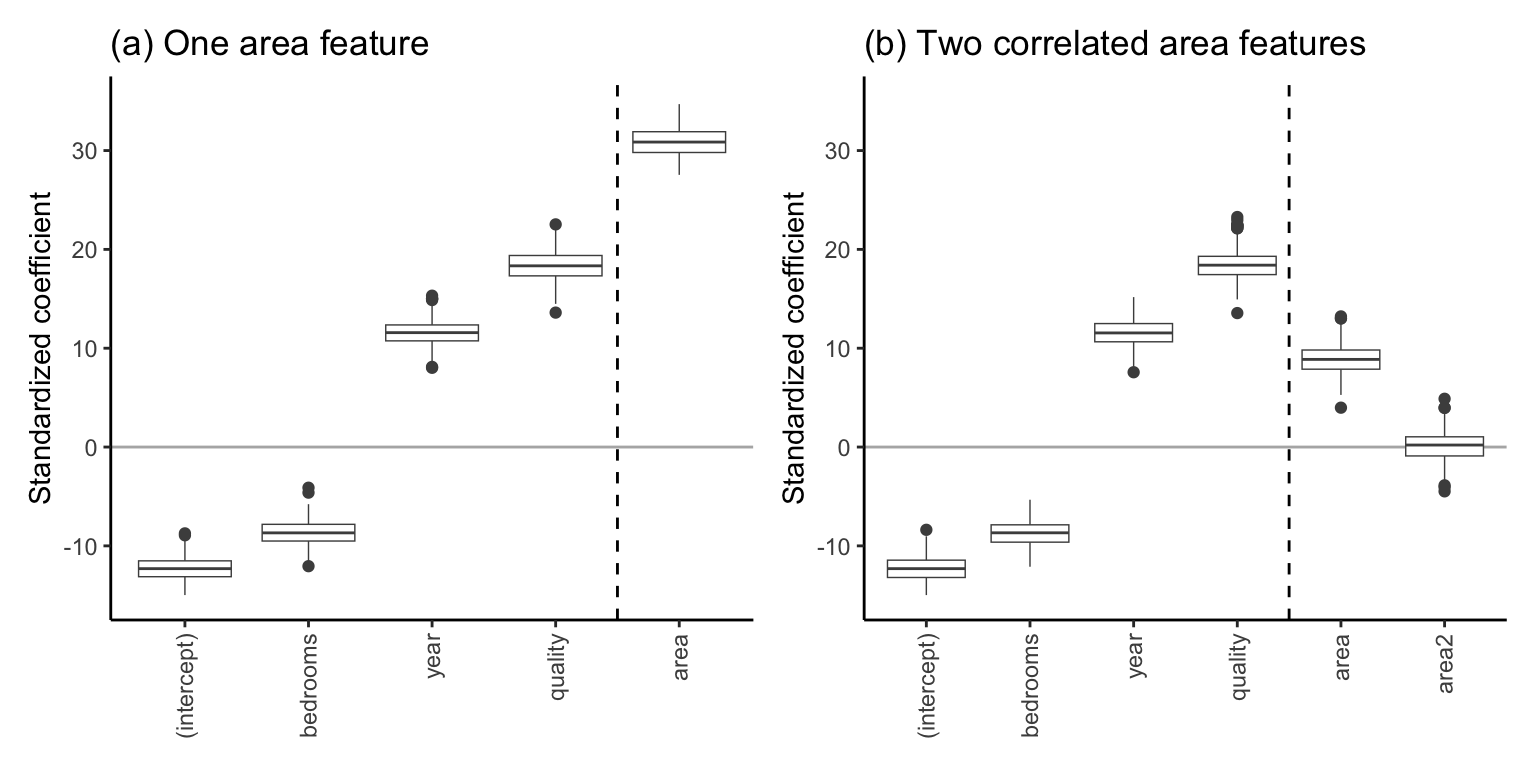
Notice that when we include the additional highly correlated living area feature (Figure 10.4(b)), the magnitude of the area coefficient decreased dramatically compared with the original version in Figure 10.4(a). This is an example of instability resulting from collinearity: the inclusion of a single highly correlated variable dramatically changed the value of the original area variable coefficient. The reason is that in the fit with two area features, the influence of the original area feature on the predicted response is now shared with the second total living area variable.

How can regularization help with instability? Let’s start by considering the format of the original unregularized LS loss. Figure 10.5 displays a three-dimensional (3D) surface in which the vertical position (height/\(z\)-axis) of the surface corresponds to the value of the LS squared loss function for a range of values of the intercept \(b_0\) and the area coefficient \(b_1\) (\(x\)- and \(y\)-axes), based on the single-predictor linear fit, \(\textrm{predicted price} = b_0 + b_1 \textrm{area}\).

Figure 10.5: A 3D surface representation of the LS loss (vertical \(z\)-axis) across different values of \(b_0\) and \(b_1\) (\(x\)- and \(y\)-axes).

The values of \(b_0\) and \(b_1\) that correspond to the LS solution are the points on the \(b_0\) and \(b_1\) axes that correspond to the lowest point of the surface (i.e., the values that minimize the loss function). Do you notice a potential problem? There is a prominent valley along which the surface minimum travels, which means that there is a range of values of \(b_0\) and \(b_1\) that seem to almost equivalently minimize the squared loss. That is, while there might technically be some values of \(b_0\) and \(b_1\) that correspond to the exact lowest point in this valley, its position is not obvious, which can lead to instability when estimating the \(b_0\) and \(b_1\) values that minimize the loss.

10.5.1 Ridge

One way that we could get around this issue (i.e., force a stable solution) is by “pulling up” the sides of this loss surface to create a clearer minimum, as in Figure 10.6. Mathematically, this involves adding a regularization constraint to the coefficients when calculating the LS solution, which means that the loss artificially increases as the values of \(b_0\) and \(b_1\) move farther from a particular point, usually chosen to be the point at which \(b_0 = 0\) and \(b_1 = 0\). Since the LS algorithm is trying to minimize the loss, this forces \(b_0\) and \(b_1\) to stay relatively close to \(b_0 = 0\) and \(b_1 = 0\).

Figure 10.6: A 3D surface representation of the ridge loss (vertical \(z\)-axis) across different values of \(b_0\) and \(b_1\) (\(x\)- and \(y\)-axes).

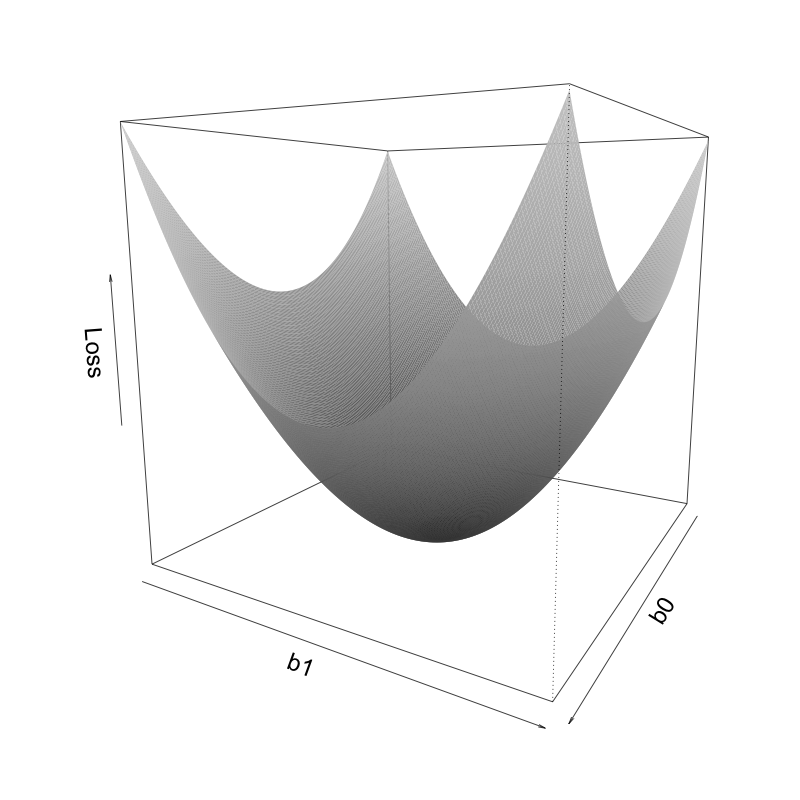
The result is that there is now a much clearer minimum along the loss surface, meaning that the values of \(b_0\) and \(b_1\) that minimize the loss will be a lot more stable (and will also be closer to zero). The technique that imposes a quadratic (squared) L2 constraint or penalty term is called L2 regularization, and, when used with the LS algorithm, it is called the ridge algorithm.

For the single-predictor LS example, the ridge regularization solution can be written as a constrained LS problem:

Find the values of \(b_0\) and \(b_1\) that make the LS loss

\[ \sum_i\left( \textrm{observed price}_i - (b_0 + b_1 \textrm{area}_i )\right)^2 \tag{10.5}\]

as small as possible, subject to \(b_0^2 + b_1^2 < t\) for some \(t \geq 0\).

This final expression, \(b_0^2 + b_1^2 < t\), is the L2 constraint (\(L2\) because the coefficients are squared), and \(t\) is called the regularization hyperparameter.⁷

The smaller the value of the hyperparameter \(t\), the more regularization you are implementing (i.e., the more you are shrinking the coefficients toward zero). The value of the regularization hyperparameter, \(t\), is something that you, the analyst, must choose, typically using cross-validation (CV; see Section 10.5.4).

Note that sometimes the ridge regularization problem is presented slightly differently as a “penalized LS” problem as follows:

Find the values of \(b_0\) and \(b_1\) that make the regularized LS loss

\[ \sum_i\left( \textrm{observed price}_i - (b_0 + b_1 \textrm{area}_i )\right)^2 + \lambda (b_0^2 + b_1^2) \tag{10.6}\]

as small as possible (for some \(\lambda \geq 0\)).

In this formulation, a penalty term is added directly to the loss function itself, which involves a different regularization hyperparameter, denoted as \(\lambda\). The \(\lambda\) hyperparameter for this penalized version of the ridge algorithm and the \(t\) hyperparameter for the constrained version of the ridge algorithm are essentially equivalent (they have a 1-1 correspondence), but they have different interpretations. For the original constrained formulation, the smaller the value of \(t\), the more regularization is being implemented, whereas for this penalty-term formulation, the larger the value of \(\lambda\), the more regularization is being implemented. Note that most software packages implement this penalized version of ridge, rather than the constrained version.

It turns out that just as there is an exact matrix-based solution for the original LS algorithm, there is also an exact matrix-based solution for the ridge algorithm (shown in Section 10.7). However, you don’t need to manually implement this algorithm yourself because the glmnet() function from the “glmnet” R package (Friedman, Hastie, and Tibshirani 2010) and the linear_model.Ridge() class from the scikit-learn Python library can do it for you.

10.5.2 Lasso

Instead of pulling up the sides of the loss surface into a quadratic curve, an alternative approach is to instead “fold” the sides up, so that the minimum is a clear single point, as in Figure 10.7. Mathematically, this approach also involves adding a penalty term to the loss, but this time the penalty term involves the sum of the absolute value coefficients (rather than the sum of the squared coefficients, as in the case of ridge regularization). The technique that imposes an absolute value L1 constraint or penalty term is called L1 regularization, and, when applied to the LS algorithm, it is called the lasso algorithm.

Figure 10.7: A 3D surface representation of the lasso loss (vertical \(z\)-axis) across different values of \(b_0\) and \(b_1\) (\(x\)- and \(y\)-axes).

For the single-predictor LS example, the constrained lasso regularization problem can be written as follows:

Find the values of \(b_0\) and \(b_1\) that make the LS loss

\[ \sum_i\left( \textrm{observed price}_i - (b_0 + b_1 \textrm{area}_i )\right)^2 \tag{10.7}\]

as small as possible, subject to \(\vert b_0\vert + \vert b_1 \vert < t\) for some \(t \geq 0\).

The alternative (but equivalent) penalized formulation of the lasso algorithm is given by:

Find the values of \(b_0\) and \(b_1\) that make the regularized LS loss

\[ \sum_i\left( \textrm{observed price}_i - (b_0 + b_1 \textrm{area}_i )\right)^2 + \lambda (|b_0| + |b_1|) \tag{10.8}\]

as small as possible (for some \(\lambda \geq 0\)).

Unlike the penalized form of the ridge algorithm, there is no closed-form solution to the lasso problem, so it must be solved using convex optimization techniques. Fortunately, you don’t need to know how to do this manually, because the glmnet() function from the “glmnet” R package (Friedman, Hastie, and Tibshirani 2010) and the linear_model.Lasso() class from the scikit-learn Python library can do it for you.

Box 10.4: Regularized Least Squares

The Least Squares (LS) algorithm can be regularized by adding a constraint or a penalty term to the loss function that forces the squared (for ridge) or absolute value (for lasso) sum of the coefficients to be less than a certain value. This encourages improved stability of the coefficients by pulling them toward zero rather than allowing them to take arbitrary values. The amount of regularization (the extent to which the coefficients are shrunk toward zero) is controlled by a regularization hyperparameter that is typically chosen using cross-validation (CV). Both lasso and ridge can be implemented using the “glmnet” R package and the scikit-learn Python library.

While L2-regularization (ridge) shrinks the coefficients toward zero (without actually yielding coefficients equal to 0), L1-regularization (lasso) will often shrink several of the coefficients all the way to 0. You can therefore use lasso as a feature selection technique by only keeping the variables whose coefficients were not shrunk completely to 0 in the L1-regularized (lasso) fit. (Note that the AIC and BIC feature selection techniques that we mentioned in Section 10.4 are special cases of L0,⁸ rather than L1 or L2, regularization.)

Finally, note that it is possible to implement both lasso (L1) and ridge (L2) regularization simultaneously, by implementing two constraints or adding two penalty terms (one for the squared sum and one for the absolute value sum of the coefficients). This algorithm is called elastic net. Lasso, ridge, and elastic net can all be implemented using the “glmnet” R package (Friedman, Hastie, and Tibshirani 2010) and the scikit-learn Python library. To learn more about the possibilities and limitations of the lasso, ridge, and elastic net algorithms, we recommend reading Zou and Hastie (2005), and for more information on these techniques in general, see Hastie, Friedman, and Tibshirani (2001).

10.5.3 Standardization for Lasso and Ridge

Since regularization in this context involves adding up the coefficients (squared for ridge and absolute value for lasso) and restricting the size of the coefficients based on this sum, if the original variables are on very different scales, the sum will be dominated by features with larger values. Thus, regardless of whether you are using ridge, lasso, or elastic net regularization, if your predictor variables are not already on the same scale, it is important to standardize them to a common scale before applying regularization (recall that this is not a requirement for the standard LS algorithm). Note that many built-in functions for implementing regularization tend to do this “under the hood” for you, but it is generally a good idea to pre-standardize your data yourself to make sure.

10.5.4 Cross-Validation for Choosing Regularization Hyperparameters

In Section 7.7.1 of Chapter 7, we introduced the CV technique for choosing the number of clusters. This same CV technique can be used to choose the value of the regularization hyperparameter, \(\lambda\) (the hyperparameter for the penalized version of the regularized LS algorithms). For a recap of the CV technique itself, refer back to Section 7.7.1, and recall that CV-based errors are helpful for comparing several versions of an algorithm for hyperparameter selection, but they do not give a realistic view of how the algorithm will perform on actual future or external data.

The procedure for using CV to choose a reasonable value of the regularization hyperparameter (for either lasso or ridge, using the penalty-term approach) is as follows:

1. Decide on a range of potential values for the penalty term, \(\lambda\). Note that many software implementations will do this for you.

2. Split the data into \(V\) (e.g., \(V = 10\)) nonoverlapping folds of approximately the same size.

3. Remove the first fold (this fold will play the role of the pseudo-validation set), and use the remaining \(V-1\) folds (which will play the role of the pseudo-training set) to train the regularized LS fit using each value of \(\lambda\).

4. Calculate the error (e.g., mean squared error (MSE)) for each of the regularized LS fits—one for each \(\lambda\)—using the first withheld CV-fold pseudo-validation set.

5. Replace the withheld first fold and now remove the second fold (the second fold will now play the role of the pseudo-validation set). Use the remaining \(V-1\) folds to train the algorithm for each value of \(\lambda\). Evaluate the fits using the withheld second fold (e.g., using MSE).

6. Repeat this process until all the \(V\) folds have been used as the withheld validation set, resulting in \(V\) measurements of the algorithm’s performance for each \(\lambda\).

7. For each value of \(\lambda\), calculate the average of the \(V\) errors. The average of the \(V\) errors is called the CV error.

8. Select the \(\lambda\) that had the lowest CV error, or that you judge to be the best (e.g., taking stability into consideration).

Figure 10.8 displays the average 10-fold CV MSE for a range of values of \(\lambda\) (the \(\lambda\) values—displayed on a log-scale—were chosen automatically by the cv.glmnet() function from the “glmnet” package in R) for ridge and lasso. The MSE for the ridge regularized fits start to increase around \(\log(\lambda) = 9\) (\(\lambda \approx 8,000\)), and the MSE for the lasso regularized fits start to increase as \(\log(\lambda)\) approaches \(7\) (\(\lambda \approx 1,000\)).

Figure 10.8: The CV MSE for a range of regularization hyperparameter choices for (a) ridge and (b) lasso. The hyperparameter value (\(x\)-axis) is presented on a log-scale, and the range of CV MSE values (minimum and maximum) for each lambda is shown using vertical lines.

The value that attains the lowest CV error is called \(\lambda_{min}\). However, rather than using the value that attains the smallest CV error, it is common to instead opt for a slightly larger value of \(\lambda\), just to enforce a little extra regularization (often this will help the model generalize better since its output will be slightly simpler). Thus, another common choice for \(\lambda\) is the largest value for which the MSE is within 1 standard error (SE) of the MSE for \(\lambda_{min}\) (the SE is defined as the SD scaled by the number of observations: \(SE = SD / \sqrt{n}\)). This value of \(\lambda\) is denoted by \(\lambda_{1SE}\). The log of the \(\lambda_{min}\) values for the ridge and lasso fits are 8.6 and 4.21, respectively. The log of the \(\lambda_{1SE}\) values for the ridge and lasso fits, however, are slightly larger, at 10.56 and 7.19, respectively. Note that since CV involves creating random folds, the values that you get each time you run this CV procedure will be slightly different.

An alternative stability-based technique for choosing the regularization hyperparameter, developed by Chinghway Lim and Bin Yu, is called Estimation Stability with Cross-Validation (ESCV) (Lim and Yu 2016).

The code for tuning and training the lasso and ridge predictive fits can be found in the 05_prediction_ls_adv.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the supplementary GitHub repository.

10.5.5 Lasso as a Feature Selection Technique

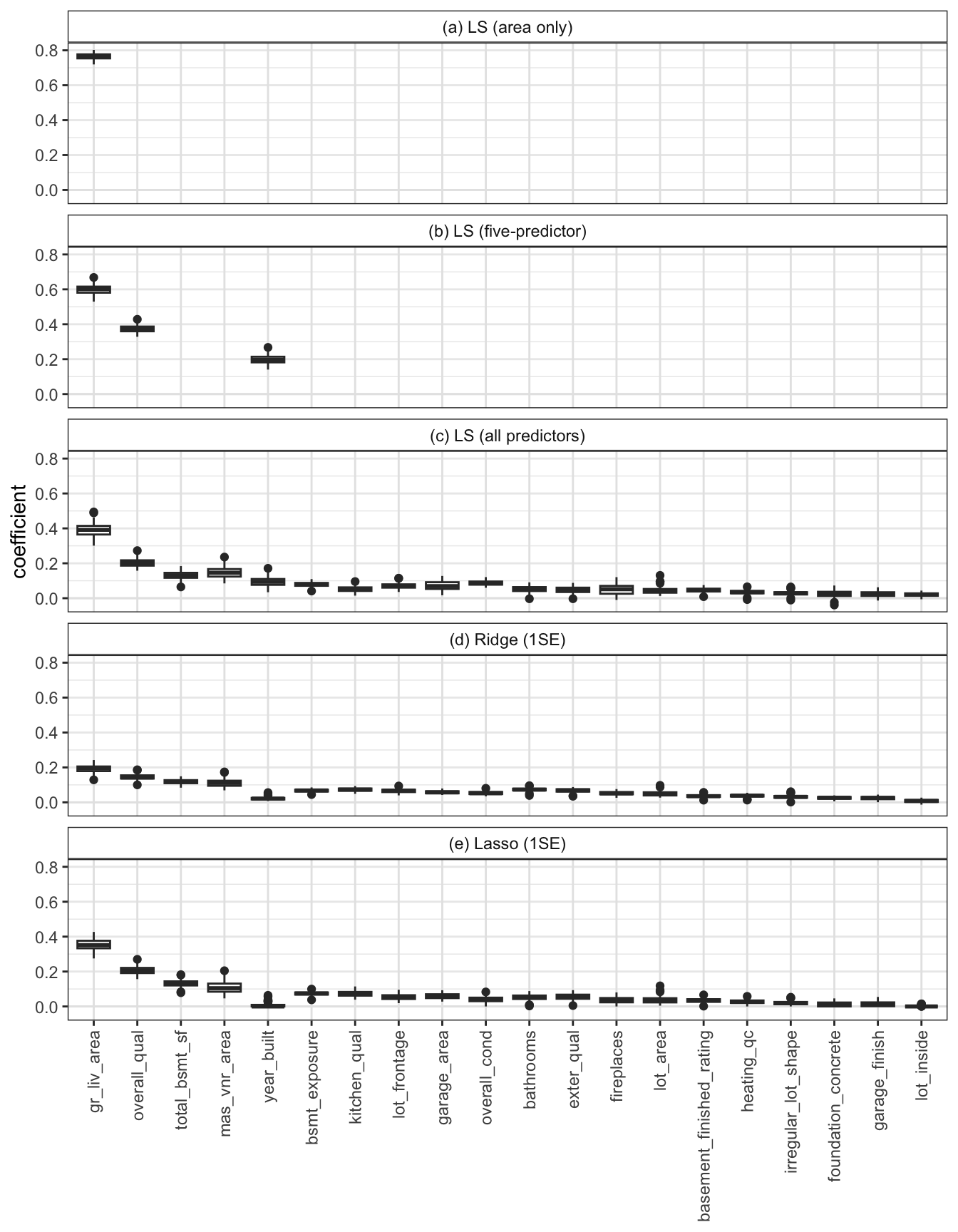
To get a sense of the amount of shrinkage that each regularized algorithm is applying to the coefficients, Figure 10.9 shows the value of the coefficients⁹ for the original LS (all feature) algorithm as light, transparent gray circles, and the corresponding regularized coefficients as black, opaque circles for the ridge fit with (a) \(\lambda_{min}\) and (b) \(\lambda_{1SE}\) and the lasso fit with (c) \(\lambda_{min}\) and (d) \(\lambda_{1SE}\). Each of these fits are based on the default cleaned/preprocessed version of the training data.

Figure 10.9: Line plots displaying the original and regularized coefficient values for each type of regularization: (a) ridge with the hyperparameter value that attains the smallest CV error; (b) ridge with the largest hyperparameter value that is within 1 SE of the smallest CV error; (c) lasso with the hyperparameter value that attains the smallest CV error; and (d) lasso with the largest hyperparameter value that is within 1 SE of the smallest CV error.

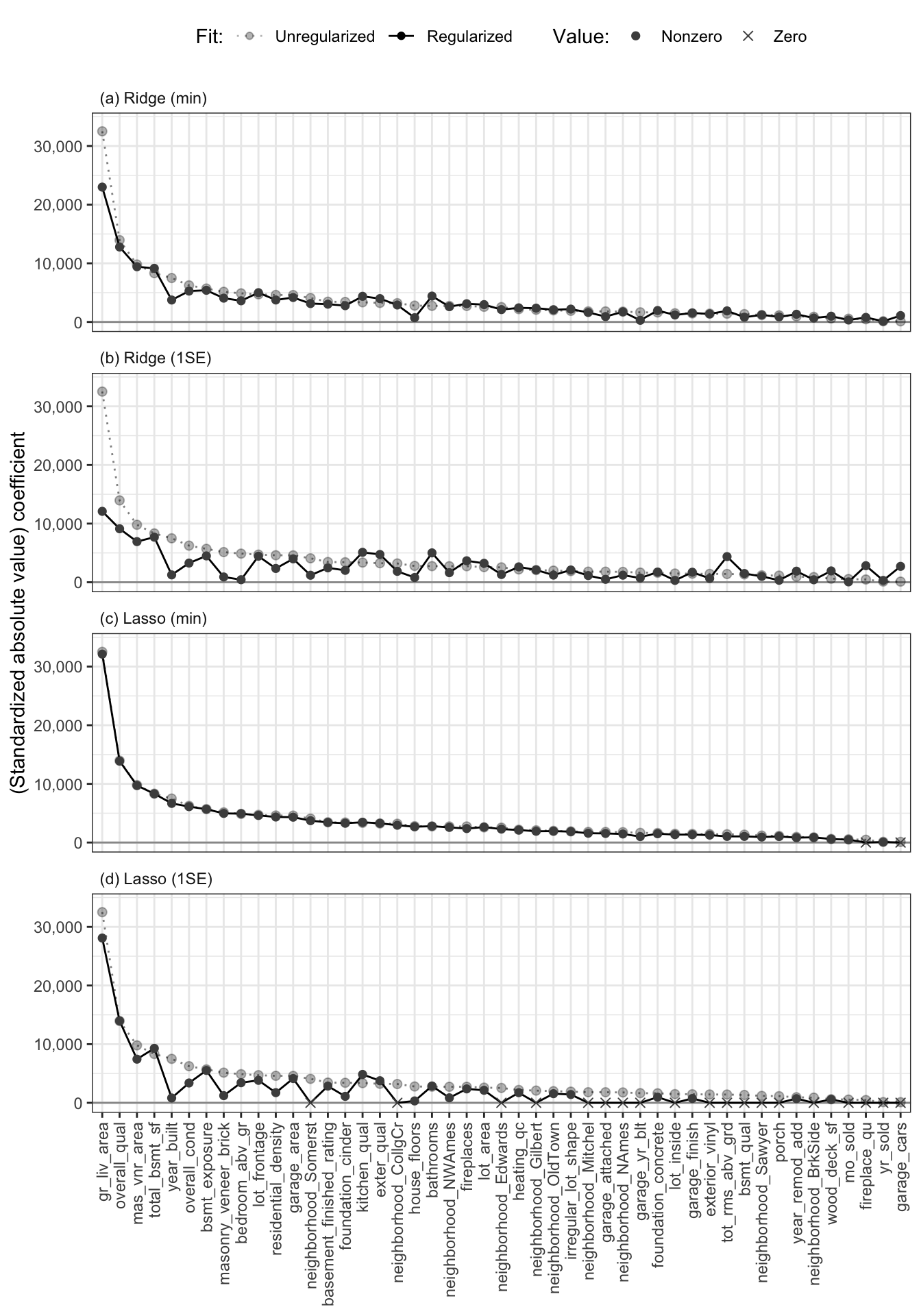
From Figure 10.9(c), it is clear that the lasso fit with \(\lambda_{min}\) implemented almost no shrinkage (implying that this regularization hyperparameter was not large enough to perform any meaningful regularization). The ridge fit with \(\lambda_{min}\) in Figure 10.9(a) involves slightly more regularization than the corresponding lasso fit with \(\lambda_{min}\), but most of the coefficients are still very similar to their unregularized counterparts.

On the other hand, Figure 10.9(d) shows that the lasso fit with \(\lambda_{1SE}\) shrank 19 of the 47 coefficients completely to zero (each coefficient that is exactly equal to zero is represented with an \(\times\) rather than a point). Note, however, that many of the coefficients of the ridge fit with \(\lambda_{1SE}\) in Figure 10.9(b) have been shrunk toward zero, but none of the ridge coefficients are exactly equal to zero.

Since the lasso algorithm will often shrink several coefficients all the way to zero, it can be used as a feature selection technique in which you remove all the features with lasso coefficients equal to zero and retrain a linear fit (e.g., using LS) with the remaining features (that had nonzero lasso coefficients).

10.6 PCS Evaluations

Now that we’ve introduced a range of extensions of the LS algorithm, let’s compare and evaluate them in terms of their validation set predictive performance (predictability) and their stability to data and cleaning/preprocessing judgment call perturbations.

The code for conducting and documenting these PCS analyses can be found in the 05_prediction_ls_adv.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the supplementary GitHub repository.

10.6.1 Predictability

The fits that we will evaluate in this section include the following:

• LS (area only): The original single-predictor living area fit from Chapter 9 (which we present here for comparison purposes)

• LS (five-predictors): The fit with five predictive features (living area, neighborhood, quality, year, bedrooms, and neighborhood) that was introduced at the beginning of this chapter

• LS (all predictors): The fit based on all the predictive features that are available in the data

• Ridge (1SE): The ridge (L2-regularized) fit with all the predictive features based on the \(\lambda_{1SE}\) hyperparameter

• Lasso (1SE): The lasso (L1-regularized) fit with all the predictive features based on the \(\lambda_{1SE}\) hyperparameter

Each of the fits in this predictability analysis section are trained using just one version of the cleaned and preprocessed training data and are evaluated on the equivalent cleaned and preprocessed validation dataset based on our default set of judgment calls. The default judgment calls that led to these particular cleaned/preprocessed versions of the training and validation data include implementing a missing value threshold of 0.5 and a maximum identical value threshold of 0.8; keeping the 10 largest neighborhoods and converting the rest to dummy variables; simplifying several variables; not performing any log transformations or correlation feature selection preprocessing steps; and converting several categorical variables directly to a numeric format (rather than creating dummy variables). See the code for our custom preProcessAmesData() function in the preProcessAmesData.R (or .py) file in the ames_houses/dslc_documentation/functions/ subfolder. This function is loaded into each of the analysis quarto/notebook files.

The validation set performance in terms of root-mean squared error (rMSE), mean absolute error (MAE), and the correlation between the observed and predicted response of these five linear fits are shown in Table 10.2.

Table 10.2: The rMSE, MAE, and correlation for the validation set predictions generated for the five linear predictive fits. Each fit is trained on one particular cleaned and preprocessed version of the Ames housing training data and is evaluated using the corresponding cleaned and preprocessed version of the validation data

Fit	rMSE	MAE	Correlation
LS (area only)	49,377	34,714	0.696
LS (five-predictor)	31,773	23,858	0.887
LS (all predictors)	23,267	17,332	0.942
Ridge (1SE)	23,607	16,901	0.94
Lasso (1SE)	23,219	16,725	0.941

Across each of these performance measures, it is first clear that increasing the number of predictive features included in the linear fit (the final three fits each involve all available predictive features) dramatically improves the predictive performance. When we use just the living area predictor variable to predict sale price (the first row of Table 10.2), the predicted and observed sale price responses have a validation set correlation of 0.696, whereas when we use five features (the second row of Table 10.2), this correlation jumps up to 0.887. Adding the remaining 40+ variables increases the correlation further to 0.942 (the third row of Table 10.2), which implies very good predictive performance. Regularization (in the form of ridge or lasso with \(\lambda_{1SE}\)) does not seem to meaningfully improve the validation set predictive performance compared with the original unregularized LS fit (all predictors).

10.6.2 Stability

Next, we will investigate the uncertainty associated with our predictions arising from the data collection procedure, as well as our own cleaning/preprocessing judgment calls, by examining the stability of the individual response predictions to relevant perturbations.

The code for conducting these stability analyses can be found in the 05_prediction_ls_adv.qmd (or .ipynb) file which can be found in the ames_houses/dslc_documentation/ subfolder of the supplementary GitHub repository. Note also that if you are a Python user, some of these stability simulations can be implemented using the “v-flow” library (Duncan et al. 2022).

10.6.2.1 Stability to Data Perturbations

First, we will investigate how stable our predictions are to data perturbations that are designed to reflect how our data may have been collected differently. Figure 10.10 displays prediction stability plots for each of the five fits. Each prediction stability plot shows the range of sale price predictions computed for 150 randomly selected validation set houses from each algorithm trained on 100 perturbed versions of the default cleaned/preprocessed training dataset.¹⁰

Figure 10.10: Prediction stability plots showing the range of predictions for 150 randomly selected validation set data points across the 100 perturbed LS fits with (a) one predictive feature (area); (b) five predictive features; (c) all available predictive features; (d) all predictive features and ridge regularization; and (e) all predictive features with lasso regularization.

The data perturbations that we used to produce these plots are the same as those we used in the previous chapter: a bootstrapped sample, as well as perturbations to the living area measurements in which random noise up to half an SD has been added to 30 percent of the living area measurements. To keep our stability analyses between each fit comparable, we did not add any additional perturbations to other predictor variables.

From Figure 10.10, it seems that although the predictions become more accurate as more predictor variables are added to the LS fit (see Section 10.6.1), the predictions also seem to become less stable (i.e., the line segments become wider). This observation can be quantified by observing that the average SD of the perturbed predictions for the single-predictor fit for the validation set houses, $2,168.77, is less than the average SD for the all-predictor fit, which is $5,827.40 (the average SD of the five-predictor fit predictions is in between, at $3,591.31). So while regularization did not appear to improve the predictive performance much, it did help slightly with stability: the average SD of the perturbed predictions for the ridge and lasso fits (with the \(\lambda_{1SE}\) hyperparameters) are $4,435.98 and $4,559.89, respectively, which are both less than for the unregularized all-predictor fit.

We will next investigate the stability of the coefficients. However, recall that to compare the coefficients to one another, we either need to standardize the coefficients (e.g., by dividing them by their bootstrapped SD) or we need to train our predictive algorithms using a version of the training data in which each variable has been pre-standardized (e.g., by subtracting the mean and dividing by the SD of each variable before computing the linear fit). For the following stability evaluation, we will take the latter approach (since it is computationally simpler).¹¹ Figure 10.11 shows the distribution of the 20 largest¹² coefficients across the 100 perturbed-training-data versions of each of the five fits. Fortunately, the coefficient values computed for each perturbed fit seem fairly stable (i.e., the boxplots are all fairly narrow).

Figure 10.11: Boxplots showing the distribution of the 20 largest (in absolute value) LS coefficients across the fits each trained on 100 perturbed versions of the training data. The variables were each standardized to a common scale before training the algorithms (so the coefficient values are comparable).

The code for conducting these data-perturbation stability analyses can be found in the 05_prediction_ls_adv.qmd (or .ipynb) file, which is in the ames_houses/dslc_documentation/ subfolder of the GitHub repository.

10.6.2.2 Stability to Data Cleaning and Pre-processing Judgment Call Perturbations

Next, recall that we made several preprocessing judgment calls when preparing the data for the LS algorithm. Examples of the judgment calls that we made include the number of neighborhoods to aggregate, converting ordered categorical levels to numeric values versus one-hot encoded binary variables (see Section 10.2), the missing value threshold for removing variables, whether to simplify several variables, whether to log-transform the response (see Section 10.3), and the correlation feature selection threshold (see Section 10.4).

In this section, we will investigate how much our predictions change when we make reasonable alternative choices for these judgment calls. A detailed exploration of the judgment calls that we made can be found in the 01_cleaning.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the supplementary GitHub repository. The code for the stability analysis that we will conduct in this section can be found in the 05_prediction_ls_adv.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder.

Since most of the judgment calls are only relevant to fits that involve all the predictive features, we will focus our stability analysis in this section on this all-feature LS fit and the ridge and lasso fits (with \(\lambda_{1SE}\)). Therefore, in total, we consider 336 cleaning/preprocessing judgment call combinations (based on six judgment calls, each with two or three alternative options and ignoring cleaned/preprocessed data duplicates that are generated by multiple judgment call combinations) in this stability analysis. Before we begin, we will first conduct predictability screening to identify any judgment calls that lead to particularly poor validation set predictive performance (since including these poorly performing fits in our stability analysis may give us an unreasonably unfavorable view of the stability of our predictions). Figure 10.12 shows the range of validation set correlation values for the LS (all predictor), ridge, and lasso fits for each judgment call option.

Figure 10.12: Boxplots demonstrating the distributions of the LS, lasso, and ridge validation set correlation performance, where each algorithm is trained using various combinations of the following six preprocessing judgment calls: (a) converting ordered categorical variables to dummy variables, numeric variables, or a simplified version of the dummy variables; (b) the choice of missing value threshold above which to remove features; (c) the choice of how many neighborhoods to aggregate; (d) whether to simplify several variables; (e) whether to apply a log or square-root transformation to the response; and (f) whether to apply a correlation-based feature selection (a threshold of 0 corresponds to no feature selection).

While all the fits yield an observed-predicted response correlation of above 0.91 for the validations set houses (which is quite good correlation performance), there are clearly some judgment calls that led to decreased/increased predictive performance. For instance, it is clear from Figure 10.12(e) that applying a log transformation to the response variable substantially improves the predictive performance (relative to not transforming the response), and Figure 10.12(f) indicates that implementing a correlation feature selection procedure (with a threshold of 0.5) substantially decreases the prediction performance. The other judgment calls don’t seem to have much of an impact on the predictive performance.

Our predictability screening will therefore remove all fits that have an observed-predicted response correlation of less than 0.93 on the validation set (note that this threshold choice is itself a judgment call). Out of a total of 336 cleaning/preprocessing judgment call–perturbed fits for each algorithm, 304 of the LS fits, 304 of the ridge fits, and 296 of the lasso fits pass this predictability screening. Note that the more restrictive our predictability screening, the narrower our prediction ranges will be. Thus, to compare the stability of various algorithmic fits, they need to each be subject to the same predictability screening process.

Figure 10.13 presents a prediction stability plot for each of the three fits (LS, ridge, and lasso, each using all available predictive features) conveying the range of the predictions across the preprocessing judgment call–perturbed training set fits that passed our predictability screening. Interestingly, even after filtering just to the fits that pass the predictability screening, there appears to be more instability arising from these preprocessing judgment call perturbations than there was from the data (sampling and noise-based) perturbations that we examined in Section 10.6.2.1. Again, regularization seems to improve the stability of the predictions: the average SD of the perturbed response predictions for the LS, ridge, and lasso fits are $8,831, $7,787, and $7,258, respectively.

Figure 10.13: Prediction stability plots showing the range of the predictions generated for 150 randomly selected validation set data points for (a) the LS fits (with all predictors); (b) the ridge fits; and (c) the lasso fits, each trained using versions of the training set that are cleaned and preprocessed using different combinations of the cleaning/preprocessing judgment calls. This stability analysis only includes fits that pass predictability screening corresponding to a validation set correlation of at least 0.93.

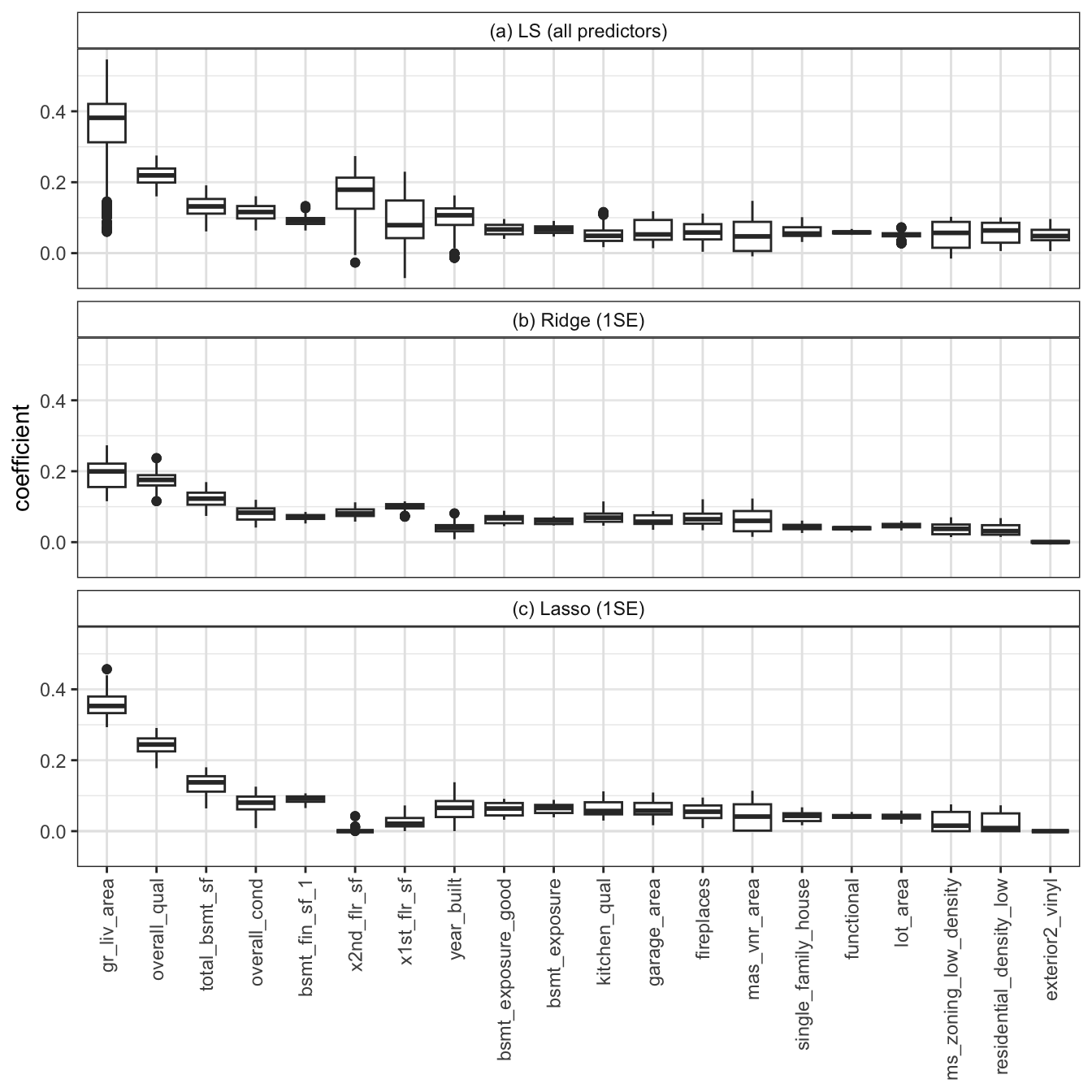
Figure 10.14 shows the distribution of the data cleaning/preprocessing judgment call-perturbed coefficients for the 20 features with the largest (absolute value) magnitude. Since the boxplots for the unregularized LS fit in panel (a) are generally wider than their regularized counterparts in panels (b) and (c), this figure reinforces the notion that regularization improves the stability of the LS fits.

Figure 10.14: Boxplots showing the distribution of the 20 largest (in absolute value) LS coefficients across the fits trained on the cleaning/preprocessing judgment call–perturbed versions of the training data that pass predictability screening. The variables were each standardized to a common scale before training the algorithms (so that the coefficient values are comparable).

For the code for these stability analyses (and some additional stability analyses), see the 05_prediction_ls_adv.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the supplementary GitHub repository.

10.7 Appendix: Matrix Formulation of a Linear Fit

The following is one way to represent a linear fit with \(p\) predictors:

\[y_i = b_0 + b_1x_{i1} + b_2x_{i2} + ... + b_{p} x_{ip},\]

where \(i = 1, ..., n\). However, this same fit can be written in a matrix format as follows:

\[ Y = X\beta, \tag{10.9}\]

where

\[ Y = \left[\begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n \end{array}\right] \tag{10.10}\]

is the \(n \times 1\) column vector of responses for the \(n\) data points,

\[ \beta = \left[\begin{array}{c} b_0\\ b_1\\ b_2\\ \vdots\\ b_{p} \end{array}\right] \tag{10.11}\]

is the \((p + 1) \times 1\) column vector of coefficient values for the \(p\) predictive features and an intercept term, and

\[ X = \left[\begin{array}{ccccc} 1 & x_{11} & x_{12} & \dots & x_{1p}\\ 1 & x_{21} & x_{22} & \dots & x_{2p}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & x_{n1} & x_{n2} & \dots & x_{np}\\ \end{array}\right] \tag{10.12}\]

is the \(n \times (p + 1)\) predictive feature matrix for the \(n\) data points and \(p\) predictive features (plus an intercept term, corresponding to the first column).

The matrix formulation of the LS squared loss is given by

\[ (Y - X\beta)^T(Y - X \beta), \tag{10.13}\]

and the formula for the coefficient vector that minimizes the LS squared loss is given by

\[ \beta = (X^TX)^{-1}X^TY. \tag{10.14}\]

If you’re handy with matrices and calculus, you should try and prove this result yourself, as well as show that these matrix computations yield the formulas that we introduced in the previous chapter (Equation 9.9 and Equation 9.10) when \(p = 1\) (i.e., there is one predictive feature and an intercept term). If you’re not, don’t worry because the lm() function in R and the linear_model.LinearRegression() class from the scikit-learn Python library will implement these formulas for you!

Note that the ridge-regularized LS loss function can be written as

\[ (Y - X\beta)^T(Y - X\beta) + \lambda \beta^T \beta, \tag{10.15}\]

and an exact solution for minimizing the ridge-regularized LS loss function can be computed using the matrix formulation

\[ \beta = (X^TX + \lambda I)^{-1}X^TY. \tag{10.16}\]

Unfortunately, there is no exact solution for the lasso.

Exercises

True or False Exercises

For each question, specify whether the answer is true or false (briefly justify your answers).

1. The magnitude of the LS coefficient of a predictive feature corresponds to how important the feature is for generating the prediction.

2. The LS algorithm cannot be applied directly to data with categorical predictor variables without modifying the data.

3. Correlation feature selection can be used for data that has binary predictor variables.

4. Increasing the number of predictive features in a predictive fit will always improve the predictive performance.

5. The LS algorithm can only be used to train linear relationships between a response and predictor variable.

6. The preprocessing judgment calls that you make can affect your predictive performance.

7. Overfitting to the training data happens when your predictive fit captures very specific patterns that exist only in the training data and do not generalize to other similar data.

8. The best ridge and lasso regularization hyperparameter is the value that yields the smallest CV error.

9. More regularization means that regularized coefficients will be closer to the original un-regularized LS coefficients.

10. It makes more sense to use L2 (ridge) regularization than L1 (lasso) regularization for the LS algorithm because the LS algorithm involves minimizing an L2 (squared) loss function.

Conceptual Exercises

11. Explain why it is common to remove one level of a categorical variable to act as a reference level when creating one-hot encoded (dummy) binary variables.

12. Define collinearity in the context of prediction problems and discuss why it is an issue.

13. Describe one cause of overfitting and describe an analysis that you could conduct to identify whether your predictive fit is overfitting to the training data.

14. Explain how you could use the lasso algorithm as a feature selection technique.

15. Describe (in lay terms) how ridge regularization simplifies and stabilizes the LS solution.

Mathematical Exercises

16. Suppose that you have reason to believe that your response variable, \(y\), has an exponential relationship with a predictor variable, \(x\) (i.e., \(e^{x}\) is a good predictor of \(y\)).

    1. Write the format of a reasonable predictive fit (for predicting \(y\) based on \(x\)) that captures this exponential relationship that could be computed by the LS algorithm.

    2. Write the corresponding LS loss function.

17. Suppose that you have produced a linear fit of the form \[\textrm{predicted price} = b_0 + b_1\textrm{area} + b_2\textrm{quality} + b_3 \textrm{year} + b_4 \textrm{bedrooms}\]

    1. Show that the predicted price of a house that has an area of \(0\) square feet, a quality score of \(0\), was built in the year \(0\), and has \(0\) bedrooms is equal to \(b_0\).

    2. Show that the predicted price of a house will increase by \(b_1\) if we increase the living area of the house by a value of 1, without changing the value of the other predictive features.

Coding Exercises

18. In this chapter, we have focused solely on the LS algorithm, but many of the topics introduced in this chapter apply equally well to the LAD algorithm.

    1. Use the LAD algorithm (e.g., using the lad() function from the “L1pack’’ R package, setting method = "EM", or the Python linear_model.LADRegression() class from the sklego library) to generate a predictive fit for house price based on all the available predictive features. You may use the default cleaned/preprocessed version of the data that we used throughout this chapter, or you may use your own. You may want to write your code in a new section at the end of the 05_prediction_ls_adv.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the supplementary GitHub repository.

    2. Compare the validation set predictive performance of your LAD fit with the corresponding LS (all predictors) fit (e.g., using rMSE, MAE, and correlation).

    3. Compare the coefficients of your LAD fit with the coefficients of the LS fit.

    4. Create standardized versions of the LAD and LS coefficients using the bootstrap technique introduced in Section 10.1.2 (i.e., by estimating the SD of the coefficients by retraining the algorithms on bootstrapped training datasets sampled with replacement). Compare the standardized LS and LAD coefficients. Do your conclusions change?

    5. Assess the stability of your LAD fit (relative to the LS fit) by visualizing the range of predictions generated across (i) data- and (ii) judgment call-perturbations using prediction stability plots. You may want to edit a copy of the relevant code in the 05_prediction_ls_adv.qmd (or .ipynb) file in the ames_houses/dslc_documentation/ subfolder of the supplementary GitHub repository.

Project Exercises

19. Predicting happiness (continued) This project extends the happiness prediction project from the previous chapter. The goal will be to create a more sophisticated LS fit than the previous single-predictor fit. The files for this project can be found in the exercises/happiness/ folder on the supplementary GitHub repository.

    1. In the dslc_documentation/01_cleaning.qmd (or .ipynb) file, conduct a data cleaning and preprocessing examination using all variables in the data. Modify the data cleaning function (in the cleanHappiness.R (or .py) file in the dslc_documentation/functions/ subfolder) and/or write a preprocessing function to preprocess the data (you may want to just have one function that both cleans and preprocesses the data, or separate cleaning and preprocessing functions), and save your functions in relevant .R (or .py) files in the dslc_documentation/functions folder. If you created it in the previous chapter’s exercise, be sure to update the prepareHappiness.R (or .py) file in the dslc_documentation/functions/ subfolder that implements your cleaning/preprocessing procedure. Document any judgment calls that you make (and possible alternatives) in the relevant DSLC documentation files.

    2. Based on the splitting strategy you used for this project last chapter, split the data into training, validation, and test sets, and create cleaned/preprocessed versions of each dataset (we suggest writing this code in the prepareHappiness.R (or .py) file in the dslc_documentation/functions/ subfolder).

    3. In the dslc_documentation/02_eda.qmd (or .ipynb) file, conduct an exploratory data analysis (EDA) on the training set, particularly to investigate how a range of different features are related to the happiness score (you can skip this if your EDA from the previous chapter involved all the predictors).

    4. In the dslc_documentation/03_prediction.qmd (or .ipynb) file, use the LS, ridge, and lasso algorithms to compute a linear predictive fit with multiple features for the happiness score using your pre-processed training data. Be sure to keep a record of all predictive fits that you try (you will be able to filter out poorly performing fits later).

    5. In the dslc_documentation/03_prediction.qmd (or .ipynb) file, conduct a PCS analysis of your fits, and compare your multipredictor fits’ performance to the single-predictor fit from the previous chapter.

    6. In the dslc_documentation/03_prediction.qmd (or .ipynb) file, compute standardized versions (using the bootstrap) of the coefficients for your LS fits to identify which variables are most important for predicting happiness.

References

Duncan, James, Rush Kapoor, Abhineet Agarwal, Chandan Singh, and Bin Yu. 2022. “VeridicalFlow: A Python Package for Building Trustworthy Data Science Pipelines with PCS.” Journal of Open Source Software 7 (69): 3895.

Freedman, David A. 2009. Statistical Models: Theory and Practice. Cambridge University Press.

Friedman, Jerome, Trevor Hastie, and Rob Tibshirani. 2010. “Regularization Paths for Generalized Linear Models via Coordinate Descent.” Journal of Statistical Software 33 (1): 1–22.

Hastie, Trevor, Jerome Friedman, and Robert Tibshirani. 2001. The Elements of Statistical Learning. Springer. Springer.

Lim, Chinghway, and Bin Yu. 2016. “Estimation Stability with Cross-Validation (ESCV).” Journal of Computational and Graphical Statistics 25 (2): 464–92.

Stoica, P., and Y. Selen. 2004. “Model-Order Selection: A Review of Information Criterion Rules.” IEEE Signal Processing Magazine 21 (4): 36–47.

Zou, Hui, and Trevor Hastie. 2005. “Regularization and Variable Selection via the Elastic Net.” Journal of the Royal Statistical Society. Series B (Statistical Methodology) 67 (2): 301–20.

---

1. Recall that we split the Ames housing data into three parts: the training data for computing the coefficient values, the validation data for evaluating and comparing the predictive fits we produce, and the test data, which we will use in Chapter 13 to evaluate the final predictions.

2. This is the only part of our predictability, computability, and stability (PCS) stability assessments that is considered in traditional statistical inference. See Freedman (2009) for an introduction to this topic.

3. We have filtered the training data just to these five neighborhoods for this example.

4. The Gaussian distribution is symmetric, but a symmetric distribution does not necessarily imply Gaussianity.

5. You might be worried that the curve in this graph doesn’t look quite like a standard quadratic curve, but it is just that the base of the quadratic curve is to the left of the data, so the left arm is cut off in the plot.

6. You may still be able to find an approximate solution using an optimization technique, such as gradient descent.

7. “Parameters” are explicitly used when computing the final predictions (e.g., the \(b\) parameters in \(\textrm{prediction} = b_0 + b_1 \textrm{area}\)), whereas “hyperparameters” are only used during training.

8. The L0-norm of a vector corresponds to the number of nonzero entries it contains.

9. Each feature has been pre-standardized so that the coefficients are comparable.

10. Note that the \(\lambda\) hyperparameter must be chosen using CV for each perturbed fit.

11. To standardize the validation data, we will use the mean and SDs computed from the training data.

12. In terms of the absolute value of the LS (all predictors) fit coefficients.