11 Binary Responses and Logistic Regression
This is the Open Access web version of Veridical Data Science. A print version of this book is published by MIT Press. This work and associated materials are subject to a Creative Commons CC-BY-NC-ND license.
In our prediction problems so far, we have only considered problems that involve predicting a continuous response (house price is a continuous variable that can take a range of numeric values). However, many prediction problems in data science involve instead predicting a binary response, where each observation’s response falls into one of two categories, such as “yes” or “no.” A binary response is often referred to as the class label of the observation. Prediction problems with binary responses are often called classification problems because they involve classifying each observation as belonging to one of the two classes.
To introduce binary prediction problems, we will switch to a new project: the online shopping purchase prediction project.
11.1 The Online Shopping Purchase Prediction Project
One of the biggest employers of data scientists are e-commerce retailers that sell products online (i.e., online stores). In this chapter, we will place ourselves in the role of a data scientist trying to develop an algorithm that can predict which user sessions on a particular e-commerce website will end in a purchase. Our goal is to use this algorithm to predict the purchase intent of future user sessions on the site. If you can predict whether a new visitor is likely to make a purchase, then you can use this information to, say, make more generous offers to users whom you predict are less likely to make a purchase (hopefully thus increasing the chance that they will make a purchase).
11.1.1 Data Source
The data that we will use—the Online Shoppers Purchasing Intention Dataset—has been made publicly available by Sakar et al. (2019) and can be downloaded from the UCI Machine Learning repository. The data is based on 12,330 visitor sessions for an e-commerce store’s website across a 1-year period. As is often the case with public data, the documentation provided with it is somewhat ambiguous. In this case, we are not even told which website the data came from or what is being sold. (This means that we would never use this dataset to make any actual real-world decisions, but it serves us well for demonstration purposes in this book!)
The dataset contains 17 predictive features and a response variable. The predictive features for each user session include a set of variables describing the number of pages of each type (“administrative,” “informational,” and “product-related”) visited by the user during the session, and the amount of time they spent on each type of page (“administrative duration,” “informational duration,” and “product-related duration”).
Next, there is a set of features collected for each session from Google Analytics, including the average “bounce rate” of each page visited (the percentage of users who enter the site on the page and then immediately leave the site), the average “exit rate” of each page visited (the proportion of views of the page that corresponded to the final page in the user session), and the average “page value” of each page visited (a measure of how much a page contributes to the site’s revenue) during the user’s session. For more information about data from Google Analytics, see Clifton (2012).
The data also includes information about the “operating system” involved in the session, the web “browser” used, the “region” that the user is in, the “traffic type” (how the user arrived at the site, such as an advertisement, a direct URL, etc.), and the “visitor type” (whether the user is a new or returning visitor). Unfortunately, many of these variables are numerically coded, and there is no information on what each numeric entry corresponds to (e.g., we do not know which operating system is represented by “1,” which one is represented by “2,” etc.).
Then there are also several data-related features, including “month” (the month in which the session occurs), “weekend” (whether the session takes place on a weekend), and “special day” (an indicator of how close the date of the session is to a special day, such as Mother’s Day, Valentine’s Day, etc.).
Finally, the binary response variable, “purchase”,1 corresponds to whether a purchase was made during the session (i.e., whether the session led to any revenue for the site).
Unfortunately, the background information that was provided along with this dataset is very limited (we did try to email the authors for more information, but we did not receive a response). Since we don’t know whether the data has been pre-cleaned or how the data was collected, we are going to have to make a lot of assumptions.
11.1.2 A Predictability Evaluation Plan
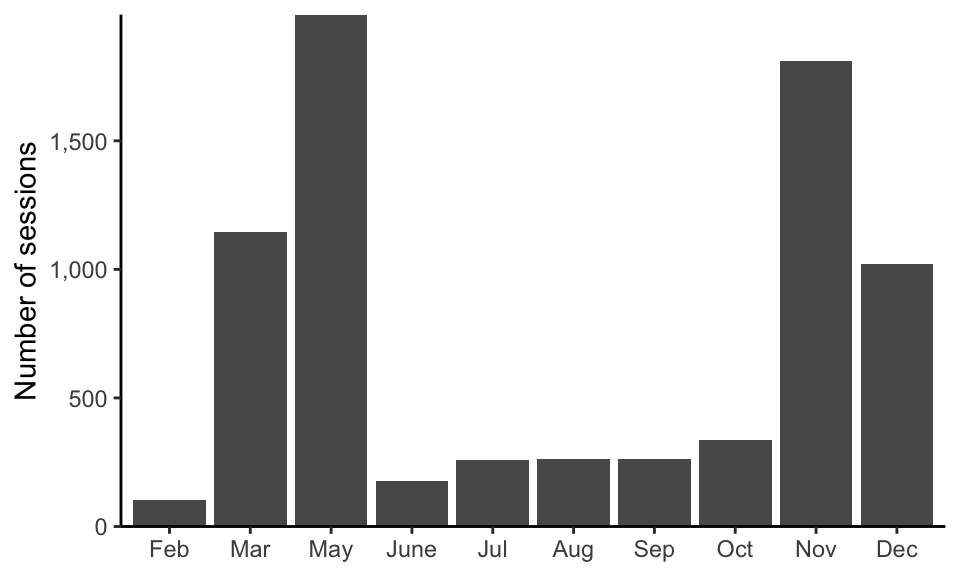
Before we dive into developing predictive fits, we need to first make a plan for evaluating the predictability of our fits. Recall that the ideal predictability assessment involves evaluating our fits using future/external data. However, since we don’t have access to any future/external data from additional user sessions from the online store, we will need to split the shopping data into training (60 percent), validation (20 percent), and test sets (20 percent). However, as is often the case, the decision on how to split our data into training, validation, and test sets is not immediately obvious. Since the data is collected over time and our goal is to make purchase intent predictions during the following year, it might seem as though it would make sense to conduct a time-based split, where the first 60 percent of sessions form the training data and the final 40 percent of sessions form the validation and test set data. However, for this particular example, the data spans only one year, and online shopping patterns are annually cyclical (e.g., many stores will see a surge of customers during sales or holiday periods that occur at the same time each year; see Figure 11.1). Since our goal is to predict the purchase intent of sessions that take place during all the months of the following year, the idea of using just the last few months of the current year to form the validation and test sets doesn’t feel representative of this future scenario in which we plan to hypothetically apply our algorithm.2
If a time-based split doesn’t quite make sense, what about using a random split to form the training, validation, and test sets? If we can assume that each session is independent (i.e., that one session’s purchase response doesn’t depend on any other session’s response), then a random split would indeed be reasonable. However, this assumption ignores the fact that many of the sessions involve return visitors (so there may be multiple sessions that involve the same visitor, which introduces a dependence). However, since many of the following year’s sessions may also involve returning visitors, we nonetheless feel that a randomly chosen validation and test set would be reasonably representative of the hypothetical following year’s sessions (assuming that the purchase trends remain fairly stable from one year to the next). For now, we will simply make this assumption, but in practice, we recommend checking that this stability assumption is true (e.g., using domain knowledge of customer behaviors and economic conditions).
11.1.3 Cleaning and Preprocessing the Online Shopping Dataset
Not only do we not know much about how the data was collected, but we also have no idea whether this data has already been cleaned/preprocessed in any way. Regardless, an initial data cleaning examination revealed several ambiguities and inconsistencies that prompted us to create several action items. Before reading how we cleaned and explored the data, we suggest that you spend some time exploring and cleaning this online shopping dataset yourself. The data and our code for cleaning and preprocessing this data can be found in the online_shopping/ folder of the supplementary GitHub repository.
An example of an ambiguity that we identified concerns the “month” variable. Figure 11.1 shows the number of sessions reported in the data each month. Do you notice anything odd about this bar plot? For instance, where are January and April? Did everyone collectively decide to boycott the website during those months? Was the website down? Or were these months simply excluded (or accidentally deleted) from the data? Since we are not in touch with the people who collected the data, there is unfortunately no way to know the answers to these questions. This dataset is yet another excellent example of the unresolvable ambiguities that tend to arise when you work with publicly available datasets where it is not possible to get in touch with the people who originally collected the data.

Fortunately, however, there were several other ambiguities that we were able to resolve (by making judgment calls about the most reasonable ways to handle them) during data cleaning and preprocessing. For example, we replaced negative duration values with either missing values or 0s, and we converted categorical variables that were originally represented numerically (such as the “browser,” “region,” and “traffic type” variables) to more appropriately formatted categorical variables (which were then converted to one-hot encoded, binary dummy variables during preprocessing since the binary prediction algorithms that we will introduce in this chapter do not accept categorical features).
During our explorations, we also noticed that most of the numeric variables have very skewed (asymmetrical) distributions. Figure 11.2 shows the skewed distributions of the “administrative duration,” “informational duration,” and “product-related duration” variables (the \(x\)-axis in each plot extends far beyond the visible bars, indicating the presence of a small number of very large values). We thus added a preprocessing option to apply a logarithmic transformation to each relevant feature to make their distributions more symmetric, which can sometimes improve the predictive power of the features (see Section 10.3 in Chapter 10).
A complete summary of the cleaning and preprocessing explorations and action items (and the corresponding judgment calls that we made) can be found in the 01_cleaning.qmd (or .ipynb) file in the online_shopping/dslc_documentation/ subfolder of the supplementary GitHub repository.

Table 11.1 shows a subset of the variables from our default version of the cleaned/preprocessed dataset for a random sample of 20 sessions (where, due to space constraints, we are showing only 13 of the 19 variables, and we have not converted the categorical variables to one-hot encoded binary variables).
| Purchase | Administrative | Administrative duration | Product related | Product related duration | Bounce rates | Exit rates | Page values | Special day | Month | Weekend | Return visitor | Browser |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.0 | 8 | 8.3 | 0.017 | 0.03 | 0.0 | 0 | Dec | 1 | 1 | 8 |
| 0 | 1 | 0.2 | 34 | 15.7 | 0.000 | 0.01 | 0.0 | 0 | May | 0 | 1 | 2 |
| 0 | 0 | 0.0 | 28 | 8.9 | 0.000 | 0.02 | 0.0 | 1 | May | 1 | 1 | 4 |
| 1 | 1 | 0.5 | 20 | 15.4 | 0.000 | 0.01 | 103.1 | 0 | Dec | 0 | 0 | 2 |
| 1 | 6 | 0.8 | 14 | 14.3 | 0.000 | 0.01 | 0.0 | 0 | Oct | 0 | 0 | 1 |
| 0 | 2 | 1.3 | 12 | 4.4 | 0.029 | 0.03 | 0.0 | 0 | Mar | 0 | 1 | 1 |
| 0 | 0 | 0.0 | 6 | 2.2 | 0.067 | 0.09 | 0.0 | 0 | May | 0 | 1 | 1 |
| 0 | 1 | 0.9 | 17 | 13.9 | 0.033 | 0.06 | 0.0 | 0 | May | 0 | 1 | 2 |
| 0 | 0 | 0.0 | 7 | 0.9 | 0.000 | 0.04 | 0.0 | 1 | May | 1 | 1 | 2 |
| 0 | 12 | 3.9 | 22 | 8.4 | 0.000 | 0.00 | 0.0 | 0 | Sep | 0 | 0 | 1 |
| 0 | 0 | 0.0 | 7 | 1.0 | 0.000 | 0.06 | 0.0 | 0 | Nov | 0 | 1 | 6 |
| 0 | 2 | 1.4 | 21 | 11.8 | 0.012 | 0.03 | 0.0 | 0 | Nov | 0 | 1 | 4 |
| 0 | 3 | 1.2 | 24 | 6.1 | 0.000 | 0.01 | 0.0 | 0 | Sep | 0 | 0 | 2 |
| 0 | 2 | 5.1 | 13 | 3.0 | 0.000 | 0.02 | 0.0 | 0 | Oct | 1 | 1 | 1 |
| 0 | 0 | 0.0 | 2 | 0.9 | 0.000 | 0.10 | 0.0 | 0 | Feb | 0 | 1 | 1 |
| 0 | 5 | 4.3 | 4 | 7.0 | 0.000 | 0.01 | 0.0 | 0 | Sep | 0 | 0 | 1 |
| 1 | 0 | 0.0 | 19 | 18.7 | 0.021 | 0.05 | 11.4 | 0 | May | 1 | 1 | 1 |
| 1 | 2 | 0.3 | 15 | 12.6 | 0.013 | 0.06 | 29.2 | 0 | Mar | 0 | 1 | 10 |
| 0 | 0 | 0.0 | 9 | 3.4 | 0.000 | 0.00 | 0.0 | 0 | Nov | 0 | 1 | 1 |
| 0 | 0 | 0.0 | 19 | 8.6 | 0.011 | 0.03 | 0.0 | 0 | Dec | 1 | 1 | 1 |
11.1.4 Exploring the Online Shopping Data
Next, we conducted an exploratory data analysis (EDA) of our cleaned/preprocessed online shopping data. Some exploratory questions that we asked of the data included “Which months have the highest purchase rate?” “In what months do the `special days’ occur?” “Do the number of purchases across sessions increase during months with ‘special days’?” “Do the proportion of sessions with purchases differ by browser, operating system, region, or type of traffic?” We recommend that you conduct some of your own explorations of the training data to try and answer some of these questions, and to ask some of your own too.
Through our explorations, we also discovered that:
16 percent of sessions resulted in a purchase (84 percent did not).
The “special days” occur in May (perhaps for Mother’s Day?) and February (perhaps for Valentine’s Day?), but surprisingly, it seems as though fewer purchases are made around these days.
November has the highest proportion of sessions resulting in a purchase.
Sessions that spent more time on product-related pages were more likely to make a purchase.
We also created an explanatory plot, shown in Figure 11.3, designed to show (e.g., to company executives) that sessions that spend more than 1 hour on product-related pages are twice as likely to result in a purchase than sessions that spend less than 1 hour on product-related pages. To keep the message of the plot as simple as possible, rather than presenting the entire distribution of the product-related page session durations, we simplified this information by instead using a binary thresholded version of the product-related duration variable to compare the purchase rates of pages that spent more than 1 hour on product-related pages with the purchase rate for pages that spent less than 1 hour on product-related pages.
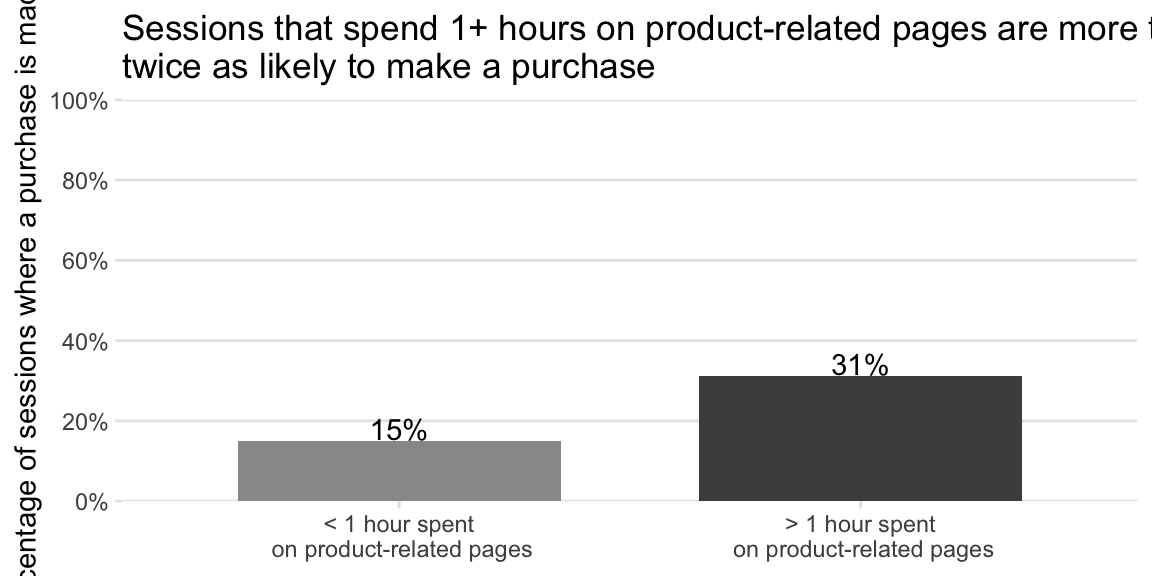
One way to test the stability of this result is to change the binary threshold of 1 hour and demonstrate that the overall finding (that sessions that spent more time on product-related pages tended to be more likely to result in a purchase) doesn’t change dramatically. When we changed the threshold to 1.5 hours, we obtained very similar results. The code that underlies our exploratory findings can be found in the 02_eda.qmd (or .ipynb) file in the online_shopping/dslc_documentation/ subfolder of the supplementary GitHub repository.
11.2 Least Squares for Binary Prediction
In Chapter 9, we introduced the Least Squares (LS) algorithm for predicting continuous response variables that involve a range of numeric values. Our goal now, however, is to generate predictions of binary response variables that can take only two possible values (e.g., purchase/no purchase). Rather than reinventing the wheel, let’s first try to apply the LS algorithm directly to our binary response prediction problem. This involves encoding our binary response variable numerically (e.g., by setting the response to \(1\) if the user makes a purchase and to \(0\) if the user does not make a purchase).3
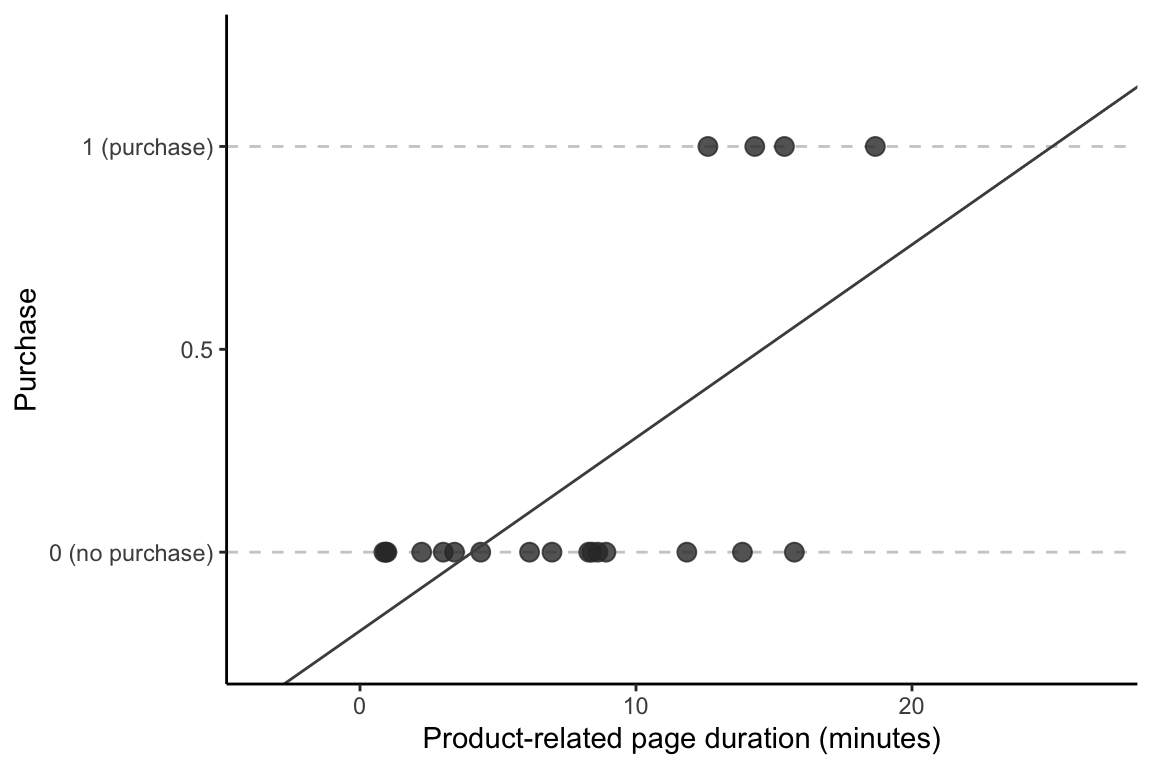
Let’s demonstrate using the 20 sessions in Table 11.1. If we train the LS algorithm to predict the binary numeric “purchase” response variable using the “product-related page duration” variable as the sole predictor, we get the fitted line in Figure 11.4. Note that for each point (session), the observed response (\(y\)-coordinate of the point) is either 0 or 1, but the LS-based predicted response (the \(y\)-coordinates of the fitted line) has no such constraints. Instead, the predictions based on the LS fitted line (i.e., the \(y\)-coordinates of the line) are arbitrary numeric values such as 0.235, or 1.155. The LS fitted line in Figure 11.4 is given by
\[\begin{align*} \textrm{predicted purchase} = -0.194 + 0.048\times \textrm{product-related duration}, \end{align*}\]
where “product-related duration” is the number of minutes spent on product-related pages during the session. Based on this linear fit, the predicted purchase response of a session that spent \(20\) minutes on product-related pages is \(0.76\). Since we have not changed the LS algorithm in any way to indicate that the response should be equal to only 0 or 1, the LS algorithm is returning unconstrained continuous numeric response predictions. How should we interpret this purchase response prediction since it is not equal to either of the allowable observed response values of 0 (no purchase) or 1 (purchase)?
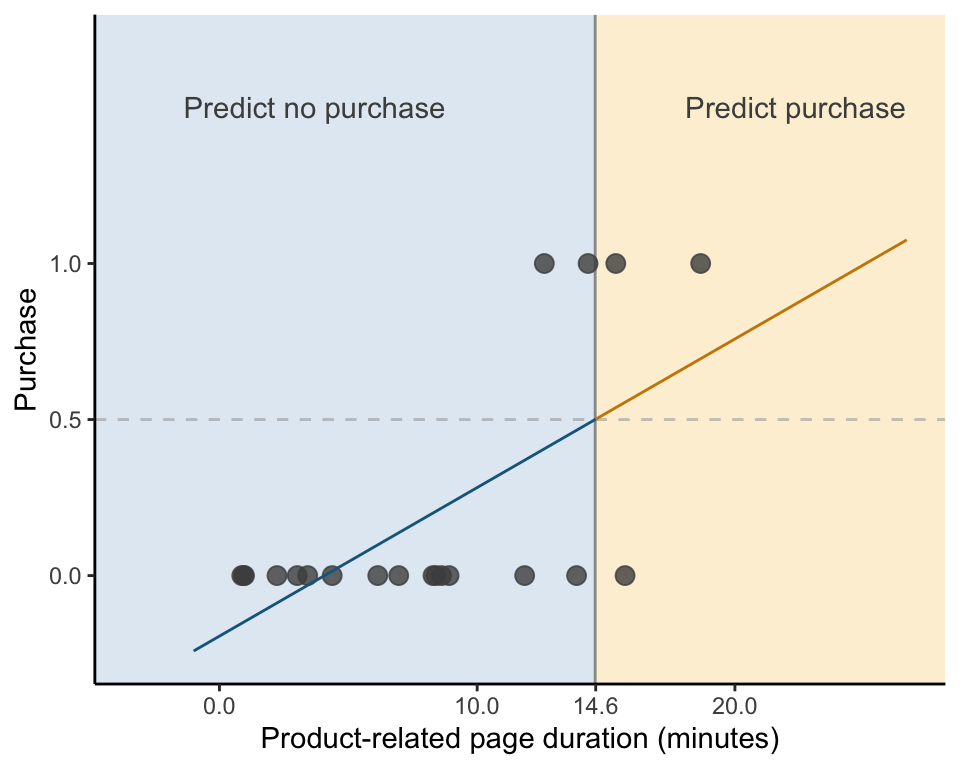
One idea is to convert the non-binary predicted responses to binary values using a thresholding rule. For example, if the LS prediction is greater than 0.5, then we could round the prediction up to 1 (purchase), and if it is less than 0.5, then we could round the prediction down to 0 (no purchase). Figure 11.5 shows the thresholded binary predictions as blue (0) and orange (1). According to our thresholding rule, each session whose product-related page duration exceeds 14.6 minutes (the value that yields the purchase prediction of 0.5) is predicted to make a purchase. Correspondingly, every session whose product-related page duration is less than 14.6 minutes is predicted not to make a purchase.
11.3 Logistic Regression
It is fairly clear that the linear combination LS-based approach that we have presented so far was not designed to predict binary responses. While this doesn’t mean that we can’t use it for binary prediction problems (we’ve just demonstrated that we can!), perhaps we might be able to generate more accurate predictions if we can come up with an approach that is specifically designed for predicting binary responses.
Since linear combinations produce unbounded and continuous predictions, instead of directly predicting the binary response itself, one of the most common approaches to generating linear combination-based predictions of binary responses is to instead predict the probability that the response will equal 1 (because a probability is a continuous value). That is, our initial goal is to compute something like
\[ \textrm{predicted purchase} \textit{ probability} = b_0 + b_1\times \textrm{product-related duration}. \tag{11.1}\]
However, although a probability is a continuous value, it is not unbounded because probabilities always lie between \(0\) (zero chance that the event, such as a purchase, will happen) and \(1\) (absolute certainty that the event, such as a purchase, will happen).4 Since the right side of Equation 11.1 is continuous and unbounded whereas the left side is continuous but bounded between 0 and 1, the two sides of Equation 11.1 are incompatible.
However, to produce a linear combination-based prediction of the binary response probability, we want each side of Equation 11.1 to either both be bounded between 0 or 1 or both be unbounded. Our goal is therefore to create a compatible equation by applying some kind of transformation either (a) to the linear combination (the right side of Equation 11.1) to bound it between 0 and 1 or (b) to the probability (the left side of Equation 11.1) to make it unbounded.
The most common such transformation is the logistic transformation, and the algorithm that uses a logistic linear combination to predict the probability of a success is called logistic regression.
11.3.1 Log Odds and the Logistic Function
To define the logistic transformation, we first need to define something called the log odds (also called the log odds ratio), which can be used to transform the left-side of Equation 11.1 to make it unbounded.
The odds (or the odds ratio; Box 11.1) of a success (e.g., a purchase) is defined as the ratio of the probability of a success and the probability of a failure (e.g., no purchase). If the probability of a success is denoted as \(p\), then the probability of a failure is \(1 - p\), and the odds is equal to
\[ \textrm{odds} = \frac{p}{1 - p}. \tag{11.2}\]
For instance, if a session has a 75 percent chance of ending with a purchase, then it necessarily has a 25 percent chance of not ending with a purchase, and so the odds that the session will end with a purchase is
\[\frac{0.75}{0.25} = \frac{3}{1},\]
which is often stated as “3:1” (“the odds are 3-to-1 that the session will end with a purchase”). The odds always lie between 0 and \(\infty\), which means that they are bounded from below by 0. If the odds are less than 1, then a failure is more likely than a success, whereas if the odds are greater than 1, then a success is more likely than a failure.
It is common to transform the odds to make them unbounded by applying a logarithmic transformation to the odds—that is, to compute the log odds (also called the “logit” function of \(p\)):
\[ \textrm{log odds} = \textrm{logit}(p) = \log\left(\frac{p}{1 - p}\right). \tag{11.3}\]
For example, if the probability that a session will end with a purchase is 0.75, then the log odds that the session will end with a purchase is
\[\log\left(\frac{0.75}{0.25}\right) = \log\left(3\right) = 1.1.\]
Since the log of a number less than 1 is negative, the log odds range from \(-\infty\) to \(\infty\), and is therefore continuous and unbounded. A negative log odds implies that a failure is more likely than a success, whereas a positive log odds implies that a success is more likely than a failure.
Applying the log-odds transformation to the purchase probability response on the left side of Equation 11.1, we get:
\[ \log\left(\frac{p}{1 - p}\right) = b_0 + b_1 \times \textrm{product-related duration}, \tag{11.4}\]
where we define \(p\) to be the predicted probability that the session will result in a purchase. Both sides of Equation 11.4 are now continuous and unbounded (and are therefore compatible).
However, rather than using a linear combination to predict the log odds as in Equation 11.4, it is common to invert this log odds transformation in Equation 11.4 by making \(p\) (the probability of a purchase) the subject of the equation:
\[ p = \frac{1}{1 + e^{-(b_0 + b_1 \textrm{product-related duration})}}. \tag{11.5}\]
In this equivalent formulation, rather than being unbounded, both the left and right sides are now bounded between 0 and 1. The right side transformation is called the logistic function (\(\textrm{logistic}(\gamma) = \frac{1}{1 + e^{-\gamma}}\)). The logistic regression algorithm computes reasonable values for the \(b_0\) and \(b_1\) coefficients in Equation 11.5 so it can be used to predict the probability of a success for new data points.
Figure 11.6 shows the logistic regression fit (i.e., in the form of Equation 11.5) based on the product-related duration predictor variable for the small sample of 20 training data points. The \(y\)-position of each position on the curve corresponds to the purchase probability prediction. Note that this curve asymptotes (i.e., levels off) at \(p = 0\) at one end (for shorter product-related page durations) and asymptotes at \(p = 1\) at the other end (for longer product-related page durations), indicating that the predictions are bounded between 0 and 1. This S-shaped curve that asymptotes at 0 and 1 at either end is typical of a logistic regression fit. The particular formula for this logistic regression fit is given by
\[ \textrm{predicted purchase probability} = \frac{1}{1 + e^{-(-8.639 + 0.613 \textrm{product-related duration})}}. \tag{11.6}\]
We will explain how the \(b_0\) and \(b_1\) coefficients for logistic regression are computed in Section 11.3.3.

11.3.2 Generating Binary Response Predictions for Logistic Regression
Generating predictions using a logistic regression fit is much the same as for a standard linear fit: find the relevant product-related page duration position on the \(x\)-axis and trace your finger up to the corresponding \(y\)-position on the curve to get the predicted probability of the session ending with a purchase. This is equivalent to plugging in the predictor value into the logistic regression fit equation. For example, for the logistic regression fit in Equation 11.6, which is shown in Figure 11.6, the predicted purchase intent probability for a session that spent 20 minutes on product-related pages is 0.97.
However, despite all this work to predict the probability of a success (the probability that the binary response equals 1), in practice, we often want our response prediction to be a binary value (rather than a probability). Fortunately, a response probability prediction can be easily converted to a binary response prediction using a thresholding rule, such as
Predict “1” (that the session will end with a purchase) if the predicted success probability, \(p\), is 0.5 or higher.
Predict “0” (that the session will not end with a purchase) if the predicted success probability, \(p\), is lower than 0.5.
While using a cutoff of 0.5 is very intuitive (i.e., predict that the observation’s response will be 1 if the predicted probability of a success is higher than the predicted probability of a failure), in practice, it often turns out that a different threshold value will generate more accurate predictions when the two classes are not balanced (i.e., when the two classes have differing numbers of observations). We will discuss how to choose a more appropriate threshold in Section 11.4.5.
Note that while we can use a similar thresholding rule for the LS predictions that we produced in Section 11.2, these LS predictions, though continuous, should not be interpreted as a class probability prediction since they are not bounded between 0 and 1.
11.3.3 Fitting Logistic Regression Coefficients
Now that we understand the format of the logistic regression predictions (Equation 11.5), how do we compute the logistic regression coefficients \(b_0\) and \(b_1\)? Recall that for the LS algorithm, we chose the values of \(b_0\) and \(b_1\) such that the predicted responses were as close as possible to the observed responses. If we try to compute the logistic regression \(b_0\) and \(b_1\) coefficients using the same approach, then we will need to find the values of \(b_0\) and \(b_1\) such that the predicted response probabilities are as close as possible to the observed response probabilities.
Sounds simple, right? However, if you put your critical thinking hat on, you will quickly arrive at the problem with this approach: we never actually know the purchase response probability for any individual session.
Imagine that each session has an underlying probability of whether it will end with a purchase. Then sessions with a higher purchase probability are more likely to end in a purchase than sessions with a lower purchase probability. However, we don’t know what a session’s purchase probability is. What we do know is whether the session actually resulted in a purchase. How can we use the observed binary purchase information to compute reasonable values of \(b_0\) and \(b_1\) in the logistic formulation of the purchase probability in Equation 11.5?
11.3.3.1 The Logistic Loss Function
To come up with a meaningful loss function for logistic regression, let’s first ask what constitutes a “good” probability prediction. Ideally, we want a loss function that will be small when the predicted probabilities for sessions that ended with a purchase (i.e., the observations in the “positive” class) are close to 1 and the predicted probabilities for sessions that did not end with a purchase (i.e., the observations in the “negative” class) are close to 0.
One loss function that satisfies this requirement involves computing \(-\log p_i\) for positive class observations and \(-\log(1 - p_i)\) for negative class observations (where \(p_i = \frac{1}{1 + e^{-(b_0 + b_1x_{i})}}\) is the predicted response probability for the \(i\)th observation). The corresponding logistic loss function, which adds up the loss for each training set observation, is given by
\[ \sum_{i \textrm{ in pos class}} (-\log p_i)~ + \sum_{i \textrm{ in neg class}} (-\log(1 - p_i)). \tag{11.7}\]
Our goal is thus to find some values of our coefficients \(b_0\) and \(b_1\) (where we substitute \(p_i = \frac{1}{1 + e^{-(b_0 + b_1x_{i})}}\) in Equation 11.7), such that the logistic loss function is as small as possible.
Without going into the specifics of how this particular format of the loss function was chosen, this loss function corresponds to the negative of a quantity called the “log likelihood,” and it uses the logarithmic transformation primarily so the resulting calculus-based optimization computations are easier to work with. This is an example of a Maximum Likelihood Estimation (MLE) problem (the details of which are not covered in this book).
Unfortunately, as was the case for the least absolute deviation (LAD) and lasso algorithms, there is no neat algebraic formula for the optimal coefficient values that minimize this logistic loss function.5 Instead, approximately optimal values of \(b_0\) and \(b_1\) are typically chosen using a technique called iteratively reweighted least squares (IWLS). The specific details of the IWLS algorithm are unfortunately beyond the scope of this chapter, but you can train the logistic regression algorithm via IWLS using the glm() function in R (specifying the family = "binomial" argument in the glm() function will implement logistic regression). In Python, you can use the linear_model.LogisticRegression() class from the scikit-learn library.
Note that logistic regression is just one example of a class of predictive models known as generalized linear models (GLMs) (Dobson and Barnett 2018), which can be used to compute predictions for a broad range of response types.
11.3.4 Logistic Regression with Multiple Predictive Features
Just as with standard linear fits, the process of training a logistic regression using multiple predictive features involves adding the other predictive features to the linear combination, such as:
\[\begin{equation*} p = \frac{1}{1 + e^{-(b_0 ~+~ b_1 \textrm{product-related duration} ~+~ b_2 \textrm{exit rates} ~+~ b_3 \textrm{returning visitor} + ...)}}. \end{equation*}\]
Note that categorical variables need to be converted to a numeric format or to one-hot encoded (dummy) variables to be included in a logistic regression fit (although, like the lm() function for LS, the glm() function will automatically convert categorical variables to one-hot encoded dummy variables “under the hood”). Similarly, rows with missing values will be automatically dropped from most implementations of logistic regression (so we recommend addressing them yourself during preprocessing before applying the logistic regression algorithm).
To visualize the logistic regression predictions based on multiple predictive features, let’s focus on a fit involving two predictive features: product-related duration and exit rates. Figure 11.7 uses color to indicate the purchase probability predictions for 20 randomly chosen training data sessions, visualized in the space defined by the product-related duration and exit rate predictive features. The color of each point, as well as the background, is based on the predicted probability from the corresponding logistic regression fit. From Figure 11.7, sessions with lower exit rates seem to have a higher predicted probability of resulting in a purchase.
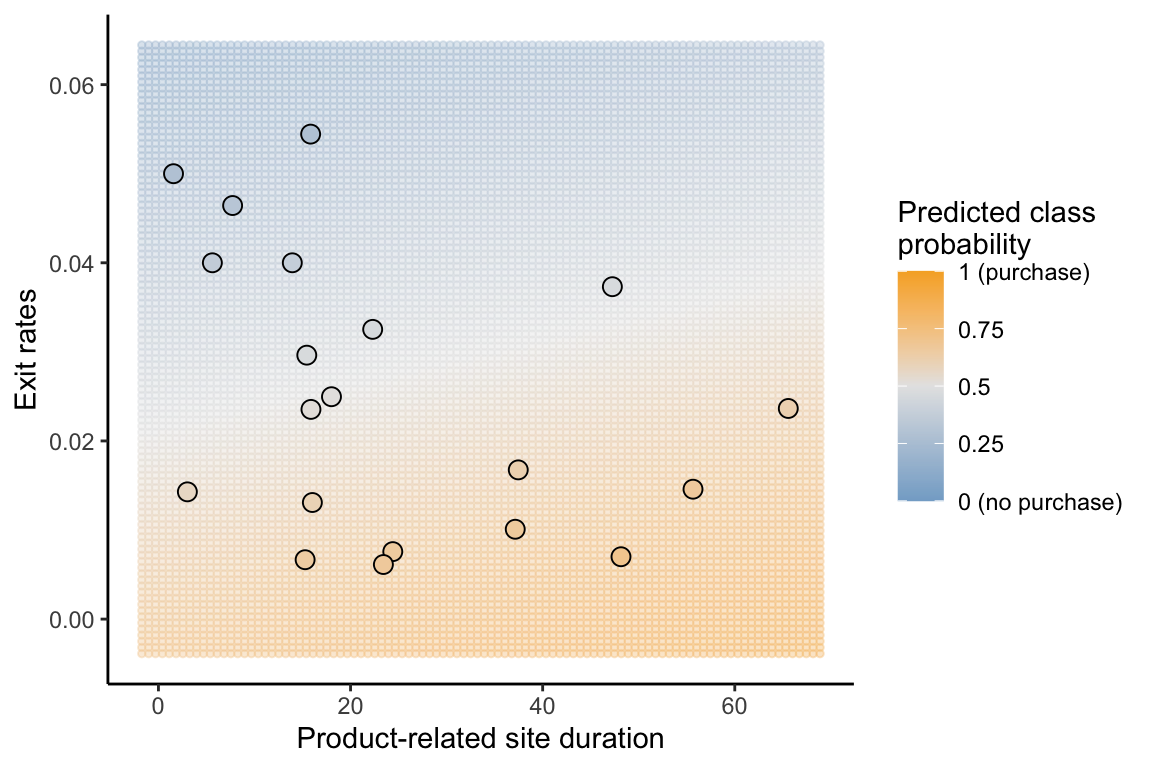
Notice that the “decision boundary” as the probabilities transition from orange (“more likely to result in a purchase”) to blue (“less likely to result in a purchase”) is a straight diagonal line. This is the reason why logistic regression is still considered a linear predictive model, despite the nonlinear transformations involved. To understand why this is the case, an exercise at the end of this chapter will ask you to demonstrate that the decision boundary (the threshold boundary along which the binary prediction switches from 0 to 1) of the logistic regression algorithm is a linear combination of the predictor variables, corresponding to a straight line.
11.3.5 Interpreting and Comparing the Coefficients
How should we interpret the \(b\) coefficients of a logistic regression fit? Recall that the interpretation of the original LS linear fit coefficients is that \(b_1\) is the amount that the predicted response would increase if the value of the first predictive feature increased by 1 unit (without changing the values of the other features).
Based on the log-odds formulation (using the two-predictor fit as an example), where
\[\log\left(\frac{p}{1 - p}\right) = b_0 + b_1 \textrm{product-related duration} + b_2 \textrm{exit rates}, \]
the corresponding interpretation of the logistic coefficients is that \(b_0\) is the “base” predicted log odds of a success (e.g., purchase) occurring for a hypothetical “empty” observation (e.g., a session that spends 0 minutes on product-related pages and has an exit rate value of 0), \(b_1\) corresponds to the amount that the predicted log odds of a purchase will increase if the session spends an additional minute on product-related pages (without changing the value of the exit rate variable), and \(b_2\) corresponds to the amount that the predicted log odds of a purchase will increase if the exit rate value increases by 1 unit (without changing the value of the product-related duration variable).
Similar to the original LS linear fit, if you want to use the coefficients as a measure of feature importance, you will need to either standardize the predictor variables before using logistic regression (although standardization is not required for logistic regression in general) or you will need to standardize the coefficients themselves; for instance, using the bootstrapping (sampling with replacement) technique from Section 10.1.2 in Chapter 10.
Table 11.2 shows the original coefficient value, the corresponding bootstrapped standard deviation (SD), and the bootstrap-standardized coefficient value for the 10 variables with the largest standardized coefficients for a logistic regression fit trained on the default version of the full cleaned/preprocessed training dataset.
| Variable | Coefficient | Estimated (bootstrapped) SD | Standardized coefficient |
|---|---|---|---|
| page values | 0.082 | 0.006 | 13.51 |
| exit rates | -14.864 | 2.727 | -5.45 |
| traffic type 8 | 0.789 | 0.226 | 3.49 |
| month Dec | -0.838 | 0.256 | -3.28 |
| month Mar | -0.646 | 0.234 | -2.76 |
| month May | -0.619 | 0.226 | -2.74 |
| traffic type 10 | 0.398 | 0.198 | 2.00 |
| traffic type 3 | -0.325 | 0.165 | -1.97 |
| month Nov | 0.412 | 0.224 | 1.84 |
| traffic type 2 | 0.225 | 0.123 | 1.83 |
Notice that the most important feature is the “page values,” followed by “exit rates,” the “traffic type 8” one-hot encoded dummy variable, and the “month Dec” one-hot encoded dummy variable. The fact that the “page values” variable is the most important feature is not surprising if you recall its definition (from Section 11.1.1) as a measure of how much each of the pages visited during the session contributes to the site’s revenue.
11.4 Quantitative Measures of Binary Predictive Performance
Now that we know how to generate binary response probability predictions using logistic regression, we need to develop some performance measures for evaluating them.
In this section, we will be evaluating versions of the LS and logistic regression algorithms that have been trained using all 53 predictive features and all 7,372 user sessions from our default cleaned and preprocessed version of the training data (in which we convert categorical variables to one-hot encoded dummy variables, do not log-transform any of our predictors, and do not remove extreme variables, etc.).
Recall that to demonstrate the predictability of these algorithms, they need to be evaluated using future/external data or a surrogate for future/external data, such as the validation set. However, for demonstration purposes, we will first use a random sample of just 20 validation set sessions. Table 11.3 shows the observed response for the 20 sessions, along with the LS and logistic regression purchase response predictions (the binary predictions are shown in parentheses, based on a prediction threshold of 0.5).
Note that since we don’t know the “true” response probabilities, we typically evaluate the (thresholded) binary response predictions, rather than the response probability predictions themselves.
| Observed purchase response | LS predicted (binary) purchase response | Logistic regression predicted (binary) purchase response |
|---|---|---|
| 1 | 0.34 (0) | 0.35 (0) |
| 1 | 0.33 (0) | 0.42 (0) |
| 1 | 0.62 (1) | 0.89 (1) |
| 1 | 0.43 (0) | 0.66 (1) |
| 1 | 0.42 (0) | 0.59 (1) |
| 0 | 0.08 (0) | 0.04 (0) |
| 0 | 0.35 (0) | 0.4 (0) |
| 0 | 0.06 (0) | 0.04 (0) |
| 0 | 0.05 (0) | 0.04 (0) |
| 0 | 0.08 (0) | 0.06 (0) |
| 0 | 0.06 (0) | 0.04 (0) |
| 0 | 0.19 (0) | 0.18 (0) |
| 0 | 0.24 (0) | 0.22 (0) |
| 0 | 0.09 (0) | 0.06 (0) |
| 0 | 0.13 (0) | 0.1 (0) |
| 0 | 0.43 (0) | 0.58 (1) |
| 0 | 0.38 (0) | 0.45 (0) |
| 0 | 0.32 (0) | 0.36 (0) |
| 0 | 0.5 (1) | 0.76 (1) |
| 0 | 0.39 (0) | 0.54 (1) |
11.4.1 Prediction Accuracy and Prediction Error
From Table 11.3, notice that both the LS and logistic regression predictions are correct (i.e., the predicted binary response matches the observed response) for 15 of the 20 validation set sessions (75 percent). An equivalent way to look at this performance would be to consider that each algorithm incorrectly predicted the purchase intent of 5 validation sessions (25 percent).6
The proportion of observations whose binary response is correctly predicted is called the prediction accuracy (box 11.5), and the proportion of observations whose binary response is incorrectly predicted is called the prediction error (Box 11.5). If we have \(n\) data points that we are using for evaluation, then the prediction accuracy is defined as
\[ \textrm{prediction accuracy} = \frac{\left(\textrm{number of correct predictions}\right)}{n}, \tag{11.8}\]
and the prediction error is defined as
\[ \textrm{prediction error} = \frac{\left(\textrm{number of incorrect predictions}\right)}{n}. \tag{11.9}\]
Note that the prediction accuracy and the prediction error together should add up to 1, so
\[ \textrm{prediction error} = 1 - \textrm{prediction accuracy}. \tag{11.10}\]
When the prediction accuracy and the prediction error are computed on the training data, they are called the training accuracy and training error, respectively. However, since training error and training accuracy aren’t particularly good indications of how well our algorithm will be able to predict the responses for external or future data, it is a good idea to also compute the prediction accuracy/error on external/future data or validation data. Recall that evaluating algorithms using the validation set is an excellent way of demonstrating predictability.
11.4.2 The Confusion Matrix
A common way to present the results of a predictive algorithm is to cross-tabulate the observed response labels with the predicted response labels in a 2-by-2 table called the confusion matrix (Figure 11.8). Despite its name, the confusion matrix is not designed to confuse you; instead, it is designed to demonstrate the extent to which the predictive algorithm is confused.
The format of the confusion matrix is shown in Figure 11.8, where one class is denoted as the “positive” class (usually chosen as the class you care more about, but this choice is fairly arbitrary), and the other as the “negative” class.7 For the online purchase data, we choose the “purchase” class to be the positive class, which means that the “no purchase” class will be the negative class.

The confusion matrix tabulates the number of the following:
True positive: A positive class observation that is correctly predicted to be in the positive class
False positive: A negative class observation that is incorrectly predicted to be in the positive class
True negative: A negative class observation that is correctly predicted to be in the negative class
False negative: A positive class observation that is incorrectly predicted to be in the negative class
For the set of 20 validation set sessions, the confusion matrices for the logistic regression and LS fits are given in Table 11.4 and Table 11.5, respectively.
| Predicted purchase | Predicted no purchase | |
|---|---|---|
| Observed purchase | 3 | 2 |
| Observed no purchase | 3 | 12 |
| Predicted purchase | Predicted no purchase | |
|---|---|---|
| Observed purchase | 1 | 4 |
| Observed no purchase | 1 | 14 |
As an exercise, re-create these confusion matrices yourself based on the predictions in Table 11.3.
Since the diagonal entries of the confusion matrix correspond to the sessions with correctly predicted purchase intent (and the off-diagonal entries are the sessions with incorrectly predicted purchase intent), ideally, you will see larger numbers in the diagonal cells (top-left and bottom-right) and smaller numbers in the off-diagonal cells (top-right and bottom-left).
Why is the confusion matrix helpful? It turns out that many of the common binary response prediction performance measures can be computed directly from the confusion matrix. For instance, the prediction accuracy can be calculated directly from the confusion matrix by adding the numbers in the diagonal cells and dividing that sum by the sum of all the numbers in the matrix. From the confusion matrix for the 20 sample validation set sessions in Table 11.4, the logistic regression prediction accuracy is \((3 + 12) / 20 = 0.75\), which is the same as the LS prediction accuracy, \((1 + 14) / 20 = 0.75\).
While prediction accuracy is a very important metric, it doesn’t always provide a complete picture of predictive performance. As an example, consider the fact that a predictive algorithm that always predicts the binary response to be in the positive class will have an accuracy equal to the proportion of the observations that are in the positive class. So if 90 percent of the observations being evaluated are in the positive class, then such an algorithm will be 90 percent accurate, which sounds pretty good! However, looking at the predictive performance of the positive and negative classes separately paints a very different picture. For an algorithm that always predicts a positive response, if we restricted the accuracy calculation to just the positive class observations, it would have an accuracy of 100 percent (which is amazing!), but if we restricted the accuracy calculation to just the negative class observations, it would have an accuracy of 0 percent (which is terrible!). Fortunately, some additional predictive performance measures can help paint a more complete picture of the prediction performance of your algorithm.
11.4.3 True Positive Rate
The true positive rate (Box 11.7) corresponds to the proportion of the sessions in the positive class (i.e., sessions that ended with a purchase) whose binary response is correctly predicted:
\[ \begin{align} \textrm{true positive rate} &= \frac{\left(\textrm{number of correctly predicted positive class obs}\right)}{(\textrm{number of positive class observations})} \nonumber\\ & = \frac{\left(\textrm{number of true positives}\right)}{(\textrm{number of positive class observations})} \end{align} \tag{11.11}\]
The true positive rate is often called the sensitivity (“How sensitive is the algorithm to detecting the positive class?”) or the recall (“How many of the positive class observations did the algorithm recall?”). The true positive rate/sensitivity/recall gives us an idea of how good our algorithm is specifically at identifying the sessions that actually ended in a purchase (ignoring the predictions for the sessions that did not end with a purchase).
The calculation of the true positive rate using the confusion matrix involves dividing the number of correctly classified positive observations (the top-left cell) by the total number of positive class observations (the sum of the top row). Based on the confusion matrix in Table 11.4, the true positive rate/sensitivity/recall for the logistic regression predictions for the sample of 20 validation set sessions is \(3 / (3 + 2) = 0.6\). That is, 60 percent of the positive class observations (sessions with a purchase) are correctly predicted to result in a purchase by the logistic regression algorithm. Similarly for the confusion matrix in Table 11.5, the true positive rate/sensitivity/recall for the LS predictions for the sample of 20 validation set sessions is \(1 / (1 + 4) = 0.2\). That is, only 20 percent of the positive class observations (sessions with a purchase) are correctly predicted to result in a purchase by the LS algorithm. (We will calculate the true positive rates for the full validation set when we conduct a predictability assessment in Section 11.5.1.)
In the same way that the error is the converse of the accuracy, the converse of the true positive rate is the false negative rate, which corresponds to the proportion of positive sessions (i.e., those that actually ended in a purchase) whose class is incorrectly predicted to be negative:
\[\textrm{false negative rate} = 1 - \textrm{true positive rate}.\]
11.4.4 True Negative Rate
The true negative rate (Box 11.8) corresponds to the proportion of negative class sessions (i.e., those that did not end with a purchase) whose response/class is correctly predicted. The true negative rate is often called the specificity.
Calculating the true negative rate involves dividing the number of correctly classified negative class observations (the bottom-right cell in the confusion matrix) by the total number of negative observations (the sum of the bottom row of the confusion matrix).
Based on the confusion matrix in Table 11.4, for the sample of 20 validation set sessions whose response has been predicted using the logistic regression algorithm, the estimated true negative rate is \(12 / (3 + 12) = 0.8\). That is, 80 percent of the negative class observations (sessions without a purchase) are correctly predicted not to result in a purchase by the logistic regression algorithm. Correspondingly, for the confusion matrix in Table 11.5 for the LS algorithm, the estimated true negative rate is \(14 / (1 + 14) = 0.93\). That is, 93 percent of the negative class observations (sessions without a purchase) are correctly predicted not to result in a purchase by the LS algorithm. (We will calculate the true negative rates for the full validation set when we conduct a predictability assessment in Section 11.5.1.)
The converse of the true negative rate is the false positive rate, which corresponds to the proportion of negative sessions (i.e., those that did not end in a purchase) whose class is incorrectly predicted to be positive, and is given by:
\[\textrm{false positive rate} = 1 - \textrm{true negative rate}.\]
11.4.5 The Sensitivity-Specificity Trade-Off: Choosing the Binary Threshold Value
For the 20-validation set sessions, the true positive rate (60 percent) for the logistic regression algorithm is a lot lower than the true negative rate (80 percent). That is, our algorithm was a lot better at correctly identifying when a session is not going to result in a purchase than identifying when a session is going to result in a purchase. If you care more about correctly identifying the purchase intent of sessions that will not result in a purchase, then this is fine; but if instead, you care more about correctly identifying the purchase intent of sessions that will result in a purchase, this is not a particularly desirable trait.
There are some domain problems where you will have a preference either for optimal specificity (true negative) or sensitivity (true positive) performance. For example, in the context of medical diagnosis problems, high false negative rates (low true positive rates) can mean that deadly diagnoses are missed more often, whereas high false positive rates (low true negative rates) can mean that patients are incorrectly diagnosed with diseases more often. Unfortunately, there is often a trade-off between these two performance measures: higher true positive rates often mean lower true negative rates and vice versa. For medical diagnosis examples, the more severe the disease, the more you may want to prioritize having a higher true positive rate (to ensure that you miss as few diagnoses as possible), even if it is at the cost of a slightly lower true negative rate.
There is a parameter that is built into our binary prediction algorithms that can be used to tweak the trade-off between the true positive and the true negative rates. This parameter is the probability prediction threshold, which we had set to 0.5 earlier (up until now, a probability prediction above 0.5 was converted to a positive prediction, while a probability prediction below 0.5 was converted to a negative prediction).
Increasing the threshold value means that more of our predictions will be negative and fewer will be positive, which typically increases the true negative rate and decreases the true positive rate. Conversely, decreasing the threshold value tends to decrease the true negative rate and increase the true positive rate.
To visualize this dial, Figure 11.9 shows the distribution of the logistic regression predicted probability of a purchase for the sessions that did (orange) and did not (blue) result in a purchase, based on the 20 validation set sessions. Density plots are an excellent way to visualize the predictive performance of any binary prediction algorithm that outputs class probability predictions. Ideally, the peak of the predicted response probability distribution for positive class sessions will be much higher than the peak of the distribution for the negative class predicted response probabilities, with minimal overlap between the densities of the two classes. Is this what you see in Figure 11.9? The negative class peak is certainly much lower than the positive class peak, but there is quite a lot of overlap between the two densities.

If we want to increase our true positive rate (i.e., do a better job of correctly predicting the purchase intent of the sessions that actually do result in a purchase), we could lower the probability prediction threshold from 0.5 to, say, 0.3 (i.e., predict that a session will end in a purchase if the predicted purchase probability/response is greater than 0.3, rather than 0.5).
There are many ways to choose the threshold value. One idea is to tune the value of the threshold value, for example, using cross-validation (CV). However, recall that to tune a parameter, you need to have a measure that you’re trying to optimize. For prediction problems, many people will simply try to optimize the prediction accuracy, but as we’ve seen, prediction accuracy doesn’t always paint the entire picture. Similarly, if you were to try to optimize the true positive rate, you would be doing so at the cost of the true negative rate, and vice versa. Ideally, you will try to optimize all these performance measures at once (e.g., find a value of the threshold that simultaneously yields reasonable CV accuracy, as well as CV true positive and true negative rates).
An alternative (and much simpler) approach that is surprisingly effective is to set the threshold to be the proportion of observations that are in the positive class in the training data, which in our online shopping training dataset is 0.161. While this might not look like a great choice for our sample of 20 validation sets, we will see that this is a good choice when we evaluate each algorithm using the full validation set during our predictability analysis in Section 11.5.1.
11.4.6 ROC Curves
Although there is a trade-off between true positive and true negative rates, this trade-off is not infinitely flexible. There is an upper bound for the overall predictive performance potential that is specific to each particular algorithm and dataset. For instance, for one algorithm, you may be able to tune the results such that the true positive and true negative rates are both around 0.8, whereas for another algorithm that has lower predictive performance potential overall, if you achieved a true positive rate of 0.8, you might be able to get a true negative rate of only around 0.6.
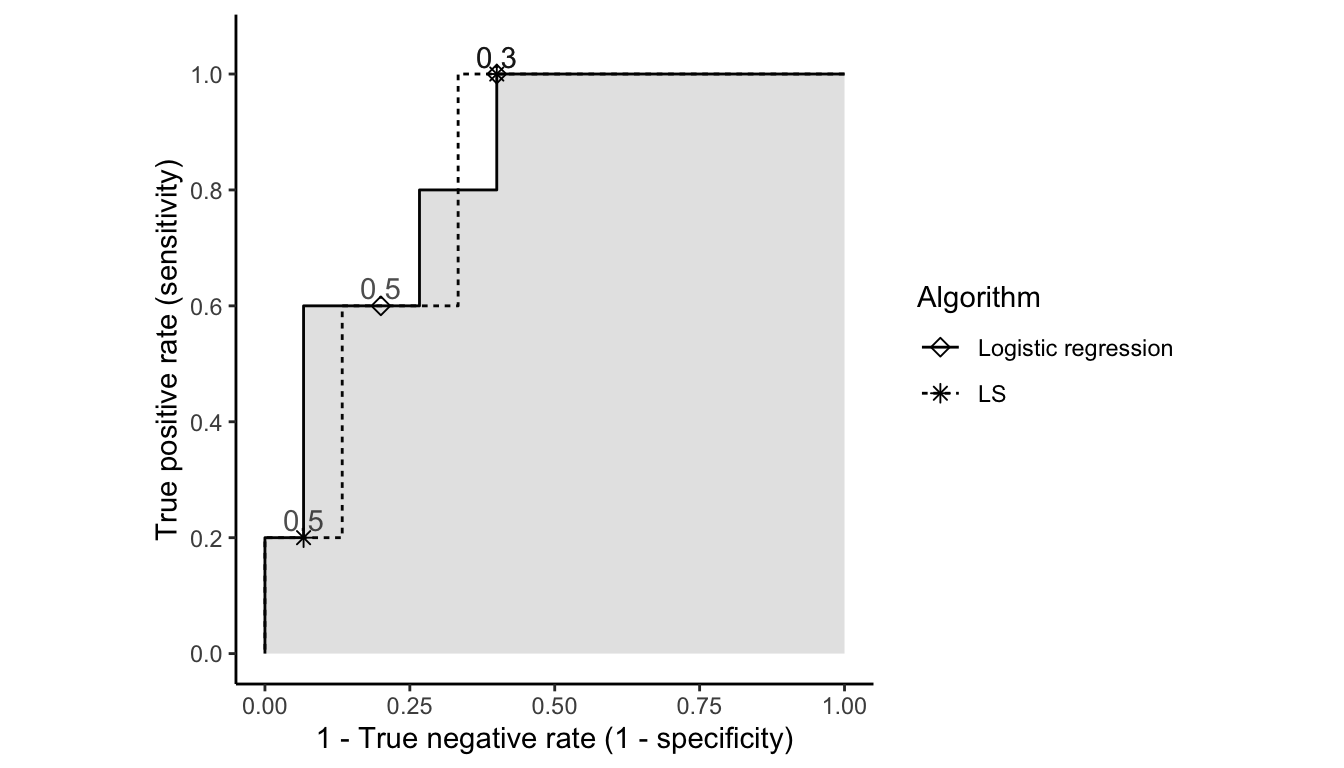
One common way to visualize the overall predictive potential of an algorithm across a range of different thresholds is to plot the true positive rate and true negative rates that are achieved for a variety of thresholds. For instance, Figure 11.10 displays the true positive rate and \(1 -\) true negative rate values for the logistic regression algorithm using two thresholds: 0.3 and 0.5, where each rate is computed based just on our sample of 20 validation set sessions.

A point in the top-left corner of this plot (where the true positive rate and true negative rate both equal 1) would correspond to an algorithm with perfect predictions, so the closer the point is to the top-left corner, the better the overall predictive performance. In contrast, points falling on the dotted diagonal line correspond to the performance that you get when you randomly guess the class for each point (such that the probability of guessing each class equals the proportion of observations that are in the class). Thus, anything above the diagonal is a classifier that is better than a random guess, and anything below it is worse.
Of the two points in Figure 11.10, which do you think is exhibiting better performance? The answer to this question will depend on whether you value having a higher true positive rate or a higher true negative rate. The threshold of 0.3 has a higher true positive rate than the threshold of 0.5, but it also has a lower true negative rate. Whether the increase in the true positive rate is worth the slight decrease in the true negative rate is a matter of opinion that should be based on the specific problem being solved.
While looking at the predictive performance for individual threshold choices can be informative, it is common to simultaneously visualize the true positive and true negative rates across the entire range of thresholds by creating a receiver operating characteristics (ROC) curve (Box 11.10). An ROC curve involves plotting a line that connects the true positive and true negative rate coordinates across all threshold values (ranging from 0 to 1). ROC curves can be useful both for choosing the threshold by visualizing the trade-off between the true positive and true negative rates, as well as for comparing the overall predictive potential of multiple algorithms. When computed based on the same set of data points, the algorithm whose ROC curve sits above (i.e., closer to the top-left of the plot) the other is the one that has greater overall predictive potential (although there may still be individual choices of threshold values for which the other algorithm is preferable).
Figure 11.11 plots the ROC curves for the logistic regression (darker solid) and LS (lighter dashed) predictions, both evaluated using the 20 validation set sessions. Overall, the two algorithms are very similar, but the logistic regression algorithm has slightly better predictive potential, as quantified by the area under the curve (AUC). The AUC quantifies the aggregate predictive potential across all thresholds for the algorithm by computing the literal area under the ROC curve. The highest possible AUC is 1 (if the area under the curve takes up the entire space). In Figure 11.11, the logistic regression algorithm has a slightly higher AUC (0.84) than the LS algorithm (0.813) based on this sample of 20 validation set sessions. An AUC of above 0.8 is considered fairly good, but it depends on the domain (there are some medical problems, where only an AUC above 0.95 is considered acceptable).
11.4.7 Class Imbalance
For prediction problems where the data has a class imbalance (i.e., there are a lot more training data points in one class than another), most algorithms will tend to overpredict the majority class (the class with more observations in it). For the online purchase problem, there are a lot more sessions that don’t end with a purchase than sessions that do, and thus most algorithms that we train will tend to be more likely to predict that new sessions won’t end in a purchase.
Our preferred method of addressing class imbalance is to tweak the probability threshold, setting it equal to the proportion of observations in the positive class, as discussed in Box 11.9. This will typically lead to better prediction performance than a threshold of 0.5 for problems with class imbalance.
Other ways of dealing with class imbalance include downsampling the majority class (Kubat and Matwin 1997), upsampling the minority class, and the Synthetic Minority Oversampling Technique (SMOTE) (Chawla et al. 2002). There is, however, much debate about the effectiveness of these techniques in practice.
11.5 PCS Scrutinization of Binary Prediction Results
So far, we have only trained our LS and logistic regression binary predictive algorithms using one possible version of the cleaned and preprocessed data (our default version), and we have evaluated them using just a sample of 20 validation set sessions.
In this section, we will conduct a predictability, computability, and stability (PCS) evaluation of LS and logistic regression predictive algorithms by first evaluating the predictability of our predictive fits using the entire validation set (rather than just the set of 20 randomly chosen validation sessions). Next, we will investigate various sources of uncertainty associated with our predictions by examining the stability of these fits based on how their performance changes when they are trained on perturbed versions of the data designed to emulate alternative datasets that may have arisen from the data collection mechanism, as well as on alternative cleaned and preprocessed versions of the data based on different cleaning/preprocessing judgment calls.
Because 16.1 percent of the training data sessions ended with a purchase, we will be using the binary probability prediction threshold of 0.161 to convert our predictions to binary response predictions in our analyses that follow (i.e., we will predict that the session will end in a purchase if the predicted probability of the session ending in a purchase is at least 0.161). Note that although the LS-based continuous predictions of the binary responses should not be interpreted as probability predictions, we will still use the threshold of 0.161 to convert them to binary values (since we find that this works fairly well in practice).
The code and documentation for the assessments that we conduct in this section can be found in the 03_prediction_logistic.qmd (or .ipynb) file in the online_shopping/dslc_documentation/ subfolder of the online GitHub repository.
11.5.1 Predictability
Table 11.6 and Table 11.7 give the confusion matrices for the LS and logistic regression algorithms trained on the default version of the cleaned/preprocessed training data and evaluated on the full corresponding validation dataset (rather than just the randomly selected sample of 20 validation sessions).
| Predicted purchase | Predicted no purchase | |
|---|---|---|
| Observed purchase | 321 | 41 |
| Observed no purchase | 524 | 1570 |
| Predicted purchase | Predicted no purchase | |
|---|---|---|
| Observed purchase | 287 | 75 |
| Observed no purchase | 365 | 1729 |
Can you compute an estimate of the prediction accuracy using these validation set confusion matrices for the LS and logistic regression algorithms? You should find that the LS algorithm has a validation set accuracy of 0.77, while the logistic regression algorithm has an accuracy of 0.82. Since these evaluations are conducted for the validation set, this provides reasonable evidence of the predictability of the algorithm, but recall that we shouldn’t rely on prediction accuracy alone.
Table 11.8 shows the accuracy, true positive rate, true negative rate, and AUC of each algorithm. Note that (using the probability prediction threshold of 0.161) the logistic regression algorithm has a higher true negative rate than the LS algorithm, but a lower true positive rate.
| Fit | Accuracy | True pos. rate | True neg. rate | AUC |
|---|---|---|---|---|
| Logistic regression | 0.821 | 0.793 | 0.826 | 0.898 |
| LS | 0.770 | 0.887 | 0.750 | 0.905 |
What is particularly surprising, however, is that the LS algorithm (which was not designed for binary responses) has a slightly higher AUC than the logistic regression algorithm (which was designed for binary responses). This means that (for this problem, at least) the LS algorithm actually has slightly higher predictive performance potential when viewed across all threshold values than the logistic regression algorithm (however, this improvement is very small and the two algorithms have very similar predictive performance overall). Figure 11.12 shows the ROC curve for the LS and logistic regression algorithms, in which the LS ROC curve indeed sits slightly above the logistic regression ROC curve.
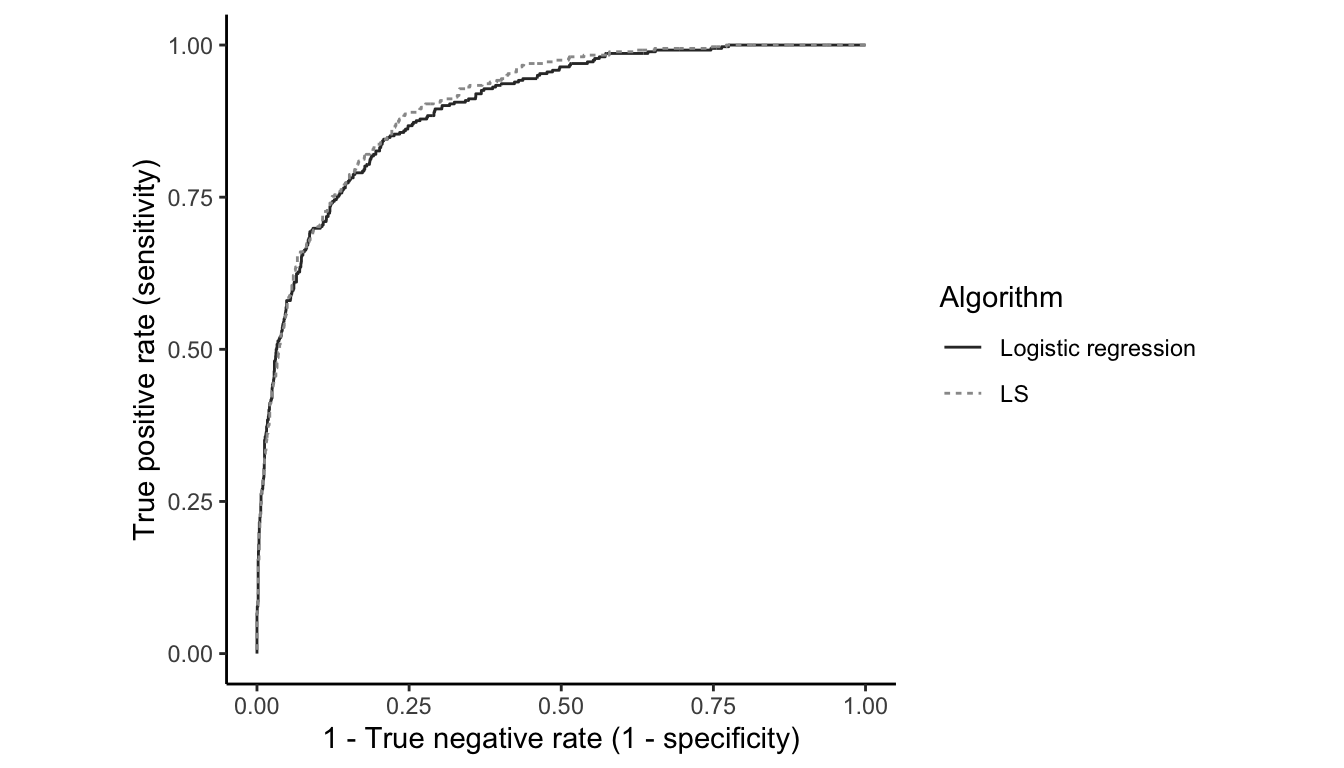
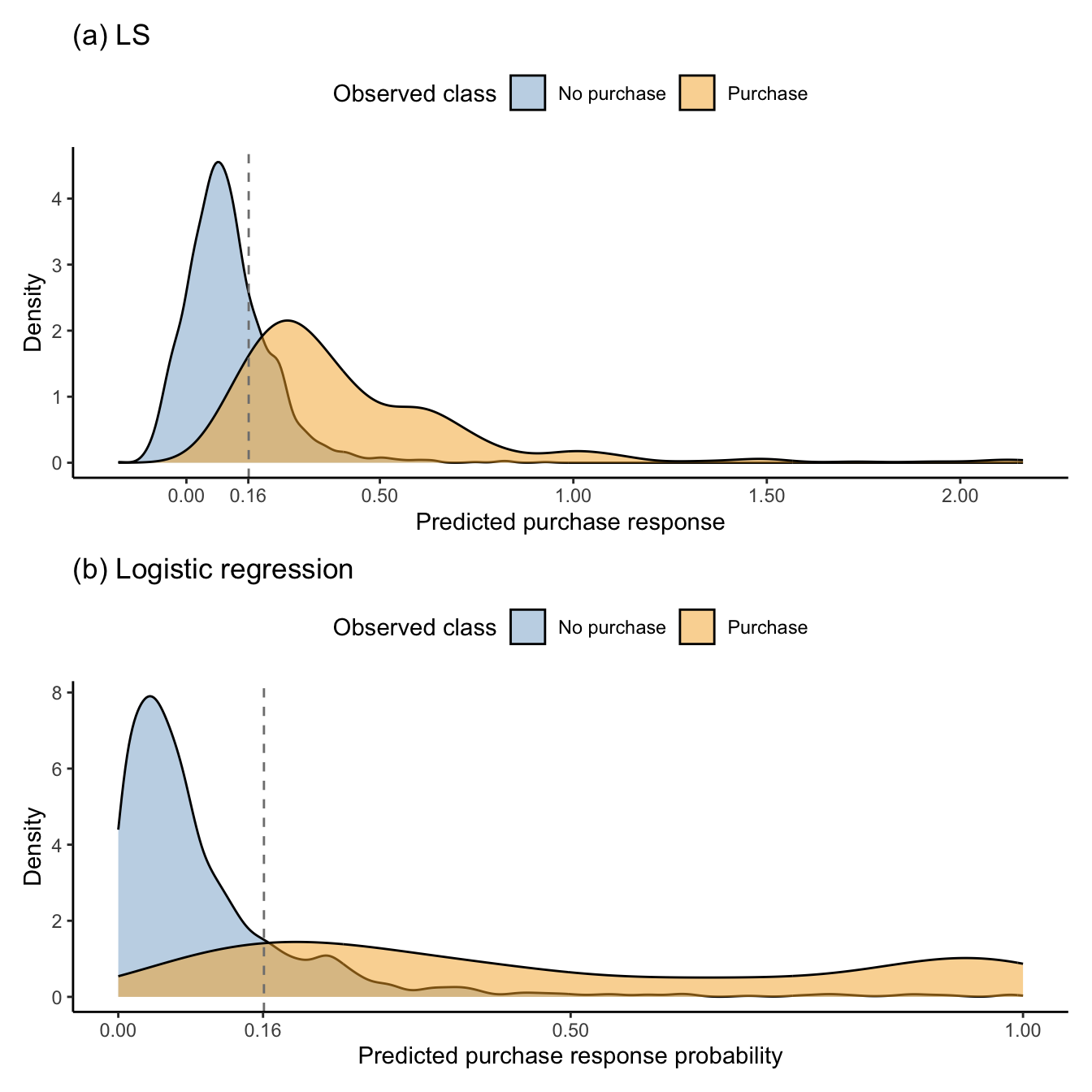
Figure 11.13 shows the distribution of the unthresholded LS and logistic regression validation set predictions for each class (purchase and no purchase), with the threshold of 0.161 annotated. This threshold choice seems to be a good choice for the logistic regression algorithm, but a slightly higher threshold may actually be better for the LS algorithm. Note in Figure 11.13(b) that the logistic regression probability predictions have a clear low-probability peak for the “no purchase” class (i.e., the sessions that did not end in a purchase primarily have low purchase intent probability predictions), but the probability predictions for the “purchase” class are spread fairly evenly throughout the probability space (i.e., sessions that ended with a purchase do not primarily have high purchase intent probabilities). This means that the algorithm is doing a good job of detecting when a session is unlikely to end with a purchase, but it is not doing a good job of identifying when a session is likely to end with a purchase.
11.5.2 Stability
Next, let’s investigate the stability of our predictive algorithms. As in previous chapters, we will first explore the uncertainty arising from the data collection process by evaluating the stability of our predictive fits to plausible data perturbations. We will then explore the uncertainty arising from the data cleaning and preprocessing steps by evaluating the stability of our predictive fits to reasonable alternative cleaning/preprocessing judgment calls. By comparing the LS and logistic regression algorithms, these evaluations also assess the stability of our predictive fits to the choice of algorithm.
11.5.2.1 Stability to Data Perturbations
In this section, we will explore the uncertainty arising from the data collection procedure by investigating how our predictive performance changes when we perturb our training data (e.g., by adding random noise or performing bootstrapping) in a way that is designed to emulate alternative datasets that could have been generated by the data collection procedure. In the case of the online shopping data, it seems unlikely that variables such as the number of administrative pages visited or the type of browser being used would contain errors or be imprecise because they would likely have been recorded by an automated system. Therefore, adding random noise to these variables does not seem like a reasonable data perturbation. It is, however, entirely possible that the website could have had a different (but equivalent) set of user sessions, which implies that bootstrapping would be a reasonable data perturbation.
In Figure 11.14, we compare the ROC curves for 10 LS and logistic regression fits, each trained on a different bootstrapped sample of the training data where the predictions are evaluated using the full validation set. The 10 perturbed ROC curves look fairly similar to one another for each algorithm, indicating that the predictive performance of both algorithms is fairly stable to these sampling perturbations.

Next, Figure 11.15 shows the distribution of the true positive rate (sensitivity), true negative rate (specificity), and accuracy metrics for each algorithm, trained this time on 100 bootstrapped versions of the training data (where the evaluations are again based on the validation set). Each algorithm uses a prediction probability threshold based on the proportion of training sessions that ended with a purchase to create the binary response predictions. Based on the widths of the boxplots, the logistic regression algorithm seems to be slightly more stable in terms of the true negative rate and accuracy metrics, but slightly less stable in terms of the true positive rate metric.

Unfortunately, because our observed responses and binary predictions are all equal to 0 or 1, we cannot visualize the stability of the individual binary predictions using a prediction stability plot as we did for our continuous response problem (see Figure 10.10 in Chapter 10). While we could visualize the range of the unthresholded “probability” response predictions (instead of the binary predictions), note that there is no “true” probability response to compare them with.
We can, however, visualize the stability of the coefficients (where, to ensure that the coefficients are comparable, we will first standardize each predictor variable by subtracting the mean and dividing the SD for each column in each bootstrapped training dataset before computing the LS and logistic regression fits).
Figure 11.16 shows the distribution of the coefficients for the top 20 variables (in terms of the largest absolute value logistic regression coefficient across the perturbed fits) for the (a) LS and (b) logistic regression algorithms, each trained on 100 bootstrap-perturbed versions of the default cleaned/preprocessed training dataset. The coefficients for both algorithms seem fairly stable, except for the month_Feb one-hot encoded dummy variable, whose logistic regression coefficient is surprisingly unstable. This indicates that we shouldn’t try to interpret the Feb coefficient with any seriousness and certainly warrants an exploration into why the Feb variable is so unstable, but we will leave this as an activity for the motivated reader.

The fact that the page values, exit rates, and December (dummy variable) features are important (in terms of coefficient magnitude) for both algorithms is additional evidence of the stability of the predictive power of these features for predicting purchase intent.
11.5.2.2 Stability to Data Cleaning and Preprocessing Judgment Calls
Recall from Section 11.1.3 that we made several judgment calls while cleaning and preprocessing the online shopping data. So far, we have investigated only one particular version of the cleaned/preprocessed dataset that is based on the default arguments of our cleaning/preprocessing function (see the 01_cleaning.qmd or .ipynb file in the online_shopping/dslc_documentation/ subfolder of the supplementary GitHub repository for details). However, there are several alternative versions of the cleaned/preprocessed shopping dataset that we could have created if we had made alternative cleaning/preprocessing judgment calls. In this section, we will investigate the stability of our predictive performance to several alternative judgment call combinations.
The judgment calls we will consider are:
Converting the numeric variables (such as
browser,region, andoperating_system) to categorical variables, or leaving them in a numeric format (just in case there is some meaningful order to the levels that we don’t currently know about).Converting the categorical
monthvariable to a numeric format (since there is a natural ordering to the months), or leaving it in a categorical format (which will be turned into one-hot encoded dummy variables during preprocessing).Applying a log-transformation to the page visit and duration variables (because this makes the distributions look more symmetric, and may help improve predictive performance), or leaving them un-transformed.
Removing very extreme sessions (e.g., that visited over 400 product-related pages in a single session, or spent more than 12 hours on product-related pages in a single session) that may be bots, versus leaving them in the data. Note that we chose these thresholds subjectively based on a visualization of the distributions of these variables.
Since each of these judgment calls have two options (true or false), there are a total of \(2^4 = 16\) judgment call combinations that we will consider in this section.
Before evaluating the stability of the LS and logistic regression algorithms to these judgment calls, we conducted predictability screening, where we include only the judgment call combinations that yield a validation set predictive performance that is above a certain threshold (such as an AUC above 0.8). Fortunately, all 16 fits for both algorithms yielded an AUC of greater than 0.895, which feels fairly reasonable, so we did not discard any of them.
Figure 11.17 shows the ROC curves for each of the 16 judgment call-perturbed LS and logistic regression fits. There is very little difference between the 16 ROC curves in each figure, indicating that our results are very stable to these particular cleaning/preprocessing judgment calls. Figure 11.18 presents the distributions of the performance measures across the 16 versions of each algorithm, each evaluated on the validation set using a binary prediction threshold of 0.161. Overall, both algorithms seem to have very stable predictive performance with respect to this particular collection of 16 judgment calls (in the context of this particular problem, errors within a 3-percentage-point window feel fairly stable).
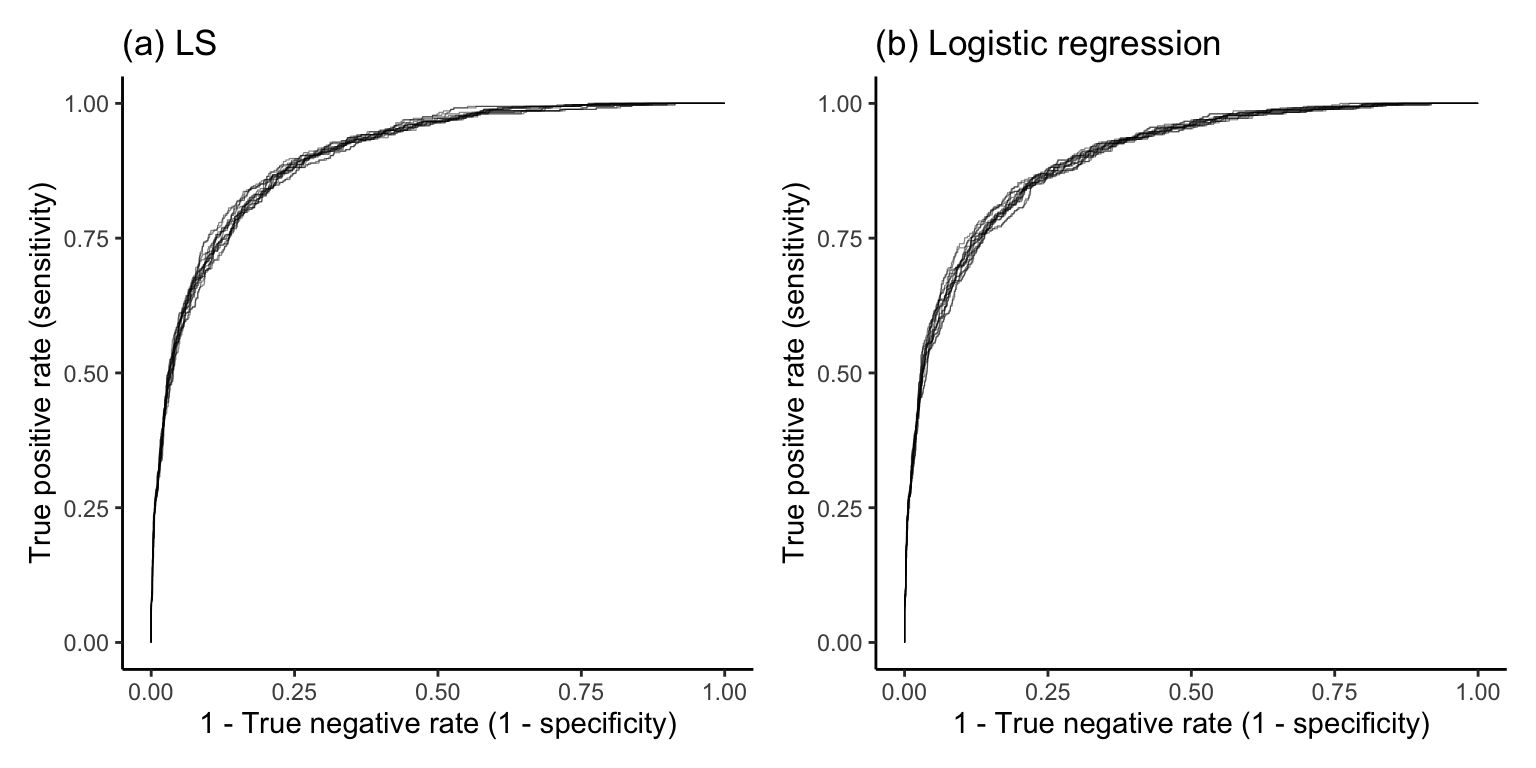

The code/documentation for conducting these PCS evaluations can be found in the 03_prediction_logistic.qmd (or .ipynb) file in the online_shopping/dslc_documentation/ subfolder of the online GitHub repository.
Exercises
True or False Exercises
For each question, specify whether the answer is true or false (briefly justify your answers).
Although the LS algorithm is designed for continuous response prediction problems, it can also be used for binary response prediction problems.
The unthresholded predictions computed by the LS algorithm for a binary response correspond to the predicted probability of being in the positive class.
Many continuous response problems can be translated into binary response problems.
The logistic transformation can be used to transform a linear combination of predictive features into a predicted positive class probability.
The logistic regression loss can be minimized using LS and has a unique “closed form” solution.
We cannot conduct a stability analysis for binary prediction problems because the response variable has only two values.
In medicine, it is always more important to have a high true positive rate (sensitivity) than it is to have a high true negative rate (specificity).
For a binary predictive algorithm that always predicts the positive class, the sensitivity of the algorithm evaluated on the validation set will be equal to the proportion of training data points in the positive class.
If algorithm A has a higher AUC than algorithm B, then algorithm A will achieve better prediction accuracy than algorithm B for every choice of probability threshold value.
Creating binary predictions using a probability prediction threshold value equal to the proportion of observations in the positive class is often a better choice than a threshold value of 0.5.
The logistic regression algorithm requires that the predictive features have a Gaussian distribution.
Conceptual Exercises
Explain how you could use the continuous response LS algorithm to generate predictions of a binary response. Why do you think that this is not commonly done in practice?
Why does prediction accuracy alone not necessarily provide a complete picture of an algorithm’s prediction performance?
In your own words, define the true positive rate (sensitivity) and the true negative rate (specificity).
Suppose that you are developing an algorithm to predict whether a user will click on a particular advertisement based on their online behavior.
What do sensitivity and specificity mean in the context of this problem?
Do you think that it makes more sense to prioritize high sensitivity or high specificity for this problem? Explain your reasoning.
Suppose that you are developing an algorithm to predict whether a patient is at high risk of lung cancer. Patients predicted to be at high risk are then entered into a regimen in which they undergo a highly invasive lung biopsy regimen every two years to detect whether they have developed lung cancer.
What do sensitivity and specificity mean in the context of this problem?
Do you think that it makes more sense to prioritize high sensitivity or high specificity for this problem?
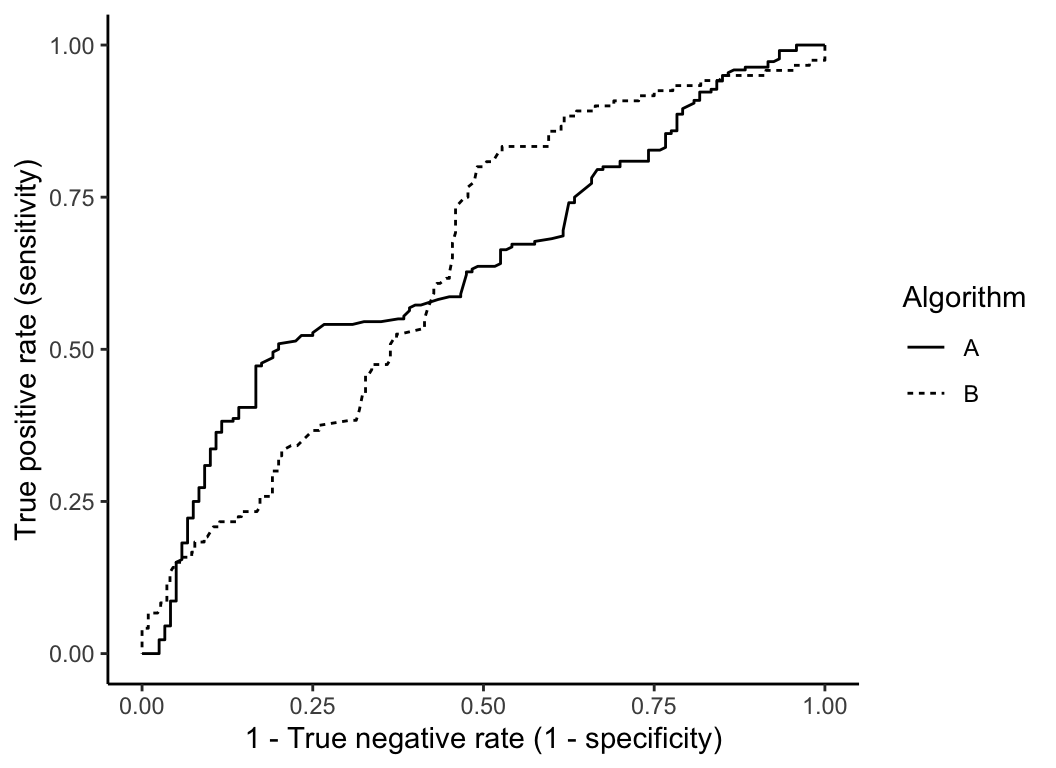
The following graph shows ROC curves for two algorithms, A and B, both of which have the same AUC. If you were prioritizing high true positive rate (sensitivity) performance over high true negative rate (specificity) performance, which algorithm would you choose?
Mathematical Exercises
For this exercise, you will show why logistic regression is considered to be a “linear classifier”. Suppose that you have trained a logistic regression fit with two features (\(x_1\) and \(x_2\)) and that you are using a threshold of \(0.5\) to convert your probability predictions to binary predictions. Show that the “decision boundary” (the point at which the binary predictions change from being 0 to being 1) is a linear combination of the predictors by demonstrating that the predicted positive class probability (\(\frac{1}{1 + e^{-(b_0 + b_1 x_1 + b_2 x_2)}}\)) equals \(0.5\) precisely when \(b_0 + b_1x_1 + b_2x_2 = 0\).
Show that logistic regression probability predictions (\(p = \frac{1}{1 + e^{-(b_0 + b_1 x)}}\)) are bounded between 0 and 1.
Suppose that you have trained a logistic regression fit for predicting whether a patient has an elevated risk of ovarian cancer (positive class) or not (negative class) based on two predictive features corresponding to the expression levels of two genes (\(\textrm{gene}_1\) and \(\textrm{gene}_2\)). The predictive fit takes the following form \[p = \frac{1}{1 + e^{-1.33 + 5.2\textrm{gene}_1 - 1.7\textrm{gene}_2}}\] The gene expression measurements for the three patients are \((\textrm{gene}_1, \textrm{gene}_2) = (5, 12)\), \((\textrm{gene}_1, \textrm{gene}_2) = (4, 12)\), and \((\textrm{gene}_1, \textrm{gene}_2) = (4, 10)\). Use this logistic regression fit to predict whether each of the three patients has an elevated risk of ovarian cancer using a probability threshold of 0.5.
This exercise compares the continuous response performance measures with the binary response performance measures.
Show that the mean squared error (MSE) computed for binary responses equals the prediction error.
Show that the mean absolute error (MAE) computed for binary responses also equals the prediction error.
Show that the median absolute deviation (MAD) computed for binary responses is not equal to the prediction error.
The following table shows a confusion matrix for a general positive/negative class prediction problem in terms of numbers \(a\), \(b\), \(c\), and \(d\). Write formulas for the prediction accuracy, prediction error, true positive rate, and true negative rate in terms of \(a\), \(b\), \(c\), and \(d\).
Predicted positive Predicted negative Observed positive a b Observed negative c d The following table provides a confusion matrix for a binary prediction problem.
Predicted positive Predicted negative Observed positive 122 8 Observed negative 59 205 Compute the prediction accuracy, prediction error, true positive rate, and true negative rate.
The following table provides another confusion matrix based on a different algorithm used to generate alternative predictions for the same data. Compute the prediction accuracy, prediction error, true positive rate, and true negative rate.
Predicted positive Predicted negative Observed positive 107 23 Observed negative 50 214 Comment on the difference in performance of the two algorithms.
Coding Exercises
Conduct some of your own exploratory and explanatory data analysis of the online shopping data in the
02_eda.qmd(or.ipynb) file in theonline_shopping/dslc_documentation/subfolder of the supplementary GitHub repository.Run through the binary prediction code in the
03_prediction_logistic.qmd(or.ipynb) file in theonline_shopping/dslc_documentation/subfolder of the supplementary GitHub repository. Add a section to this file in which you conduct some additional explorations of at least one predictive fit that is created in this file.
Project Exercises
Predicting house affordability in Ames The goal of this exercise is to predict the “affordability’’ (a binarization of the sale price response) of houses in Ames, Iowa, based on the dataset that was used in the continuous response prediction problem. Complete this project in a new DSLC code file in the
ames_houses/dslc_documentation/folder on the supplementary GitHub repository.Using the default version of the cleaned and preprocessed data (stored in the object called
ames_train_preprocessed, which is loaded/sourced in the first code chunk of each of the prediction files), convert the continuous Ames house price response variable into a binary response variable based on whether each house will sell within your budget (under $165,000) or will be out of your price range (over $165,000).Train LS and logistic regression algorithms using this training dataset to predict the binary house affordability response that you just created. Your fits should involve all remaining variables as the predictive features (remember to remove the original sale price variable).
Use the relevant validation set to evaluate the predictability of your fits. Which algorithm seems to generate more accurate predictions? Remember to use multiple measures of predictive performance (i.e., not just accuracy).
Conduct a stability analysis of your predictive performance (investigate both data perturbations as well as cleaning and judgment call perturbations).
Identify which features are the most important predictive features for each algorithm by comparing the standardized coefficients. You can do this by either (i) standardizing the coefficients using a bootstrapped estimate of the SD or (ii) standardizing the predictive features before training the algorithms.
Filter your training data to keep just the top 20 percent of the most expensive houses and the bottom 20 percent of the least expensive houses (based on the original unthresholded sale price variable). Retrain your LS and logistic regression algorithms and repeat the variable importance analysis from step (e) for this smaller training dataset where the two classes (affordable and not affordable) are substantially more different from one another. Compare with your previous results.
Repeat the previous step, this time keeping just the top 25 percent of the most expensive houses and the bottom 25 percent of the least expensive houses (based on the original unthresholded sale price variable). Retrain your LS and logistic regression algorithms and repeat the variable importance analysis. Do your conclusions change? Comment on the stability of the variable importance results based on the findings from parts (e), (f), and (g).
Predicting patients at risk of diabetes In this project, your goal is to generate a binary prediction algorithm that can predict when a patient is at risk of diabetes. You will be using data collected from the 2016 release of the National Health and Nutrition Examination Survey (NHANES), a program of studies designed to assess the health and nutritional status of adults and children in the United States. The relevant files for this project can be found in the
exercises/diabetes_nhanes/subfolder of the GitHub repository.The
exercises/diabetes_nhanes/data/folder contains the entire 2016 NHANES dataset (samadult.csv), which has over 800 columns and around 23,500 rows. TheloadDiabetesData.R(or.py) file in the relevantdslc_documentation/functions/subfolder contains some code for creating a simplified version of the NHANES data with just 11 predictive features, a diabetes response variable, and a person ID variable.Conduct some research into the NHANES data and summarize the relevant background information—including the data collection mechanism—in the data cleaning
01_cleaning.qmd(or.ipynb) file in thedslc_documentation/subfolder. A good place to start is the data documentation provided with the data and the NHANES website.Split the data into training, validation, and test sets, and justify your splitting procedure choice. You may want to save your code in a script called
prepareDiabetesData.R(or.py) in the subfolderdslc_documentation/functions/subfolder.In the
01_cleaning.qmd(or.ipynb) file in thedslc_documentation/subfolder, conduct some data cleaning explorations. You may use the simplified version that we created in theloadDiabetesData.R(or.py) file or any other version of the data that you prefer (don’t forget to take note of judgment calls, and remember that you can include them as arguments in your cleaning/preprocessing functions). Write a cleaning/preprocessing data preparation function that you can use to clean and preprocess the data in your EDA and prediction files. You may want to save this function in the sameprepareDiabetesData.R(or.py) file (in thedslc_documentation/functions/subfolder) in which you conducted your train/val/test data split.Conduct an EDA of the data in the
02_eda.qmd(or.ipynb) file in thedslc_documentation/subfolder. Be sure to create at least one explanatory figure. You may want (but are not required) to use principal component analysis and clustering techniques to explore the data.In the
03_prediction.qmd(or.ipynb) file in the relevantdslc_documentation/subfolder, generate some predictive fits for predicting diabetes status by training the LS and logistic regression algorithms using the training data.Conduct a thorough PCS analysis of each of your algorithmic fits (at the end of the
03_prediction.qmdor.ipynbfile in the relevantdslc_documentation/subfolder). Your PCS analysis should involve evaluating your predictions on the validation set, and investigating the stability of your predictions to data perturbations and cleaning and preprocessing judgment calls.
References
This variable was originally called “Revenue,” but we changed it to “purchase” for clarity.↩︎
This would not be an issue if we had multiple years of data, since then we could create a training dataset that spanned the entire yearly cycle using a time-based split.↩︎
Note that you can use different numbers to numerically encode the binary variables, such as \(1\) and \(2\), but \(0\) and \(1\) is the most common choice for binary encoding.↩︎
You probably already have some basic intuition for what a probability is. For example, if someone said “The probability that this session will end in a purchase is \(0.2\) (or \(20\) percent),” you probably have some kind of vague sense of what that means. In this book, we won’t dwell on the technical definitions of probabilities, so feel free to think in terms of your intuitive probabilistic understanding.↩︎
While there is no closed algebraic formula for the minima, the log-loss function is convex, so an optimal set of coefficients does exist in general.↩︎
Notice that the set of individual observations whose responses are correctly/incorrectly predicted by each algorithm are not the same. So, while two algorithms may look the same when their performance is viewed in aggregate, there may be significant underlying differences in the individual predictions.↩︎
This terminology is based on the fact that the classes are commonly encoded as \(-1\) and \(1\) (rather than \(0\) and \(1\)). In this book, while we will use the terminology “positive” and “negative” class, we will stick with the \(0\) and \(1\) encoding.↩︎